Двоичная арифметика
Правила выполнения арифметических действий очень просты. Они задаются таблицами сложения, вычитания и умножения (см.таблицу 2).
Таблица 2 - Правила представления арифметических операций
Таблицы |
||
Двоичное сложение |
Двоичное вычитание |
Двоичное умножение |
0 + 0 = 0 |
0 – 0 = 0 |
0 x 0 = 0 |
1 + 0 = 1 |
1 – 0 = 1 |
1 x 0 = 0 |
0 + 1 = 1 |
1 – 1 = 0 |
0 x 1 = 0 |
1 + 1 = 10 |
10 – 1 = 1 |
1 x 1 = 1 |
При сложении двух чисел, равных 1, в данном разряде получается 0, а 1 переносится в старший разряд.
Пример: Даны числа 101(2) и 11(2). Найти сумму этих чисел.
,
где 101(2)= 5(10), 11(2)= 3(10), 1000(2) = 8(10).
Проверка: 5+3=8.
При вычитании из 0 единицы, занимается единица из старшего ближайшего разряда, отличного от 0. При этом единица, занятая в старшем разряде, даёт 2 единицы в младшем разряде и по единице во всех разрядах между старшим и младшим.
Пример: Даны числа 101(2) и 11(2). Найти разность этих чисел.
,
где 101(2)=5(10), 11(2)=3(10), 10(2)=2(10).
Проверка: 5-3=2.
Операция умножения сводится к многократному сдвигу и сложению.
Пример: Даны числа 11(2) и 10(2). Найти произведение этих чисел.
11
*10
00
11
110,
где: 11(2)=3(10), 10(2)=2(10), 110(2)=6(10). Проверка: 3*2=6.
Правила арифметики во всех позиционных системах аналогичны (10 с/с, 2 с/с, 8 с/с и 16 с/с). Поэтому действия над двоичными числами производятся подобно сложению, вычитанию, умножению и делению целых, дробных десятичных и смешанных чисел в 10 с/с в соответствии с таблицей 2.
Благодаря простой двоичной арифметике при работе в 2 с/с упрощаются схемы арифметических устройств.
Запись первых двух десятков чисел в системах счисления представлена в таблице 3.
Таблица 3 - Представление чисел в системах счисления
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
0 |
0000 |
0 |
0 |
1 |
0001 |
1 |
1 |
2 |
0010 |
2 |
2 |
3 |
0011 |
3 |
3 |
4 |
0100 |
4 |
4 |
5 |
0101 |
5 |
5 |
6 |
0110 |
6 |
6 |
7 |
0111 |
7 |
7 |
8 |
1000 |
10 |
8 |
9 |
1001 |
11 |
9 |
10 |
1010 |
12 |
А |
11 |
1011 |
13 |
B |
12 |
1100 |
14 |
C |
13 |
1101 |
15 |
D |
14 |
1110 |
16 |
E |
15 |
1111 |
17 |
F |
16 |
10000 |
20 |
10 |
17 |
10001 |
21 |
11 |
18 |
10010 |
22 |
12 |
19 |
10011 |
23 |
13 |
20 |
10100 |
24 |
14 |
Перевод чисел из любой системы счисления в десятичную
Пример: Дано число 11012. Необходимо перевести число 11012 из двоичной системы счисления в десятичную систему счисления.
Решение:
1.Для перевода числа из любой системы счисления в десятичную, необходимо разложить это число по степеням основания этой системы:
1101(2) = 13120110(2)
2.Каждую цифру числа умножить на основание, возведенное в соответствующую степень:
13120110(2)=1*23+1*22+0*21+1*20=8+4+0+1=13(10)
3.Число 11012=13(10)
Примечание: При переводе важно помнить, что любое число в нулевой степени равно 1.
Пример: Дано число 134. Необходимо перевести число 134 из четверичной системы счисления в десятичную систему счисления.
Решение:
1. Для перевода числа из любой системы счисления в десятичную систему, необходимо разложить это число по степеням основания этой системы:
13(4) = 1130(4)
2. Каждую цифру числа умножить на основание, возведенное в соответствующую степень:
1130(4)=1*41+3*40=4+3=7(10)
3. Число 13(4)=7(10)
Перевод чисел из десятичной системы счисления в любую другую
Пример: Дано число 1310. Необходимо перевести число 1310 из десятичной системы счисления в двоичную систему счисления.
Решение:
1.Для перевода чисел из десятичной системы счисления в любую другую, необходимо делить десятичное число на основание системы, в которую переводят, сохраняя при этом остатки от каждого деления. Деление продолжается до тех пор, пока результат деления не станет меньше делителя.
13/2=6 (остаток 1), т.к. частное 6 больше делителя 2, то продолжаем делить частное 6 на 2.
6/2=3 (остаток 0), т.к. частное 3 больше делителя 2, то продолжаем делить частное 3 на 2.
3/2=1 (остаток 1), т.к. частное 1 меньше делителя 2, то записываем полученное число.
13(10) = 1101(2).
2.Результат формируем справа налево (при формировании числа используют остатки при делении).
1101(2).
Пример: Дано число 710. Необходимо перевести число 710 из десятичной системы счисления в четверичную систему счисления.
Решение:
1.Для перевода чисел из десятичной системы счисления в любую другую, необходимо делить десятичное число на основание системы, в которую переводят, сохраняя при этом остатки от каждого деления. Деление продолжается до тех пор, пока результат деления не станет меньше делителя.
7/4=1 (остаток 3), т.к. частное 1 меньше делителя 4, то записываем полученное число.
4
3
7
4
1
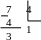
7(10) = 13(4).
2.Результат формируем справа налево (при формировании числа использу- ют остатки при делении).
13(4).