1 Вариант

1. Центр окружности, диаметр которой равен 10 см, удален от прямых АВ и ВС, содержащих стороны параллелограмма АВСД, на 4 см и 5 см соответственно. Какая из прямых АВ или ВС имеет с окружностью две общие точки?

2. Из точки А к окружности проведены две касательные АВ и АС, где В и С – точки касания. Через точку Д этой окружности проведена ещё одна касательная, которая пересекает лучи АВ и АС в точках F и Т соответственно. Вычислите длину отрезка FТ, если известно, что ВF=ТС=2 см.

3. Окружность с центром в точке О касается сторон АВ,ВС и АД прямоугольной трапеции АВСД. Точка Р- точка касания окружности и стороны ВС, ОР= 6 см, ВС=14 см. Вычислите расстояние между точками О и С.

4. Из точки А к окружности, центром которой является точка О, проведена касательная, F- точка касания. Отрезок АО пересекает окружность в точке Т. Отрезок ТF является медианой треугольника АОF. Вычислите длину отрезка касательной, если ТF=3 см.

Самостоятельная работа «Центральные и вписанные углы» (9 класс) 1 вариант

1. На рисунке точки А,В,С и F лежат на окружности, центром которой является точка О. Какое из равенств является верным: а) ВАС = ВС; б) ВОF = ВС; в) ВОС = ВС.

2. Вершины трапеции АВСД лежат на окружности. Верно ли, что ∠АСД =∠АВД? Ответ поясните.

3. Вершины А, В, Д параллелограмма АВСД лежат на окружности с центром в точке О, О АД. Вычислите градусные меры углов параллелограмма, если известно, что ∠ ВОД = 100⁰.

4. Окружность касается стороны АД прямоугольника АВСД в точке Р. Вычислите градусную меру угла АВР, если ∪ ОТР:∪ ОFР=1:2.

5. Отрезок АВ – диаметр окружности с центром в точке О и радиусом 2 см. Прямая 𝓁 касается окружности в точке С и пересекает луч АВ в точке Р. Вычислите площадь треугольника РСВ, если ∠СРВ = 30⁰.

Самостоятельная работа «Центральные и вписанные углы» (9 класс) 2 вариант

1. На рисунке точки А,В,С лежат на окружности, центром которой является точка О( О АВ). Какое из равенств является верным: а) АОС = АС; б) АВД = АС; в) АДВ = АВ.

2. Вершины четырёхугольника АВСД лежат на окружности. Верно ли, что ∠АСД =∠АВД? Ответ поясните.

3. Вершины В и С треугольника СОВ лежат на окружности, центром которой является точка О. Луч СО пересекает окружность в точке А. Вычислите градусные меры углов треугольника СОВ, если известно, что ∪ АВ = 60⁰.

4. Окружность касается стороны АД параллелограмма АВСД в точке Р. Вычислите градусную меру угла АВР, если известно, что ∪ ОFР - ∪ ОТР=120⁰ и АВ = ВР.

5. Отрезок АС – диаметр окружности с центром в точке О . Прямая 𝓁 касается окружности в точке В и пересекает луч АС в точке К. Вычислите площадь треугольника АВК, если ∠АВК = 120⁰ и АС = 6 см.

Самостоятельная работа «Центральные и вписанные углы» (9 класс) 1 вариант

1. На рисунке точки А,В,С и F лежат на окружности, центром которой является точка О. Какое из равенств является верным: а) ВАС = ВС; б) ВОF = ВС; в) ВОС = ВС.

2. Вершины трапеции АВСД лежат на окружности. Верно ли, что ∠АСД =∠АВД? Ответ поясните.

3. Вершины А, В, Д параллелограмма АВСД лежат на окружности с центром в точке О, О АД. Вычислите градусные меры углов параллелограмма, если известно, что ∠ ВОД = 100⁰.

4. Окружность касается стороны АД прямоугольника АВСД в точке Р. Вычислите градусную меру угла АВР, если ∪ ОТР:∪ ОFР=1:2.

5. Отрезок АВ – диаметр окружности с центром в точке О и радиусом 2 см. Прямая 𝓁 касается окружности в точке С и пересекает луч АВ в точке Р. Вычислите площадь треугольника РСВ, если ∠СРВ = 30⁰.

Самостоятельная работа «Центральные и вписанные углы» (9 класс) 2 вариант

1. На рисунке точки А,В,С лежат на окружности, центром которой является точка О( О АВ). Какое из равенств является верным: а) АОС = АС; б) АВД = АС; в) АДВ = АВ.

2. Вершины четырёхугольника АВСД лежат на окружности. Верно ли, что ∠АСД =∠АВД? Ответ поясните.

3. Вершины В и С треугольника СОВ лежат на окружности, центром которой является точка О. Луч СО пересекает окружность в точке А. Вычислите градусные меры углов треугольника СОВ, если известно, что ∪ АВ = 60⁰.

4. Окружность касается стороны АД параллелограмма АВСД в точке Р. Вычислите градусную меру угла АВР, если известно, что ∪ ОFР - ∪ ОТР=120⁰ и АВ = ВР.

5. Отрезок АС – диаметр окружности с центром в точке О . Прямая 𝓁 касается окружности в точке В и пересекает луч АС в точке К. Вычислите площадь треугольника АВК, если ∠АВК = 120⁰ и АС = 6 см.

Самостоятельная работа «Центральные и вписанные углы» (9 класс) 1 вариант

1. На рисунке точки А,В,С и F лежат на окружности, центром которой является точка О. Какое из равенств является верным: а) ВАС = ВС; б) ВОF = ВС; в) ВОС = ВС.

2. Вершины трапеции АВСД лежат на окружности. Верно ли, что ∠АСД =∠АВД? Ответ поясните.

3. Вершины А, В, Д параллелограмма АВСД лежат на окружности с центром в точке О, О АД. Вычислите градусные меры углов параллелограмма, если известно, что ∠ ВОД = 100⁰.

4. Окружность касается стороны АД прямоугольника АВСД в точке Р. Вычислите градусную меру угла АВР, если ∪ ОТР:∪ ОFР=1:2.

5. Отрезок АВ – диаметр окружности с центром в точке О и радиусом 2 см. Прямая 𝓁 касается окружности в точке С и пересекает луч АВ в точке Р. Вычислите площадь треугольника РСВ, если ∠СРВ = 30⁰.

Самостоятельная работа «Центральные и вписанные углы» (9 класс) 2 вариант

1. На рисунке точки А,В,С лежат на окружности, центром которой является точка О( О АВ). Какое из равенств является верным: а) АОС = АС; б) АВД = АС; в) АДВ = АВ.

2. Вершины четырёхугольника АВСД лежат на окружности. Верно ли, что ∠АСД =∠АВД? Ответ поясните.

3. Вершины В и С треугольника СОВ лежат на окружности, центром которой является точка О. Луч СО пересекает окружность в точке А. Вычислите градусные меры углов треугольника СОВ, если известно, что ∪ АВ = 60⁰.

4. Окружность касается стороны АД параллелограмма АВСД в точке Р. Вычислите градусную меру угла АВР, если известно, что ∪ ОFР - ∪ ОТР=120⁰ и АВ = ВР.

5. Отрезок АС – диаметр окружности с центром в точке О . Прямая 𝓁 касается окружности в точке В и пересекает луч АС в точке К. Вычислите площадь треугольника АВК, если ∠АВК = 120⁰ и АС = 6 см.

Контрольная работа «Квадратные неравенства» (9 класс) 1 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² х т.е. все х

б) х² , нет решений;

в) х²+3 0, нет решений;

г) х² -4, х-любое число, т.е. все х

2 уровень. 2) Какие из чисел: -3; 0; 1; 4 принадлежат множеству решений неравенства 3х² – 2х -4

3 уровень. 3) Решите неравенство: 1) 2х²+5х - 7 ; 2) 9х² – 6х + 1 3) (х-1)(х+3)(х²-25)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²-2х-3

х²-11х+28

5 уровень. 5) Решите неравенство:

Контрольная работа «Квадратные неравенства» (9 класс) 2 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х²

б) х² , х-любое число, т.е. все х

в) х² , нет решений;

г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -2; 0; -1; 6 принадлежат множеству решений неравенства х² +3х +1

3 уровень. 3) Решите неравенство: 1) 2х²+5х - 3 ; 2) 25х² +10х + 1 3) (х+4)(х-7)(х²-64)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²+х-6

-х²- х+2

5 уровень. 5) Решите неравенство:

Контрольная работа «Квадратные неравенства» (9 класс) 1 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² х т.е. все х

б) х² , нет решений;

в) х²+3 0, нет решений;

г) х² -4, х-любое число, т.е. все х

2 уровень. 2) Какие из чисел: -3; 0; 1; 4 принадлежат множеству решений неравенства 3х² – 2х -4

3 уровень. 3) Решите неравенство: 1) 2х²+5х - 7 ; 2) 9х² – 6х + 1 3) (х-1)(х+3)(х²-25)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²-2х-3

х²-11х+28

5 уровень. 5) Решите неравенство:

Контрольная работа «Квадратные неравенства» (9 класс) 2 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х²

б) х² , х-любое число, т.е. все х

в) х² , нет решений;

г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -2; 0; -1; 6 принадлежат множеству решений неравенства х² +3х +1

3 уровень. 3) Решите неравенство: 1) 2х²+5х - 3 ; 2) 25х² +10х + 1 3) (х+4)(х-7)(х²-64)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²+х-6

-х²- х+2

5 уровень. 5) Решите неравенство:

Домашняя контрольная работа «Квадратные неравенства» (9 класс) 3 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² б) х² , х-любое число, т.е. все х

в) х² , нет решений; г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -3; 0; -1; 4 принадлежат множеству решений неравенства х² +3х +1

3 уровень. 3) Решите неравенство: 1) 4х²-2х +13 ; 2) -2х² +6х -9 3) (2х-3)(х+2)(х-4)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²-4х+5

2х²+3х-9

5 уровень. 5) Решите неравенство:

Домашняя контрольная работа «Квадратные неравенства» (9 класс) 4 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² б) х² нет решений;

в) х² , нет решений; г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -7; 0; -3; -4 принадлежат множеству решений неравенства -2х² -8х-8

3 уровень. 3) Решите неравенство: 1) 5х²+2х +9 ; 2) 6х-9-х² 3) (3х+5)(х-2)(х+1)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²+4х-5

х²-6х+8

5 уровень. 5) Решите неравенство:

Домашняя контрольная работа «Квадратные неравенства» (9 класс) 3 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² б) х² , х-любое число, т.е. все х

в) х² , нет решений; г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -3; 0; -1; 4 принадлежат множеству решений неравенства х² +3х +1

3 уровень. 3) Решите неравенство: 1) 4х²-2х +13 ; 2) -2х² +6х -9 3) (2х-3)(х+2)(х-4)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²-4х+5

2х²+3х-9

5 уровень. 5) Решите неравенство:

Домашняя контрольная работа «Квадратные неравенства» (9 класс) 4 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² б) х² нет решений;

в) х² , нет решений; г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -7; 0; -3; -4 принадлежат множеству решений неравенства -2х² -8х-8

3 уровень. 3) Решите неравенство: 1) 5х²+2х +9 ; 2) 6х-9-х² 3) (3х+5)(х-2)(х+1)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²+4х-5

х²-6х+8

5 уровень. 5) Решите неравенство:

Домашняя контрольная работа «Квадратные неравенства» (9 класс) 3 вариант

1 уровень. 1) В каких случаях верно записаны решения неравенства?

а) х² б) х² , х-любое число, т.е. все х

в) х² , нет решений; г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -3; 0; -1; 4 принадлежат множеству решений неравенства х² +3х +1

3 уровень. 3) Решите неравенство: 1) 4х²-2х +13 ; 2) -2х² +6х -9 3) (2х-3)(х+2)(х-4)

4 уровень. 4) а) Найдите естественную область определения выражения: ;

б) Решите систему неравенств: х²-4х+5

2х²+3х-9

5 уровень. 5) Решите неравенство:

1 уровень. 1) В каких случаях верно записаны решения неравенства? 4 вариант

а) х² б) х² нет решений;

в) х² , нет решений; г) х² , х т.е. все х

2 уровень. 2) Какие из чисел: -7; 0; -3; -4 принадлежат множеству решений неравенства -2х² -8х-8

3 уровень. 3) Решите неравенство: 1) 5х²+2х +9 ; 2) 6х-9-х² 3) (3х+5)(х-2)(х+1)

4 уровень. 4) а) Найдите естественную область определения выражения:

б) Решите систему неравенств: х²+4х-5

х²-6х+8 5 уровень. 5) Решите неравенство:

Вопросы к главе 1(п.1-3) 9 класс 1 вариант

1.Что называется касательной к окружности?

2. Сформулируйте признак касательной к окружности.

3. Какой угол называется центральным углом окружности?

4. Чему равна градусная мера вписанного в окружность угла?

5. Каким свойством обладают отрезки пересекающихся хорд окружности?

6. Каким свойством обладают точки биссектрисы угла треугольника?

7. Какие точки называются замечательными точками треугольника?

Вопросы к главе 1(п.1-3) 9 класс 2 вариант

1. Каким свойством обладает радиус окружности, проведенный в точку касания прямой и окружности?

2. Каким свойством обладают отрезки касательных к окружности, проведённых из одной точки?

3. Сформулируйте признак касания двух окружностей внешним образом.

4. Что называется градусной мерой дуги окружности?

5. Дайте определение вписанного в окружность угла.

6. Сформулируйте теорему об угле между хордой и касательной.

7. Сформулируйте теорему об отрезках секущей и касательной.

Вопросы к главе 1(п.1-3) 9 класс 1 вариант

1.Что называется касательной к окружности?

2. Сформулируйте признак касательной к окружности.

3. Какой угол называется центральным углом окружности?

4. Чему равна градусная мера вписанного в окружность угла?

5. Каким свойством обладают отрезки пересекающихся хорд окружности?

6. Каким свойством обладают точки биссектрисы угла треугольника?

7. Какие точки называются замечательными точками треугольника?

Вопросы к главе 1(п.1-3) 9 класс 2 вариант

1. Каким свойством обладает радиус окружности, проведенный в точку касания прямой и окружности?

2. Каким свойством обладают отрезки касательных к окружности, проведённых из одной точки?

3. Сформулируйте признак касания двух окружностей внешним образом.

4. Что называется градусной мерой дуги окружности?

5. Дайте определение вписанного в окружность угла.

6. Сформулируйте теорему об угле между хордой и касательной.

7. Сформулируйте теорему об отрезках секущей и касательной.

Вопросы к главе 1(п.1-3) 9 класс 1 вариант

1.Что называется касательной к окружности?

2. Сформулируйте признак касательной к окружности.

3. Какой угол называется центральным углом окружности?

4. Чему равна градусная мера вписанного в окружность угла?

5. Каким свойством обладают отрезки пересекающихся хорд окружности?

6. Каким свойством обладают точки биссектрисы угла треугольника?

7. Какие точки называются замечательными точками треугольника?

Вопросы к главе 1(п.1-3) 9 класс 2 вариант

1. Каким свойством обладает радиус окружности, проведенный в точку касания прямой и окружности?

2. Каким свойством обладают отрезки касательных к окружности, проведённых из одной точки?

3. Сформулируйте признак касания двух окружностей внешним образом.

4. Что называется градусной мерой дуги окружности?

5. Дайте определение вписанного в окружность угла.

6. Сформулируйте теорему об угле между хордой и касательной.

7. Сформулируйте теорему об отрезках секущей и касательной.

Вопросы к главе 1(п.1-3) 9 класс 1 вариант

1.Что называется касательной к окружности?

2. Сформулируйте признак касательной к окружности.

3. Какой угол называется центральным углом окружности?

4. Чему равна градусная мера вписанного в окружность угла?

5. Каким свойством обладают отрезки пересекающихся хорд окружности?

6. Каким свойством обладают точки биссектрисы угла треугольника?

7. Какие точки называются замечательными точками треугольника?

Вопросы к главе 1(п.1-3) 9 класс 2 вариант

1. Каким свойством обладает радиус окружности, проведенный в точку касания прямой и окружности?

2. Каким свойством обладают отрезки касательных к окружности, проведённых из одной точки?

3. Сформулируйте признак касания двух окружностей внешним образом.

4. Что называется градусной мерой дуги окружности?

5. Дайте определение вписанного в окружность угла.

6. Сформулируйте теорему об угле между хордой и касательной.

7. Сформулируйте теорему об отрезках секущей и касательной.

Самостоятельная работа «Вписанные и описанные треугольники» (9 класс) 1 вариант

1. Хорды АВ и СД окружности пересекаются в точке О. Около какого из треугольников ВОС, АВД или ВОД описана окружность?

2. В треугольник АВС вписана окружность с центром в точке О и радиусом 2,8 см. Найдите площадь треугольника АОВ, если АВ=10,7 см.

3. Около прямоугольного треугольника описана окружность радиуса 10 см. Найдите периметр и площадь этого треугольника, если его катет равен 16 см.

4. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите длины катетов этого треугольника.

5. Точка Т принадлежит стороне ВС прямоугольника АВСД., АТ=АД и угол ВАТ= 30⁰. Вычислите радиус окружности, вписанной в треугольник АТД, если ВТ= 3 см.

Самостоятельная работа «Вписанные и описанные треугольники» (9 класс) 2 вариант

1. Хорды АВ и СД окружности пересекаются в точке О. Какой из треугольников АОС, АСВ или СОВ является вписанным в окружность?

2. В треугольник АВС вписана окружность с центром в точке О и радиусом 2,4 см. Найдите площадь треугольника ВОС, если ВС=12,7 см.

3. Около прямоугольного треугольника описана окружность радиуса 2,5 см. Найдите периметр и площадь этого треугольника, если его катет равен 4 см.

4. В прямоугольный треугольник, длина гипотенузы которого равна 13 см, вписана окружность. Найдите длины катетов этого треугольника, если радиус окружности равен 2 см..

5. Точки Р и Т принадлежат соответственно сторонам ВС и СД квадрата АВСД, причем ВР=ДТ и угол ВАР= 15⁰. Вычислите радиус окружности, вписанной в треугольник АРТ, если РТ= 12 см.

Самостоятельная работа «Вписанные и описанные треугольники» (9 класс) 1 вариант

1. Хорды АВ и СД окружности пересекаются в точке О. Около какого из треугольников ВОС, АВД или ВОД описана окружность?

2. В треугольник АВС вписана окружность с центром в точке О и радиусом 2,8 см. Найдите площадь треугольника АОВ, если АВ=10,7 см.

3. Около прямоугольного треугольника описана окружность радиуса 10 см. Найдите периметр и площадь этого треугольника, если его катет равен 16 см.

4. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите длины катетов этого треугольника.

5. Точка Т принадлежит стороне ВС прямоугольника АВСД., АТ=АД и угол ВАТ= 30⁰. Вычислите радиус окружности, вписанной в треугольник АТД, если ВТ= 3 см.

Самостоятельная работа «Вписанные и описанные треугольники» (9 класс) 2 вариант

1. Хорды АВ и СД окружности пересекаются в точке О. Какой из треугольников АОС, АСВ или СОВ является вписанным в окружность?

2. В треугольник АВС вписана окружность с центром в точке О и радиусом 2,4 см. Найдите площадь треугольника ВОС, если ВС=12,7 см.

3. Около прямоугольного треугольника описана окружность радиуса 2,5 см. Найдите периметр и площадь этого треугольника, если его катет равен 4 см.

4. В прямоугольный треугольник, длина гипотенузы которого равна 13 см, вписана окружность. Найдите длины катетов этого треугольника, если радиус окружности равен 2 см..

5. Точки Р и Т принадлежат соответственно сторонам ВС и СД квадрата АВСД, причем ВР=ДТ и угол ВАР= 15⁰. Вычислите радиус окружности, вписанной в треугольник АРТ, если РТ= 12 см.

Самостоятельная работа «Вписанные и описанные треугольники» (9 класс) 1 вариант

1. Хорды АВ и СД окружности пересекаются в точке О. Около какого из треугольников ВОС, АВД или ВОД описана окружность?

2. В треугольник АВС вписана окружность с центром в точке О и радиусом 2,8 см. Найдите площадь треугольника АОВ, если АВ=10,7 см.

3. Около прямоугольного треугольника описана окружность радиуса 10 см. Найдите периметр и площадь этого треугольника, если его катет равен 16 см.

4. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите длины катетов этого треугольника.

5. Точка Т принадлежит стороне ВС прямоугольника АВСД., АТ=АД и угол ВАТ= 30⁰. Вычислите радиус окружности, вписанной в треугольник АТД, если ВТ= 3 см.

Самостоятельная работа «Вписанные и описанные треугольники» (9 класс) 2 вариант

1. Хорды АВ и СД окружности пересекаются в точке О. Какой из треугольников АОС, АСВ или СОВ является вписанным в окружность?

2. В треугольник АВС вписана окружность с центром в точке О и радиусом 2,4 см. Найдите площадь треугольника ВОС, если ВС=12,7 см.

3. Около прямоугольного треугольника описана окружность радиуса 2,5 см. Найдите периметр и площадь этого треугольника, если его катет равен 4 см.

4. В прямоугольный треугольник, длина гипотенузы которого равна 13 см, вписана окружность. Найдите длины катетов этого треугольника, если радиус окружности равен 2 см..

5. Точки Р и Т принадлежат соответственно сторонам ВС и СД квадрата АВСД, причем ВР=ДТ и угол ВАР= 15⁰. Вычислите радиус окружности, вписанной в треугольник АРТ, если РТ= 12 см.

Самостоятельная работа «Системы линейных уравнений с двумя переменными» (9 класс) 1 вариант

1 уровень. 1)Из пар чисел (-1;8), (1;8), (-8;1) выберите решение системы уравнений:

2 уровень.2) Решите систему уравнений: а) б)

3 уровень.3) Решите систему уравнений: а) б) в)

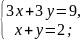4 уровень. 4) ) Решите систему уравнений: а) б) в)

г)

5 уровень. 5) При каких значениях а решением системы уравнений является упорядоченная пара отрицательных чисел:

Самостоятельная работа «Системы линейных уравнений с двумя переменными» (9 класс) 2 вариант

1 уровень. 1)Из пар чисел (-1;8), (1;8), (-8;1) выберите решение системы уравнений:

2 уровень.2) Решите систему уравнений: а) б)

3 уровень.3) Решите систему уравнений: а) б) в)

4 уровень. 4) ) Решите систему уравнений: а) б) в)

г)

5 уровень. 5) При каких значениях а решением системы уравнений является упорядоченная пара отрицательных чисел:

Самостоятельная работа «Системы линейных уравнений с двумя переменными» (9 класс) 1 вариант

1 уровень. 1)Из пар чисел (-1;8), (1;8), (-8;1) выберите решение системы уравнений:

2 уровень.2) Решите систему уравнений: а) б)

3 уровень.3) Решите систему уравнений: а) б) в)

4 уровень. 4) ) Решите систему уравнений: а) б) в)

г)

5 уровень. 5) При каких значениях а решением системы уравнений является упорядоченная пара отрицательных чисел:

Самостоятельная работа «Системы линейных уравнений с двумя переменными» (9 класс) 2 вариант

1 уровень. 1)Из пар чисел (-1;8), (1;8), (-8;1) выберите решение системы уравнений:

2 уровень.2) Решите систему уравнений: а) б)

3 уровень.3) Решите систему уравнений: а) б) в)

4 уровень. 4) ) Решите систему уравнений: а) б) в)

г)

5 уровень. 5) При каких значениях а решением системы уравнений является упорядоченная пара отрицательных чисел:

Контрольная работа «Вписанные и описанные многоугольники» (9 класс) 1 вариант

1 уровень. 1) В какой из данных четырёхугольников можно вписать окружность?

2 уровень.2) Радиус окружности, вписанной в равносторонний треугольник, равен 2 см. Вычислите периметр этого треугольника.

3 уровень. 3) Диагонали ромба АВСД пересекаются в точке О, ВО=6 см, ОС=10 см. Вычислите радиус окружности, описанной около треугольника ВОС.

4 уровень. 4) Найдите радиус окружности, описанной около треугольника, длины сторон которого – 10 см, 10 см, 12 см.

5 уровень. 5) В равнобедренную трапецию, длина боковой стороны которой 17 см, вписана окружность диаметром 15 см. Найдите длины оснований трапеции.

Контрольная работа «Вписанные и описанные многоугольники» (9 класс) 2 вариант

1 уровень. 1) Около какого из данных четырёхугольников можно описать окружность?

2 уровень.2) Радиус окружности, описанной около равностороннего треугольника, равен 4 см. Вычислите периметр этого треугольника.

3 уровень. 3) Диагонали ромба АВСД пересекаются в точке О. Радиус окружности, описанной около треугольника СОД, равен 5 см. Вычислите длину диагонали АС ромба, если известно, что ВО=6 см.

4 уровень. 4) Найдите радиус окружности, в которую вписан треугольник, длины сторон которого – 15 см, 15 см, 24 см.

5 уровень. 5) Равнобедренная трапеция с боковой стороной, равной 18 см, и углом при основании 60⁰описана около круга. Найдите длины оснований трапеции.

Контрольная работа «Вписанные и описанные многоугольники» (9 класс) 1 вариант

1 уровень. 1) В какой из данных четырёхугольников можно вписать окружность?

2 уровень.2) Радиус окружности, вписанной в равносторонний треугольник, равен 2 см. Вычислите периметр этого треугольника.

3 уровень. 3) Диагонали ромба АВСД пересекаются в точке О, ВО=6 см, ОС=10 см. Вычислите радиус окружности, описанной около треугольника ВОС.

4 уровень. 4) Найдите радиус окружности, описанной около треугольника, длины сторон которого – 10 см, 10 см, 12 см.

5 уровень. 5) В равнобедренную трапецию, длина боковой стороны которой 17 см, вписана окружность диаметром 15 см. Найдите длины оснований трапеции.

Контрольная работа «Вписанные и описанные многоугольники» (9 класс) 2 вариант

1 уровень. 1) Около какого из данных четырёхугольников можно описать окружность?

2 уровень.2) Радиус окружности, описанной около равностороннего треугольника, равен 4 см. Вычислите периметр этого треугольника.

3 уровень. 3) Диагонали ромба АВСД пересекаются в точке О. Радиус окружности, описанной около треугольника СОД, равен 5 см. Вычислите длину диагонали АС ромба, если известно, что ВО=6 см.

4 уровень. 4) Найдите радиус окружности, в которую вписан треугольник, длины сторон которого – 15 см, 15 см, 24 см.

5 уровень. 5) Равнобедренная трапеция с боковой стороной, равной 18 см, и углом при основании 60⁰описана около круга. Найдите длины оснований трапеции.

Контрольная работа «Вписанные и описанные многоугольники» (9 класс) 1 вариант

1 уровень. 1) В какой из данных четырёхугольников можно вписать окружность?

2 уровень.2) Радиус окружности, вписанной в равносторонний треугольник, равен 2 см. Вычислите периметр этого треугольника.

3 уровень. 3) Диагонали ромба АВСД пересекаются в точке О, ВО=6 см, ОС=10 см. Вычислите радиус окружности, описанной около треугольника ВОС.

4 уровень. 4) Найдите радиус окружности, описанной около треугольника, длины сторон которого – 10 см, 10 см, 12 см.

5 уровень. 5) В равнобедренную трапецию, длина боковой стороны которой 17 см, вписана окружность диаметром 15 см. Найдите длины оснований трапеции.

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 1 вариант

1 уровень.1) Найдите расстояние между точками А(2) и В(-3) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в точке (3;-2) и радиусом 7.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(2;3), В(3;4), А₁(4;7), В₁(5;6).

4 уровень.4) Докажите, что уравнение х²+2х+у²+4у-15=0 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(3;5),

С(-1;3), О(0;2).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 2 вариант

1 уровень.1) Найдите расстояние между точками А(8) и В(-1) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в начале координат и радиусом 1,5.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(1;4), В(2;3), А₁(4;5), В₁(6;1).

4 уровень.4) Докажите, что уравнение х²-10х+у²+2у+10=0 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(-2;6),

С(4;2), О(4;0).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 3 вариант

1 уровень.1) Найдите расстояние между точками А(-1) и В(-2) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в точке(-4;3) и радиусом 3.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(3;2), В(4;3), А₁(7;4), В₁(6;5).

4 уровень.4) Докажите, что уравнение х²-2х+у²-20у+97=0 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(5;3),

С(1;-3), О(0;4).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 4 вариант

1 уровень.1) Найдите расстояние между точками А(-4) и В(6) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в точке(-6;0) и радиусом 3.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(4;1), В(3;2), А₁(5;4), В₁(1;6).

4 уровень.4) Докажите, что уравнение х²+12х+у²+10у=-60 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(4;-6),

С(2;4), О(2;0).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 1 вариант

1 уровень.1) Найдите расстояние между точками А(2) и В(-3) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в точке (3;-2) и радиусом 7.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(2;3), В(3;4), А₁(4;7), В₁(5;6).

4 уровень.4) Докажите, что уравнение х²+2х+у²+4у-15=0 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(3;5),

С(-1;3), О(0;2).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 2 вариант

1 уровень.1) Найдите расстояние между точками А(8) и В(-1) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в начале координат и радиусом 1,5.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(1;4), В(2;3), А₁(4;5), В₁(6;1).

4 уровень.4) Докажите, что уравнение х²-10х+у²+2у+10=0 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(-2;6),

С(4;2), О(4;0).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 3 вариант

1 уровень.1) Найдите расстояние между точками А(-1) и В(-2) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в точке(-4;3) и радиусом 3.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(3;2), В(4;3), А₁(7;4), В₁(6;5).

4 уровень.4) Докажите, что уравнение х²-2х+у²-20у+97=0 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(5;3),

С(1;-3), О(0;4).

Самостоятельная работа «Расстояние между точками. Уравнение окружности» (9 класс) 4 вариант

1 уровень.1) Найдите расстояние между точками А(-4) и В(6) на координатной прямой.

2 уровень.2) Составьте уравнение окружности с центром в точке(-6;0) и радиусом 3.

3 уровень.3)Какой из отрезков больше АВ или А₁В₁, если А(4;1), В(3;2), А₁(5;4), В₁(1;6).

4 уровень.4) Докажите, что уравнение х²+12х+у²+10у=-60 есть уравнение окружности. Найдите координаты центра окружности и ее радиус.

5 уровень.5) У параллелограмма АВСД диагонали пересекаются в точке О. Найдите координаты точек А и Д, если В(4;-6),

С(2;4), О(2;0).

Самостоятельная работа “Использование систем уравнений при решении текстовых задач” (9 класс) 1 вариант

1) Найдите два натуральных числа, сумма которых равна 15, а разность равна 9.

2) В двузначном числе сумма цифр равна 12. Цифра десятков в три раза больше цифры единиц. Найдите это число.

3) Количество метров в первом куске ситца вдвое больше, чем во втором. Если от каждого из них отрезать по 13 м, то в первом куске будет в 2,5 раза больше ткани, чем во втором. Сколько метров ситца было первоначально в каждом куске?

4)Двое рабочих выполнили некоторую работу за 12 ч. Если бы сначала первый сделал половину этой работы, а затем второй- остальную её часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

5) Если двузначное число разделить на сумму его цифр, то в частном получится 7 и в остатке 6. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке число, равное сумме цифр исходного числа. Найдите исходное число.

Самостоятельная работа “Использование систем уравнений при решении текстовых задач” (9 класс) 2 вариант

1) Найдите два натуральных числа,одно из которых вдвое больше другого, а сумма этих чисел равна 18.

2) В двузначном натуральном числе сумма цифр равна 14. Цифра десятков на 4 больше цифры единиц. Найдите это число.

3) Длина гипотенузы прямоугольного треугольника равна 125 см, а сумма длин его катетов 175 см. Найдите длины катетов.

4)Двое рабочих выполнили некоторую работу за 6 ч. Если бы сначала первый сделал половину этой работы, а затем второй- остальную её часть, то вся работа была бы выполнена за 12,5 ч. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

5) Если двузначное число разделить на сумму его цифр, то в частном получится 4 и в остатке 3. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке 5. Найдите исходное число.

Самостоятельная работа “Использование систем уравнений при решении текстовых задач” (9 класс) 1 вариант

1) Найдите два натуральных числа, сумма которых равна 15, а разность равна 9.

2) В двузначном числе сумма цифр равна 12. Цифра десятков в три раза больше цифры единиц. Найдите это число.

3) Количество метров в первом куске ситца вдвое больше, чем во втором. Если от каждого из них отрезать по 13 м, то в первом куске будет в 2,5 раза больше ткани, чем во втором. Сколько метров ситца было первоначально в каждом куске?

4)Двое рабочих выполнили некоторую работу за 12 ч. Если бы сначала первый сделал половину этой работы, а затем второй- остальную её часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

5) Если двузначное число разделить на сумму его цифр, то в частном получится 7 и в остатке 6. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке число, равное сумме цифр исходного числа. Найдите исходное число.

Самостоятельная работа “Использование систем уравнений при решении текстовых задач” (9 класс) 2 вариант

1) Найдите два натуральных числа,одно из которых вдвое больше другого, а сумма этих чисел равна 18.

2) В двузначном натуральном числе сумма цифр равна 14. Цифра десятков на 4 больше цифры единиц. Найдите это число.

3) Длина гипотенузы прямоугольного треугольника равна 125 см, а сумма длин его катетов 175 см. Найдите длины катетов.

4)Двое рабочих выполнили некоторую работу за 6 ч. Если бы сначала первый сделал половину этой работы, а затем второй- остальную её часть, то вся работа была бы выполнена за 12,5 ч. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

5) Если двузначное число разделить на сумму его цифр, то в частном получится 4 и в остатке 3. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке 5. Найдите исходное число.

Самостоятельная работа “Использование систем уравнений при решении текстовых задач” (9 класс) 1 вариант

1) Найдите два натуральных числа, сумма которых равна 15, а разность равна 9.

2) В двузначном числе сумма цифр равна 12. Цифра десятков в три раза больше цифры единиц. Найдите это число.

3) Количество метров в первом куске ситца вдвое больше, чем во втором. Если от каждого из них отрезать по 13 м, то в первом куске будет в 2,5 раза больше ткани, чем во втором. Сколько метров ситца было первоначально в каждом куске?

4)Двое рабочих выполнили некоторую работу за 12 ч. Если бы сначала первый сделал половину этой работы, а затем второй- остальную её часть, то вся работа была бы выполнена за 25 ч. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

5) Если двузначное число разделить на сумму его цифр, то в частном получится 7 и в остатке 6. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке число, равное сумме цифр исходного числа. Найдите исходное число.

Самостоятельная работа “Использование систем уравнений при решении текстовых задач” (9 класс) 2 вариант

1) Найдите два натуральных числа,одно из которых вдвое больше другого, а сумма этих чисел равна 18.

2) В двузначном натуральном числе сумма цифр равна 14. Цифра десятков на 4 больше цифры единиц. Найдите это число.

3) Длина гипотенузы прямоугольного треугольника равна 125 см, а сумма длин его катетов 175 см. Найдите длины катетов.

4)Двое рабочих выполнили некоторую работу за 6 ч. Если бы сначала первый сделал половину этой работы, а затем второй- остальную её часть, то вся работа была бы выполнена за 12,5 ч. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

5) Если двузначное число разделить на сумму его цифр, то в частном получится 4 и в остатке 3. Если это же двузначное число разделить на произведение его цифр, то в частном получится 3, а в остатке 5. Найдите исходное число.

Контрольная работа “Системы уравнений с двумя переменными” (9 класс) 1 вариант

1 уровень 1) Укажите формулу расстояния между точками А(х₁,у₁) и В(х₂,у₂): а) АВ= ;

б) АВ= ;

2 уровень.2) Запишите уравнение окружности с центром в точке К(-2;3) и радиусом 4 см.

3) Найдите расстояние между точками А(10;-5) и В(3;0).

3 уровень.4)Решите систему уравнений: а) б) в)

4 уровень.5) Из пункта А в пункт В вышел пассажирский поезд, в то же время из пункта В в пункт А вышел товарный поезд. Скорость каждого на всём участке движения постоянна. Через 2 ч после того, как поезда встретились, расстояние между ними составило 280 км. Пассажирский поезд прибыл в пункт В через 9 ч, а товарный – в пункт А через 16 ч. Найдите скорость пассажирского поезда.

5 уровень.6) Решите систему уравнений:

Контрольная работа “Системы уравнений с двумя переменными” (9 класс) 2 вариант

1 уровень 1) Укажите формулу уравнения окружности с центром в точке А(х₁,у₁) и радиусом R:

а) (х-х₁)² – (у-у₁)²=R²; б) (х-х₁)² + (у-у₁)²=R²; ;

2 уровень.2) Найдите расстояние между точками А(6;4) и В(-1;-2).

3) ) Запишите уравнение окружности с центром в точке К(-1;4) и радиусом 9 см.

3 уровень.4)Решите систему уравнений: а) б) в)

4 уровень.5) Из пункта А в пункт В вышел пассажирский поезд, в то же время из пункта В в пункт А вышел товарный поезд. Скорость каждого на всём участке движения постоянна. Через 2 ч после того, как поезда встретились, расстояние между ними составило 300 км. Пассажирский поезд прибыл в пункт В через 4 ч, а товарный – в пункт А через 11 ч. Найдите скорость товарного поезда.

5 уровень.6) Решите систему уравнений:

Контрольная работа “Системы уравнений с двумя переменными” (9 класс) 1 вариант

1 уровень 1) Укажите формулу расстояния между точками А(х₁,у₁) и В(х₂,у₂): а) АВ= ;

б) АВ= ;

2 уровень.2) Запишите уравнение окружности с центром в точке К(-2;3) и радиусом 4 см.

3) Найдите расстояние между точками А(10;-5) и В(3;0).

3 уровень.4)Решите систему уравнений: а) б) в)

4 уровень.5) Из пункта А в пункт В вышел пассажирский поезд, в то же время из пункта В в пункт А вышел товарный поезд. Скорость каждого на всём участке движения постоянна. Через 2 ч после того, как поезда встретились, расстояние между ними составило 280 км. Пассажирский поезд прибыл в пункт В через 9 ч, а товарный – в пункт А через 16 ч. Найдите скорость пассажирского поезда.

5 уровень.6) Решите систему уравнений:

Контрольная работа “Системы уравнений с двумя переменными” (9 класс) 2 вариант

1 уровень 1) Укажите формулу уравнения окружности с центром в точке А(х₁,у₁) и радиусом R:

а) (х-х₁)² – (у-у₁)²=R²; б) (х-х₁)² + (у-у₁)²=R²; ;

2 уровень.2) Найдите расстояние между точками А(6;4) и В(-1;-2).

3) ) Запишите уравнение окружности с центром в точке К(-1;4) и радиусом 9 см.

3 уровень.4)Решите систему уравнений: а) б) в)

4 уровень.5) Из пункта А в пункт В вышел пассажирский поезд, в то же время из пункта В в пункт А вышел товарный поезд. Скорость каждого на всём участке движения постоянна. Через 2 ч после того, как поезда встретились, расстояние между ними составило 300 км. Пассажирский поезд прибыл в пункт В через 4 ч, а товарный – в пункт А через 11 ч. Найдите скорость товарного поезда.

5 уровень.6) Решите систему уравнений:

Контрольная работа “Системы уравнений с двумя переменными” (9 класс) 1 вариант

1 уровень 1) Укажите формулу расстояния между точками А(х₁,у₁) и В(х₂,у₂): а) АВ= ;

б) АВ= ;

2 уровень.2) Запишите уравнение окружности с центром в точке К(-2;3) и радиусом 4 см.

3) Найдите расстояние между точками А(10;-5) и В(3;0).

3 уровень.4)Решите систему уравнений: а) б) в)

4 уровень.5) Из пункта А в пункт В вышел пассажирский поезд, в то же время из пункта В в пункт А вышел товарный поезд. Скорость каждого на всём участке движения постоянна. Через 2 ч после того, как поезда встретились, расстояние между ними составило 280 км. Пассажирский поезд прибыл в пункт В через 9 ч, а товарный – в пункт А через 16 ч. Найдите скорость пассажирского поезда.

5 уровень.6) Решите систему уравнений:

С амостоятельная работа «Теорема косинусов. Решение треугольников» 1 вариант (9 класс)

1. Какое из равенств является верным: а) АС₁²=АВ²+ВС₁² – 2АВ∙ВС_1∙

б) ВС₁²=АВ²+АС₁² – 2АВ∙АС_1∙

в) АВ²=АС₁²+ВС₁² – 2АВ∙ВС_1∙

2. В треугольнике АВС: СВ=3 ; АВ=6; ∠В=45⁰. Найти АС.

3. Решите треугольник по следующим данным: а=7; в=10; с=12.

4. В параллелограмме АВСД луч ВР(Р - биссектриса тупого угла, градусная мера которого рана 120⁰. Известно, что АВ=8 см, РД=6 см. Вычислите длины диагоналей параллелограмма.

5. В равнобедренном треугольнике к боковой стороне длиной 4 см проведена медиана, равная 3 см. Найдите периметр треугольника.

С амостоятельная работа «Теорема косинусов. Решение треугольников» 2 вариант (9 класс)

1. Какое из равенств является верным: а) А₁С₁²=А₁В²+ВС₁² – 2А₁В ∙ВС_1∙

б) ВС₁²=А₁В²+А₁С₁² – 2 А₁В ∙ А₁С_1∙

в) А₁В²= А₁С₁²+ВС₁² – 2 А₁С₁∙ВС_1∙

2. В треугольнике АВС: СВ=3; АС=4; ∠С=120⁰. Найти АВ.

3. Решите треугольник по следующим данным: а=15; ∠А=36⁰; ∠В=75⁰.

4. В параллелограмме АВСД луч АТ(Т - биссектриса острого угла, градусная мера которого рана 60⁰. Известно, что АД=15 см, ВТ=10 см. Вычислите длины диагоналей параллелограмма.

5. В равнобедренном треугольнике к боковой стороне длиной 10 см проведена медиана, равная 9 см. Найдите площадь треугольника.

С амостоятельная работа «Теорема косинусов. Решение треугольников» 1 вариант (9 класс)

1. Какое из равенств является верным: а) АС₁²=АВ²+ВС₁² – 2АВ∙ВС_1∙

б) ВС₁²=АВ²+АС₁² – 2АВ∙АС_1∙

в) АВ²=АС₁²+ВС₁² – 2АВ∙ВС_1∙

2. В треугольнике АВС: СВ=3 ; АВ=6; ∠В=45⁰. Найти АС.

3. Решите треугольник по следующим данным: а=7; в=10; с=12.

4. В параллелограмме АВСД луч ВР(Р - биссектриса тупого угла, градусная мера которого рана 120⁰. Известно, что АВ=8 см, РД=6 см. Вычислите длины диагоналей параллелограмма.

5. В равнобедренном треугольнике к боковой стороне длиной 4 см проведена медиана, равная 3 см. Найдите периметр треугольника.

С амостоятельная работа «Теорема косинусов. Решение треугольников» 2 вариант (9 класс)

1. Какое из равенств является верным: а) А₁С₁²=А₁В²+ВС₁² – 2А₁В ∙ВС_1∙

б) ВС₁²=А₁В²+А₁С₁² – 2 А₁В ∙ А₁С_1∙

в) А₁В²= А₁С₁²+ВС₁² – 2 А₁С₁∙ВС_1∙

2. В треугольнике АВС: СВ=3; АС=4; ∠С=120⁰. Найти АВ.

3. Решите треугольник по следующим данным: а=15; ∠А=36⁰; ∠В=75⁰.

4. В параллелограмме АВСД луч АТ(Т - биссектриса острого угла, градусная мера которого рана 60⁰. Известно, что АД=15 см, ВТ=10 см. Вычислите длины диагоналей параллелограмма.

5. В равнобедренном треугольнике к боковой стороне длиной 10 см проведена медиана, равная 9 см. Найдите площадь треугольника.

С амостоятельная работа «Теорема косинусов. Решение треугольников» 1 вариант (9 класс)

1. Какое из равенств является верным: а) АС₁²=АВ²+ВС₁² – 2АВ∙ВС_1∙

б) ВС₁²=АВ²+АС₁² – 2АВ∙АС_1∙

в) АВ²=АС₁²+ВС₁² – 2АВ∙ВС_1∙

2. В треугольнике АВС: СВ=3 ; АВ=6; ∠В=45⁰. Найти АС.

3. Решите треугольник по следующим данным: а=7; в=10; с=12.

4. В параллелограмме АВСД луч ВР(Р - биссектриса тупого угла, градусная мера которого рана 120⁰. Известно, что АВ=8 см, РД=6 см. Вычислите длины диагоналей параллелограмма.

5. В равнобедренном треугольнике к боковой стороне длиной 4 см проведена медиана, равная 3 см. Найдите периметр треугольника.

С амостоятельная работа «Теорема косинусов. Решение треугольников» 2 вариант (9 класс)

1. Какое из равенств является верным: а) А₁С₁²=А₁В²+ВС₁² – 2А₁В ∙ВС_1∙

б) ВС₁²=А₁В²+А₁С₁² – 2 А₁В ∙ А₁С_1∙

в) А₁В²= А₁С₁²+ВС₁² – 2 А₁С₁∙ВС_1∙

2. В треугольнике АВС: СВ=3; АС=4; ∠С=120⁰. Найти АВ.

3. Решите треугольник по следующим данным: а=15; ∠А=36⁰; ∠В=75⁰.

4. В параллелограмме АВСД луч АТ(Т - биссектриса острого угла, градусная мера которого рана 60⁰. Известно, что АД=15 см, ВТ=10 см. Вычислите длины диагоналей параллелограмма.

5. В равнобедренном треугольнике к боковой стороне длиной 10 см проведена медиана, равная 9 см. Найдите площадь треугольника.

Самостоятельная работа “Арифметическая прогрессия” (9 класс) 1 вариант

1 уровень. 1) Укажите равенство для нахождения одиннадцатого члена и суммы одиннадцати первых членов арифметической прогрессии (а_п): а) а₁₁=а₁+11d; б) S₁₁= в) S₁₁= ; г) а₁₁=а₁+10d.

2 уровень. 2) Какие из последовательностей являются арифметической прогрессией:

а) -4;-1;2;5;8;…; б)0;3;8;13;18;23…?

3) В арифметической прогрессии (а_n) известно, что а₁=-5,2 и d=6. Найдите а₈.

3 уровень. 4) Для данной арифметической прогрессии: 17;24;31;… укажите значение разности d и формулу n-го члена а_n; найдите S₅.

4 уровень.5)Найдите сумму пятнадцати первых членов арифметической прогрессии, если её третий член -6, а шестой равен 1,2.

.5 уровень. 6) Найдите сумму всех натуральных чисел кратных 6 и меньших 200.

Самостоятельная работа “Арифметическая прогрессия” (9 класс) 2 вариант

1 уровень. 1) Укажите равенство для нахождения девятого члена и суммы девяти первых членов арифметической прогрессии (а_п): а) а₉=а₁+9d; б) S₉= в) S₉= ; г) а₉=а₁+8d.

2 уровень. 2) Какие из последовательностей являются арифметической прогрессией:

а) -5;-7;-9;-11;-13…; б)0;3;6;9;13;…?

3) В арифметической прогрессии (а_n) известно, что а₁=2,7 и d=-3. Найдите а₉.

3 уровень. 4) Для данной арифметической прогрессии: 18;23;28;… укажите значение разности d и формулу n-го члена а_n; найдите S₄.

4 уровень.5)Найдите сумму десяти первых членов арифметической прогрессии, если её четвёртый член равен -7, а седьмой равен 1,4.

.5 уровень. 6) Найдите сумму всех натуральных чисел кратных 8 и меньших 250.

Самостоятельная работа “Арифметическая прогрессия” (9 класс) 1 вариант

1 уровень. 1) Укажите равенство для нахождения одиннадцатого члена и суммы одиннадцати первых членов арифметической прогрессии (а_п): а) а₁₁=а₁+11d; б) S₁₁= в) S₁₁= ; г) а₁₁=а₁+10d.

2 уровень. 2) Какие из последовательностей являются арифметической прогрессией:

а) -4;-1;2;5;8;…; б)0;3;8;13;18;23…?

3) В арифметической прогрессии (а_n) известно, что а₁=-5,2 и d=6. Найдите а₈.

3 уровень. 4) Для данной арифметической прогрессии: 17;24;31;… укажите значение разности d и формулу n-го члена а_n; найдите S₅.

4 уровень.5)Найдите сумму пятнадцати первых членов арифметической прогрессии, если её третий член -6, а шестой равен 1,2.

.5 уровень. 6) Найдите сумму всех натуральных чисел кратных 6 и меньших 200.

Самостоятельная работа “Арифметическая прогрессия” (9 класс) 2 вариант

1 уровень. 1) Укажите равенство для нахождения девятого члена и суммы девяти первых членов арифметической прогрессии (а_п): а) а₉=а₁+9d; б) S₉= в) S₉= ; г) а₉=а₁+8d.

2 уровень. 2) Какие из последовательностей являются арифметической прогрессией:

а) -5;-7;-9;-11;-13…; б)0;3;6;9;13;…?

3) В арифметической прогрессии (а_n) известно, что а₁=2,7 и d=-3. Найдите а₉.

3 уровень. 4) Для данной арифметической прогрессии: 18;23;28;… укажите значение разности d и формулу n-го члена а_n; найдите S₄.

4 уровень.5)Найдите сумму десяти первых членов арифметической прогрессии, если её четвёртый член равен -7, а седьмой равен 1,4.

.5 уровень. 6) Найдите сумму всех натуральных чисел кратных 8 и меньших 250.

Самостоятельная работа “Арифметическая прогрессия” (9 класс) 1 вариант

1 уровень. 1) Укажите равенство для нахождения одиннадцатого члена и суммы одиннадцати первых членов арифметической прогрессии (а_п): а) а₁₁=а₁+11d; б) S₁₁= в) S₁₁= ; г) а₁₁=а₁+10d.

2 уровень. 2) Какие из последовательностей являются арифметической прогрессией:

а) -4;-1;2;5;8;…; б)0;3;8;13;18;23…?

3) В арифметической прогрессии (а_n) известно, что а₁=-5,2 и d=6. Найдите а₈.

3 уровень. 4) Для данной арифметической прогрессии: 17;24;31;… укажите значение разности d и формулу n-го члена а_n; найдите S₅.

4 уровень.5)Найдите сумму пятнадцати первых членов арифметической прогрессии, если её третий член -6, а шестой равен 1,2.

.5 уровень. 6) Найдите сумму всех натуральных чисел кратных 6 и меньших 200

Самостоятельная работа “Правильные многоугольники” (9 класс) 1 вариант

1 уровень.1) Выберите верное утверждение: центром окружности, вписанной в треугольник, служит точка пересечения его: а) медиан; б)высот; в)биссектрис; г)серединных перпендикуляров к сторонам треугольника.

2 уровень:2) а) Найдите градусную меру угла правильного пятиугольника;

б) Чему равен радиус окружности, вписанной в правильный треугольник со стороной 2 см.

3 уровень:3) Дан куб АВСDА₁В₁С₁D₁. Окружность, длина радиуса которой равна 2 см, касается всех сторон грани А₁В₁С₁D₁ в их серединах. Вычислите площадь полной поверхности куба.

4 уровень:4) Длина стороны правильного треугольника , вписанного в окружность, равна 4 см. Вычислите площадь квадрата, вписанного в эту же окружность.

5 уровень:5) Диагонали BT и CP правильного шестиугольника ABCDTP пересекаются в точке О. Площадь четырёхугольника АBCO равна 18 см². Вычислите расстояние между центрами окружностей, вписанных в BCO и

Самостоятельная работа “Правильные многоугольники” (9 класс) 2 вариант

1 уровень.1) Выберите верное утверждение: центром окружности, описанной около треугольника, служит точка пересечения его: а) медиан; б)высот; в)биссектрис; г)серединных перпендикуляров к сторонам треугольника.

2 уровень:2) а) Найдите градусную меру угла правильного восьмиугольника;

б) Чему равен радиус окружности, описанной около правильного треугольник со стороной см.

3 уровень:3) Дана прямая треугольная призма, у которой АА₁ =АВ. Окружность касается всех сторон треугольника А₁В₁С₁ в их серединах. Вычислите длину радиуса окружности, если площадь боковой поверхности

призмы равна 27 см².

4 уровень:4)Около квадрата, длина стороны которого равна 4 см, описана окружность, а около окружности – правильный шестиугольник. Найдите площадь шестиугольника.

5 уровень:5) Диагонали CP и АД правильного шестиугольника ABCDTP пересекаются в точке О. Площадь четырёхугольника СДТР равна 27 см². Вычислите периметр треугольника, вершинами которого являются центры окружностей, вписанных в треугольники ОCД, ОТД и Д

Самостоятельная работа “Правильные многоугольники” (9 класс) 1 вариант

1 уровень.1) Выберите верное утверждение: центром окружности, вписанной в треугольник, служит точка пересечения его: а) медиан; б)высот; в)биссектрис; г)серединных перпендикуляров к сторонам треугольника.

2 уровень:2) а) Найдите градусную меру угла правильного пятиугольника;

б) Чему равен радиус окружности, вписанной в правильный треугольник со стороной 2 см.

3 уровень:3) Дан куб АВСDА₁В₁С₁D₁. Окружность, длина радиуса которой равна 2 см, касается всех сторон грани А₁В₁С₁D₁ в их серединах. Вычислите площадь полной поверхности куба.

4 уровень:4) Длина стороны правильного треугольника , вписанного в окружность, равна 4 см. Вычислите площадь квадрата, вписанного в эту же окружность.

5 уровень:5) Диагонали BT и CP правильного шестиугольника ABCDTP пересекаются в точке О. Площадь четырёхугольника АBCO равна 18 см². Вычислите расстояние между центрами окружностей, вписанных в BCO и

Самостоятельная работа “Правильные многоугольники” (9 класс) 2 вариант

1 уровень.1) Выберите верное утверждение: центром окружности, описанной около треугольника, служит точка пересечения его: а) медиан; б)высот; в)биссектрис; г)серединных перпендикуляров к сторонам треугольника.

2 уровень:2) а) Найдите градусную меру угла правильного восьмиугольника;

б) Чему равен радиус окружности, описанной около правильного треугольник со стороной см.

3 уровень:3) Дана прямая треугольная призма, у которой АА₁ =АВ. Окружность касается всех сторон треугольника А₁В₁С₁ в их серединах. Вычислите длину радиуса окружности, если площадь боковой поверхности

призмы равна 27 см².

4 уровень:4)Около квадрата, длина стороны которого равна 4 см, описана окружность, а около окружности – правильный шестиугольник. Найдите площадь шестиугольника.

5 уровень:5) Диагонали CP и АД правильного шестиугольника ABCDTP пересекаются в точке О. Площадь четырёхугольника СДТР равна 27 см². Вычислите периметр треугольника, вершинами которого являются центры окружностей, вписанных в треугольники ОCД, ОТД и Д

Самостоятельная работа “Геометрическая прогрессия” (9 класс) 1 вариант

1 уровень. 1) Укажите равенства для нахождения четвёртого члена и суммы первых четырёх членов геометрической прогрессии (в_п): а) в₄=в₁∙q³; б) S₄= в) S₄= ; г) в₄=в₁∙q⁴.

2 уровень. 2) Какие из последовательностей являются геометрической прогрессией:

а) -4;-2;-1; ; ;…; б)1;3;9;18;27;36…?

3) В геометрической прогрессии (в_n) известно, что в₁=3 и q=2. Найдите в₉.

3 уровень. 4) Для данной геометрической прогрессии: 9;3;1; … укажите значение знаменателя q и формулу n-го члена в_n; найдите S₅.

4 уровень.5)Найдите сумму пяти первых членов геометрической прогрессии, если в₂=21, в₄=189, q .

6) Решите уравнение:1+х+х²+…+х²⁰⁰=0.

.5 уровень. 6) Найдите первый член геометрической прогрессии, которая состоит из шести членов: если сумма трёх её членов с нечётными номерами равна 273, а сумма трёх остальных членов равна 91.

Самостоятельная работа “Геометрическая прогрессия” (9 класс) 2 вариант

1 уровень. 1) Укажите равенства для нахождения седьмого члена и суммы первых семи членов геометрической прогрессии (в_п): а) в₇=в₁∙q⁷; б) S₇= в) S₇=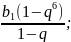 ; г) в₇=в₁∙q⁶.

2 уровень. 2) Какие из последовательностей являются геометрической прогрессией:

а) -5;1;5;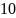 ; …; б)2;-1; ; …?

3) В геометрической прогрессии (в_n) известно, что в₁=12 и q=-2. Найдите в₅.

3 уровень. 4) Для данной геометрической прогрессии: 16;8;4; … укажите значение знаменателя q и формулу n-го члена в_n; найдите S₄.

4 уровень.5)Найдите сумму пяти первых членов геометрической прогрессии, если в₂=4, в₄=36, q .

6) Решите уравнение:1-у+у²-у³+…+у¹⁵⁰=0.

.5 уровень. 7) Найдите первый член геометрической прогрессии, которая состоит из шести членов: если сумма первых трёх её членов равна 56, а сумма трёх последних членов равна 7.

Самостоятельная работа “Геометрическая прогрессия” (9 класс) 1 вариант

1 уровень. 1) Укажите равенства для нахождения четвёртого члена и суммы первых четырёх членов геометрической прогрессии (в_п): а) в₄=в₁∙q³; б) S₄= в) S₄= ; г) в₄=в₁∙q⁴.

2 уровень. 2) Какие из последовательностей являются геометрической прогрессией:

а) -4;-2;-1; ; ;…; б)1;3;9;18;27;36…?

3) В геометрической прогрессии (в_n) известно, что в₁=3 и q=2. Найдите в₉.

3 уровень. 4) Для данной геометрической прогрессии: 9;3;1; … укажите значение знаменателя q и формулу n-го члена в_n; найдите S₅.

4 уровень.5)Найдите сумму пяти первых членов геометрической прогрессии, если в₂=21, в₄=189, q .

6) Решите уравнение:1+х+х²+…+х²⁰⁰=0.

.5 уровень. 6) Найдите первый член геометрической прогрессии, которая состоит из шести членов: если сумма трёх её членов с нечётными номерами равна 273, а сумма трёх остальных членов равна 91.

Самостоятельная работа “Геометрическая прогрессия” (9 класс) 2 вариант

1 уровень. 1) Укажите равенства для нахождения седьмого члена и суммы первых семи членов геометрической прогрессии (в_п): а) в₇=в₁∙q⁷; б) S₇= в) S₇= ; г) в₇=в₁∙q⁶.

2 уровень. 2) Какие из последовательностей являются геометрической прогрессией:

а) -5;1;5; ; …; б)2;-1; ; …?

3) В геометрической прогрессии (в_n) известно, что в₁=12 и q=-2. Найдите в₅.

3 уровень. 4) Для данной геометрической прогрессии: 16;8;4; … укажите значение знаменателя q и формулу n-го члена в_n; найдите S₄.

4 уровень.5)Найдите сумму пяти первых членов геометрической прогрессии, если в₂=4, в₄=36, q .

6) Решите уравнение:1-у+у²-у³+…+у¹⁵⁰=0.

.5 уровень. 7) Найдите первый член геометрической прогрессии, которая состоит из шести членов: если сумма первых трёх её членов равна 56, а сумма трёх последних членов равна 7.

Контрольная работа «Правильные многоугольники. Длина окружности и площадь круга»(9 класс) 1 вариант

1 уровень. 1) Выберите и запишите формулу, которая выражает а) площадь круга: 1)S=πR²; 2) S=2πR; 3) S=7πR²;

б) длину дуги окружности с градусной мерой : 1) 𝓁=

2 уровень. 2)Найдите площадь круга, ограниченного окружностью, длина которой равна 60 см.

3 уровень.3)Две точки окружности делят её на две дуги, градусные меры которых относятся как 10:8. Найдите длины этих дуг, если радиус окружности равен 6 см.

4 уровень.4)Длина стороны правильного треугольника, вписанного в окружность, равна 4 см. Вычислите площадь квадрата, вписанного в ту же окружность.

5 уровень. 5)Диагонали ромба ABCD пересекаются в точке O. На отрезке АО как на диаметре построен круг. Окружность, ограничивающая круг, пересекает сторону AD в точке P. Известно, что AP = 6 см, а PD = 2 см. Вычислите площадь части круга, расположенной вне ромба.

Контрольная работа «Правильные многоугольники. Длина окружности и площадь круга»(9 класс) 2 вариант

1 уровень. 1) Выберите и запишите формулу, которая выражает а) длину окружности: 1)С=4πR²; 2) С=2πR;

3) С=πR²; б) площадь кругового сектора, ограниченного дугой с градусной мерой : 1) S=

2 уровень. 2)Найдите длину окружности, ограничивающей круг, площадь которой равна 225 см².

3 уровень. 3)Две точки окружности делят её на две дуги, разность градусных мер которых равна 50 . Найдите длины этих дуг, если радиус окружности равен 10 см.

4 уровень. 4)Около квадрата, длина стороны которого равна 4 см, описана окружность, а около окружности – правильный шестиугольник. Найдите площадь шестиугольника.

5 уровень. 5)Диагонали ромба ABCD пересекаются в точке O. На отрезке CO как на диаметре построен круг. Окружность, ограничивающая круг, пересекает сторону BC в точке T. Известно, что TB = см, а точка O удалена от стороны ромба на расстояние, равно 3 см. Вычислите площадь части круга, расположенной вне ромба.

Контрольная работа «Правильные многоугольники. Длина окружности и площадь круга»(9 класс) 1 вариант

1 уровень. 1) Выберите и запишите формулу, которая выражает а) площадь круга: 1)S=πR²; 2) S=2πR; 3) S=7πR²;

б) длину дуги окружности с градусной мерой : 1) 𝓁=

2 уровень. 2)Найдите площадь круга, ограниченного окружностью, длина которой равна 60 см.

3 уровень.3)Две точки окружности делят её на две дуги, градусные меры которых относятся как 10:8. Найдите длины этих дуг, если радиус окружности равен 6 см.

4 уровень.4)Длина стороны правильного треугольника, вписанного в окружность, равна 4 см. Вычислите площадь квадрата, вписанного в ту же окружность.

5 уровень. 5)Диагонали ромба ABCD пересекаются в точке O. На отрезке АО как на диаметре построен круг. Окружность, ограничивающая круг, пересекает сторону AD в точке P. Известно, что AP = 6 см, а PD = 2 см. Вычислите площадь части круга, расположенной вне ромба.

Контрольная работа «Правильные многоугольники. Длина окружности и площадь круга»(9 класс) 2 вариант

1 уровень. 1) Выберите и запишите формулу, которая выражает а) длину окружности: 1)С=4πR²; 2) С=2πR;

3) С=πR²; б) площадь кругового сектора, ограниченного дугой с градусной мерой : 1) S=

2 уровень. 2)Найдите длину окружности, ограничивающей круг, площадь которой равна 225 см².

3 уровень. 3)Две точки окружности делят её на две дуги, разность градусных мер которых равна 50 . Найдите длины этих дуг, если радиус окружности равен 10 см.

4 уровень. 4)Около квадрата, длина стороны которого равна 4 см, описана окружность, а около окружности – правильный шестиугольник. Найдите площадь шестиугольника.

5 уровень. 5)Диагонали ромба ABCD пересекаются в точке O. На отрезке CO как на диаметре построен круг. Окружность, ограничивающая круг, пересекает сторону BC в точке T. Известно, что TB = см, а точка O удалена от стороны ромба на расстояние, равно 3 см. Вычислите площадь части круга, расположенной вне ромба.

Контрольная работа №1 “Центральные и вписанные углы. Замечательные точки треугольника » (9 кл) 1 вариант

1 уровень. 1) АВ и АС – касательные к окружности,

В и С – точки касания. Верно ли, что АС = 14,6 ?

2 уровень.2)Используя данные рисунка, найдите градусную меру угла α. О- центр окружности.

3 уровень.3)Через точку А окружности с центром О проведены касательная АМ и хорда АВ, ∠АОВ = 80⁰. Чему равен угол МАВ?

4 уровень.4) Вершины треугольника АВС лежат на окружности так, что сторона АС является её диаметром. Серединный перпендикуляр к стороне ВС пересекает сторону АС в точке О. Вычислите радиус окружности, если известно, что АВ= 6 см, а ∠ВОС = 120⁰.

5 уровень. 5) Вершины треугольника АВС лежат на окружности, диаметром которой является отрезок СВ. Прямая 𝓁 касается окружности в точке А и пересекает луч СВ в точке Т. Известно, что ТВ:ТС= 1:2, АТ= 3 см. Вычислите площадь треугольника АВТ.

Контрольная работа №1 “Центральные и вписанные углы. Замечательные точки треугольника » (9 кл) 2 вариант

1 уровень. 1) MN и MK– касательные к окружности,

N и K – точки касания. Верно ли, что MN = 5,4 ?

2 уровень.2)Используя данные рисунка, найдите градусную меру угла α. Точка О- центр окружности.

3 уровень.3)Через точку M окружности с центром О проведены касательная МN и хорда МК, ∠NMK = 58⁰. Чему равен угол МОК?

4 уровень.4) Вершины треугольника АВС лежат на окружности так, что сторона АВ является её диаметром. Серединный перпендикуляр к стороне АС пересекает сторону АВ в точке О. Вычислите радиус окружности, если известно, что отношение градусных мер меньших дуг СВ и АС равно и Р_СВО=18 см..

5 уровень. 5) Вершины треугольника АВС лежат на окружности, диаметром которой является отрезок СВ. Прямая 𝓁 касается окружности в точке А и пересекает луч СВ в точке О. Известно, что АО:ОВ= 2:1, а радиус окружности равен 3 см. Вычислите отношение площадей треугольников АОВ и АОС.

Вариант 1

Решите неравенства: а) 2х²-3х-5 б) 4х² 36; в) –х²-2х +8

Вариант 2

Решите неравенства: а) 5х²+3х-2 б) 2х² 32; в) –х²+7х -12

Вариант 3

Решите неравенства: а) х²+5х+6 б) 2х² 50; в) х²- 8х +12

Вариант 4

Решите неравенства: а) 2х²-3х-2 б) 3х² 12; в) 2х²+5х -7

Вариант 1

Решите неравенства: а) 2х²-3х-5 б) 4х² 36; в) –х²-2х +8

Вариант 2

Решите неравенства: а) 5х²+3х-2 б) 2х² 32; в) –х²+7х -12

Вариант 3

Решите неравенства: а) х²+5х+6 б) 2х² 50; в) х²- 8х +12

Вариант 4

Решите неравенства: а) 2х²-3х-2 б) 3х² 12; в) 2х²+5х -7

Вариант 1

Решите неравенства: а) 2х²-3х-5 б) 4х² 36; в) –х²-2х +8

Вариант 2

Решите неравенства: а) 5х²+3х-2 б) 2х² 32; в) –х²+7х -12

Вариант 3

Решите неравенства: а) х²+5х+6 б) 2х² 50; в) х²- 8х +12

Вариант 4

Решите неравенства: а) 2х²-3х-2 б) 3х² 12; в) 2х²+5х -7

Вариант 1

Решите неравенства: а) 2х²-3х-5 б) 4х² 36; в) –х²-2х +8

Вариант 2

Решите неравенства: а) 5х²+3х-2 б) 2х² 32; в) –х²+7х -12

Вариант 3

Решите неравенства: а) х²+5х+6 б) 2х² 50; в) х²- 8х +12

Вариант 4

Решите неравенства: а) 2х²-3х-2 б) 3х² 12; в) 2х²+5х -7

Вариант 1

Решите неравенства: а) 2х²-3х-5 б) 4х² 36; в) –х²-2х +8

Вариант 2

Решите неравенства: а) 5х²+3х-2 б) 2х² 32; в) –х²+7х -12

Вариант 3

Решите неравенства: а) х²+5х+6 б) 2х² 50; в) х²- 8х +12

Вариант 4

Решите неравенства: а) 2х²-3х-2 б) 3х² 12; в) 2х²+5х -7

Вариант 1

Решите неравенства: а) 2х²-3х-5 б) 4х² 36; в) –х²-2х +8

Вариант 2

Решите неравенства: а) 5х²+3х-2 б) 2х² 32; в) –х²+7х -12

Вариант 3

Решите неравенства: а) х²+5х+6 б) 2х² 50; в) х²- 8х +12

Вариант 4

Решите неравенства: а) 2х²-3х-2 б) 3х² 12; в) 2х²+5х -7

Проверочная работа «Метод интервалов» ( 9 класс) 1 вариант

Решите неравенства:

1. (х+6)(х-8) 2) (2,5х-5)(1,6х-2) 3) (7х-14)(3х-15)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 2 вариант

Решите неравенства:

1. (х+4)(х-12) 2) (2х-12)(11+33х) 3) (12х-3)(2х-3)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 1 вариант

Решите неравенства:

1. (х+6)(х-8) 2) (2,5х-5)(1,6х-2) 3) (7х-14)(3х-15)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 2 вариант

Решите неравенства:

1. (х+4)(х-12) 2) (2х-12)(11+33х) 3) (12х-3)(2х-3)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 1 вариант

Решите неравенства:

1. (х+6)(х-8) 2) (2,5х-5)(1,6х-2) 3) (7х-14)(3х-15)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 2 вариант

Решите неравенства:

1. (х+4)(х-12) 2) (2х-12)(11+33х) 3) (12х-3)(2х-3)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 1 вариант

Решите неравенства:

1. (х+6)(х-8) 2) (2,5х-5)(1,6х-2) 3) (7х-14)(3х-15)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 2 вариант

Решите неравенства:

1. (х+4)(х-12) 2) (2х-12)(11+33х) 3) (12х-3)(2х-3)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 1 вариант

Решите неравенства:

1. (х+6)(х-8) 2) (2,5х-5)(1,6х-2) 3) (7х-14)(3х-15)х(8-х) 4)

Проверочная работа «Метод интервалов» ( 9 класс) 2 вариант

Решите неравенства:

1. (х+4)(х-12) 2) (2х-12)(11+33х) 3) (12х-3)(2х-3)х(8-х) 4)