- •Табличный метод
- •5) Основные этапы проектирования электромеханического привода
- •7) Характеристика заклёпочных соединений. Расчёт заклёпочных швов
- •8) Конструкции и расчёт на прочность сварных соединений
- •Метод расчета: основные параметры
- •9) Соединения деталей склеиванием и пайкой. Области применения и расчёт Соединение пайкой и склеиванием
- •10) Прессовые соединения (соединения с натягом). Области применения и расчёт.
- •11) Основные типы и геометрические параметры резьбы
- •12) Расчёт резьбы на прочность
- •13) Расчёт стержня болта (винта) на прочность, при различных способах нагружения
- •14) Характеристика шпоночных соединений. Расчёт шпонок на прочность
- •Шпоночное соединение: вал, ступица, призматическая шпонка
- •Шпоночное соединение призматической шпонкой
- •Призматические шпонки
- •Виды шпонок: призматическая, сегментная, клиновая
- •15) Шлицевые соединения. Расчёт на смятие
- •6.5. Пример расчета шпоночного у. Шалевого соединений
- •16) Характеристика клеммовых соединений. Расчёт на прочность
- •17) Основные типы ременных передач. Основы расчёта. Достоинства и недостатки. Ременные передачи
- •14.1. Общие сведения
- •14.2. Классификация передач
- •14.3. Достоинства и недостатки ременных передач трением
- •14.4. Конструкция и материалы ремней
- •14.5. Основные геометрические соотношения
- •14.6. Взаимодействие ремня со шкивами, критерии расчета ременных передач.
- •14.7. Кинематика ременных передач
- •14.8. Силы и напряжения в ремне
- •14.9. Расчет ременной передачи по тяговой способности, кпд передачи
- •14.10. Расчет долговечности ремня
- •18) Конструкции и основные характеристики цепных передач. Достоинства и недостатки. Цепные передачи
- •13.1. Общие сведения
- •13.2. Достоинства и недостатки цепных передач
- •13.3 Типы цепей
- •13.4. Критерии работоспособности цепных передач
- •13.5 Материалы и термическая обработка деталей цепей
- •13.6 Основные параметры цепных передач
- •19) Общие сведения о геометрии и кинематики зубчатых передач. Их достоинства и недостатки.
- •18) Конструкции и основные характеристики цепных передач. Достоинства и недостатки.
14.7. Кинематика ременных передач
Окружные скорости ( м/с ) на шкивах (рис. 14.1):
 и
и  ,
( 14.8 )
,
( 14.8 )
где d1 и d2 – диаметры ведущего и ведомого шкивов, мм; n1 и n2 – частоты вращения шкивов, мин-1.
Окружная скорость на ведомом шкиве v2 меньше скорости на ведущем v1 вследствие скольжения:
![]() .
( 14.9 )
.
( 14.9 )
Передаточное отношение:
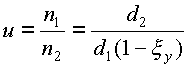 .
( 14.10 )
.
( 14.10 )
Обычно упругое скольжение находится в пределах 0,01…0,02 и растет с увеличением нагрузки.
14.8. Силы и напряжения в ремне
Окружная сила на шкивах (Н):
![]()
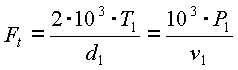 ,
( 14.11 )
,
( 14.11 )
где T1 – вращающий момент, Н м, на ведущем шкиве диаметром d1, мм; P1 – мощность на ведущем шкиве, кВт.
С другой стороны, Ft = F1 - F2, где F1 и F2 - силы натяжения ведущей и ведомой ветвей ремня под нагрузкой. Сумма натяжений ветвей при передаче полезной нагрузки не меняется по сравнению с начальной: F1 + F2 = 2F0. Решая систему двух уравнений, получаем:
F1 = F0 + Ft/2, F2 = F0 – Ft/2. ( 14.12 )
Сила
начального натяжения ремня F0 должна
обеспечивать передачу полезной нагрузки
за счет сил трения между ремнем и шкивом.
При этом натяжение должно сохраняться
долгое время при удовлетворительной
долговечности ремня. С ростом силы ![]() несущая
способность ременной передачи возрастает,
однако срок службы уменьшается.
несущая
способность ременной передачи возрастает,
однако срок службы уменьшается.
Соотношение
сил натяжения ведущей и ведомой ветвей
ремня без учета центробежных сил
определяют по уравнению Эйлера,
выведенному им для нерастяжимой нити,
скользящей по цилиндру. Записываем
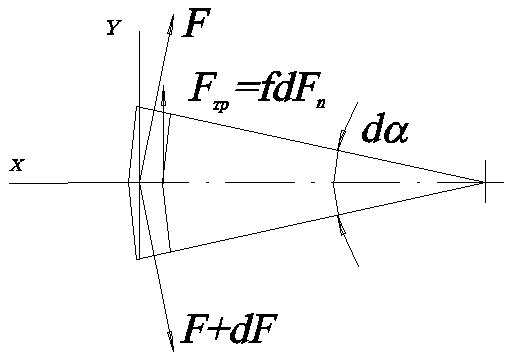
условия равновесия по осям x и y элемента
ремня с центральным углом d (рис.
14.6). Принимаем, что 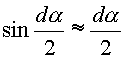 и
и 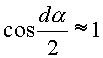 ,
тогда,
,
тогда,
![]()
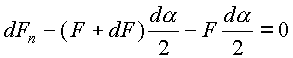 (
14.13 )
(
14.13 )
![]()
![]() ,
( 14.14 )
,
( 14.14 )
|
Рис. 14.6 |
где dFn – нормальная сила реакции, действующая на элемент ремня от шкива; f –коэффициент трения ремня по шкиву. Из ( 14.13 ) имеем:
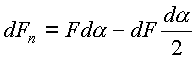 .
Подставим значение
.
Подставим значение ![]() в
( 14.14 ), пренебрегая членом
в
( 14.14 ), пренебрегая членом 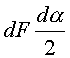 в
связи с его малостью. Тогда
в
связи с его малостью. Тогда ![]() и
и
 (
14.15 )
(
14.15 )
Интегрируем по дуге скольжения, подставляя пределы F1, F2, 0,
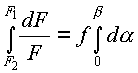 ,
, ![]() .
.
После
потенцирования имеем:  ,
( 14.16 )
,
( 14.16 )
где e –
основание натурального логарифма, -
угол, на котором происходит упругое
скольжение, при номинальной нагрузке ![]() .
.
Полученная
зависимость показывает, что
отношение F1/F2 сильно
зависит от коэффициента трения ремня
на шкиве и угла ![]() .
Но эти величины являются случайными, в
условиях эксплуатации могут принимать
весьма различные значения из числа
возможных, поэтому силы натяжения ветвей
в особых случаях уточняют экспериментально.
.
Но эти величины являются случайными, в
условиях эксплуатации могут принимать
весьма различные значения из числа
возможных, поэтому силы натяжения ветвей
в особых случаях уточняют экспериментально.
Обозначая ![]() и
учитывая, что
и
учитывая, что ![]() ,
имеем
,
имеем
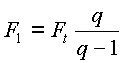 и
и  .
( 14.17 )
.
( 14.17 )
Ремни обычно неоднородны по сечению. Условно их рассчитывают по номинальным (средним) напряжениям, относя силы ко всей площади поперечного сечения ремня и принимая справедливым закон Гука.
Нормальное напряжение от окружной силы Ft:
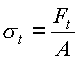 ,
( 14.18 )
,
( 14.18 )
где A – площадь сечения ремня, мм2.
Нормальное напряжение от предварительного натяжения ремня
 .
( 14.19 )
.
( 14.19 )
Нормальные напряжения в ведущей и ведомой ветвях:
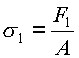 и
и 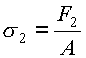 .
( 14.20 )
.
( 14.20 )
Центробежная сила вызывает нормальные напряжения в ремне, как во вращающемся кольце:
![]() ,
( 14.21 )
,
( 14.21 )
где ц –
нормальные напряжения от центробежной
силы в ремне, МПа; v1 –
скорость ремня, м/с; ![]() -
плотность материала ремня, кг/м3.
-
плотность материала ремня, кг/м3.
При
изгибе ремня на шкиве диаметром d относительное
удлинение наружных волокон ремня как
изогнутого бруса равно 2y/d,
где y –
расстояние от нейтральной линии в
нормальном сечении ремня до наиболее
удаленных от него растянутых волокон.
Обычно толщина ремня ![]() .
Наибольшие напряжения изгиба возникают
на малом шкиве и равны:
.
Наибольшие напряжения изгиба возникают
на малом шкиве и равны:
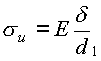 .
( 14.22 )
.
( 14.22 )
Максимальные суммарные напряжения возникают на дуге сцепления ремня с малым (ведущим) шкивом:
![]() .
( 14.23 )
.
( 14.23 )
|
Рис. 14.7 |
Эти напряжения (рис. 14.7) используют в расчетах ремня на долговечность, так как при работе передачи в ремне возникают значительные циклические напряжения изгиба и в меньшей мере циклические напряжения растяжения из-за разности натяжения ведущей и ведомой ветвей ремня.