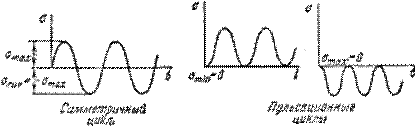15. Гипотеза потенциальной энергии формоизменения. Теория прочности Мора.

Четвертая (энергетическая) гипотеза прочности: количество удельной потенциальной энергии изменения формы, накопленной к моменту наступления предельного состояния материала, одинаково как при сложном напряженном состоянии, так и при простом одноосном растяжении.

В четвертой гипотезе прочности речь идет не обо всей удельной потенциальной энергии деформации, а лишь ее части, которая накапливается за счет изменения формы кубика с ребром равным единице. В общем случае полная удельная потенциальная энергия деформации может быть представлена как сумма энергий, связанных с изменением объема кубика и изменением его формы. Условие прочности по четвертой гипотезе прочности: Достоинство четвертой гипотезы прочности: эквивалентное напряжение определяется значениями всех трех главных напряжений.

Согласно гипотезе прочности Мора, предложенной Отто Мором, два напряженных состояния равноопасны, если для соответствующих главных напряжений  и  соблюдается соотношение:  . Условие прочности по гипотезе прочности Мора:  Гипотеза прочности Мора не учитывает влияния второго главного напряжения ( ). Коэффициент  представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, который равен для хрупких материалов:  , для пластичных:  .

16. Изгиб с кручением балок круглого и прямоугольного сечения.

При изгибе с кручением в поперечных сечениях стержня возникают изгибающие моменты Мх, Мy, крутящий момент Мк и в некоторых случаях поперечные силы Qx, Qy. Поперечными силами будем пренебрегать. .    или    . Осевой момент сопротивления для круга  ,

17. Сложные виды нагружения сопромат

Растяжение (сжатие) возникает в случае, когда стержень нагружен силами, совпадающими по направлению с его осью. Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого, при неизменном расстоянии между ними. Кручение возникает при действии на стержень внешних сил, образующих моменты относительно продольной оси стержня. Изгиб - это такой вид нагружения, когда внешние силы вызывают моменты относительно оси симметрии (или главной оси), расположенной в плоскости поперечного сечения. Этот момент называется изгибающим. (Косой изгиб, Внецентренное растяжение – сжатие

18. Косой изгиб.

Косой изгиб проявляется, если прикладываем к балке вертикальную нагрузку, и она при этом изгибается не только в вертикальной плоскости, но и вбок. Косой изгиб - это изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости. Косой изгиб возникнет, если силовая плоскость не будет совпадать ни с одной из главных плоскостей балки. Если изготовить балку с нарушением технологии, то влияние косого изгиба будет проявляться в увеличении нормальных напряжений, приводящего к снижению способности балки переносить нагрузки. Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).

19. Внецентренное растяжение – сжатие.

Вторым практически важным случаем сложения деформаций от изгиба и от продольных сил является так называемое внецентренное сжатие или растяжение, вызываемое одними продольными силами. Этот вид деформации получается при действии на стержень двух равных и прямопротивоположных сил Р, направленных по прямой АА, параллельной оси стержня

20. Изгиб бруса большой кривизны

Брус, продольная ось симметрии, которого кривая линия – кривой брус. При изгибе возникает нормальная сила, и изгибающий момент. Наиболее нагруженные точки находятся на внутренней цилиндрической поверхности. σ = N/A+Myi/Aei(r-yi) где N – нормальная сила, A – площадь сечения, M – изгибающий момент, yi – радиус от нейтральной линии до рассматриваемого волокна, ei – экстрентриситет (расстояние от нейтральной осью и осью, проходящей через центр тяжести поперечного сечения), r – радиус кривизны бруса. При изгибе бруса напляжения распределяются нелинейно по высоте бруса. Гиперболическая зависимость закона распределения нормальных напряжений по высоте поперечного сечения следуетт из формулы выше.

21. Формула Лапласа. Расчет тонкостенных сосудов

Оболочка – тело одно из измерений которого (толщина) значительно меньше 2ух других.σm/pm+σt/pt=p/h – ф-ла Лапласа σ – напряжения,( t – окружное напряжение, m – меридианное напряжение(направлен по дуге мередианы) рм – радиус кривизныдуги меридиана срединной поверхности, pt – второй главный радиус, т.е. радиус кривизны нормального сечения. H – толщина.

22. Циклическое нагружение. Характеристики цикла.

Циклические нагрузки испытывают многие элементы конструкций: валы и оси, детали механизмов и т.п. Циклические нагрузки характеризуются следующими параметрами:Т – период изменения нагрузки, число циклов действия данной переменной нагрузки,N- число циклов действия данной переменной нагрузки до разрушения, smax– наибольшие напряжение цикла, smin- наименьшее напряжение цикла, - коэффициент асимметрии цикла, - амплитуда цикла, - среднее напряжение. В случае, когда  и цикл называется симметричным. Такой цикл, в частности, имеет место в рассмотренном выше примере вращающейся оси вагона). Если   или же  , цикл называется пульсационным. Для пульсационного цикла r = 0 или  . Циклы, имеющие одинаковые показатели r, называются подобным