1.Стержневая система, Классификация стержневых систем.

  Под стержневой системой понимается всякая конструкция, состоящая из элементов, имеющих форму бруса. Если элементы конструкции работают только на растяжение или сжатие система называется фермой (рис.6.1). Ферма состоит из шарнирно опертых между собой прямых стержней, образующих треугольники и для нее характерно приложение внешних сил в узлах заданной системы.

 Если элементы стержней системы работают в основном на изгиб или кручение, то такая система называется рамой (рис.6.2).

Если все элементы стержневой системы расположены в одной плоскости, в которой также действуют все внешние силы, включая реакции опор, то система называется плоской (рис.6.1, 6.2).

 Если все элементы заданной системы расположены в одной плоскости, а внешние силы действуют в перпендикулярной плоскости, то система называется плоскопространственной (рис.6.3). Стержневые системы, не относящиеся к двум указанным категориям, называются пространственными (рис.6.4).

 Все стержневые системы принято разделять на статически определимые и статически неопределимые. Под статически определимой понимается такая система, для которой усилия во всех ее элементах могут быть определены по методу сечений с применением лишь уравнений равновесия. Если этого сделать нельзя, то такая система называется статически неопределимой.

2.Теорема о взаимности работ и перемещений

∆12Р1=∆21Р2 работа силы   (или первой группы сил) на перемещениях, вызванных силой   (второй группой сил), равна работе силы   на перемещениях, вызванных силой  . δ12=δ21перемещение точки приложения первой единичной силы по ее направлению, вызванное действием второй единичной силы, равно перемещению точки приложения второй единичной силы по ее направлению, вызванному действием первой единичной силы.

Теорема о взаимности работ гласит, что работа первой силы на перемещении точки ее приложения под действием второй силы равна работе второй силы на перемещении точки ее приложения под действием первой силы, т.е. F₁ у₁₂ = F₂ у₂₁ = W

Если силы равны, то теорема переходит в теорему о взаимности перемещений: перемещение первого сечения под действием силы, приложенной во втором сечении, равно перемещению второго сечения под действием той же силы, но приложенной в первом сечении. у₁₂ = у₂₁.

3. Теорема Кастилиано.

Теорема Кастилиано: частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по направлению этой силы. .

U - потенциальная энергия, Р – сила

Перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии деформации по этой силе  .

Для определения перемещения (линейного или углового) в точке, где по условию задачи внешнее усилие (сила или момент) отсутствует, необходимо приложить в этом месте фиктивную обобщенную силу. Далее следует написать выражение для потенциальной энергии деформации от всех сил, включая и фиктивную, и взять от этого выражения производную по фиктивной силе. В полученном выражении для обобщенного перемещения фиктивную нагрузку необходимо принять равной нулю.

4. Интегралы Мора для определения перемещений в стержневых системах.

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. .

5. Понятие о степенях свободы и связи. Метод сил. Канонические уравнения метода сил.

Под числом степеней свободы следует понимать число независимых координат, определяющих положение точки или тела в пространстве или на плоскости. Свободная точка на плоскости имеет две степени свободы – координаты х и у Устройство, уничтожающее степень свободы, называется связью. В зависимости от соотношения между числом степеней свободы и числом связей, накладываемых на тело, различают еще несколько классификаций стержневых систем. В соответствии с этой классификацией существуют три типа стержневых систем: геометрически изменяемые, геометрически неизменяемые и мгновенно изменяемые системы. метод сил заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. 

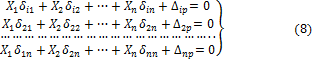
6. Расчет статически неопределимых балок и рам. Использование свойств симметрии.

Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции.

7. Определение перемещений в статически неопределимых системах.

Таким образом, чтобы найти перемещение в С.Н.С. нужно:

1. Раскрыть статическую неопределимость и построить окончательную эпюру.

2. К основной системе приложить единичную силу и построить эпюру.

3. Перемножить две эти эпюры.

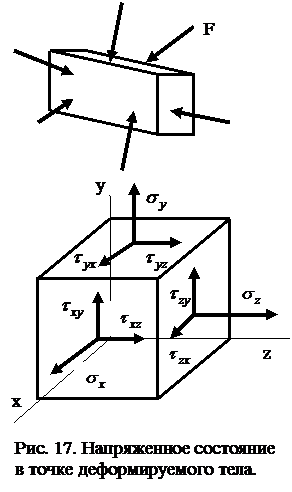
8. Наряженное состояние в точке. Тензоры напряжений и деформаций.

Напряженное состояние в точке – совокупность напряжений, действующих во множестве площадок, проходящих через данную точку. Те́нзор деформа́ции — тензор, который характеризует сжатие (растяжение) и изменение формы в каждой точке тела при деформации.

9. Определение напряжений в наклонных площадках.

На наклонной площадке полные напряжения будут направлены вдоль продольной оси и распределены равномерно. Оставшаяся часть стержня находится в равновесии. Поэтому равнодействующие внешней нагрузки   и полных напряжений  должны быть равны между собой, т.е.

где   площадь наклонного сечения. Полное напряжение   на наклонной площадке составит

10. Главные площадки и главные напряжения

Главные площадки – это площадки, проходящие через исследуемую точку, на которых Касательные напряжения отсутствуют. Главные напряжения – это возникающие на главных площадках нормальные напряжения

В общем случае нагружения (при объемном напряженном состоянии) среди множества площадок, проходящих через некоторую точку тела, всегда можно найти три взаимно перпендикулярные главные площадки.  Главные напряжения обозначаются  .

11. Исследование напряженного состояния с помощью круга Мора.