Тема: Кинетика Задачи

Задача 1. Водород находится в сосуде при температуре 300 К и давлении 2 атм.. Принимая во внимание распределение Больцмана по скоростям, вывести формулу для давления газа и вычислить число столкновений в 1 с, испытываемых участком стенки сосуда площадью 10 . Чему равно среднее время между двумя столкновениями?

Решение. Будем предполагать, что между не имеющими размеров молекулами идеально газа не происходит столкновений. В то же время учтем распределение скоростей по абсолютной величине и по направлениям. Рассмотрим на стенке сосуда площадку размером и определим число попадающих на эту площадку за время dt частиц, имеющих скорость от v до v + dv,

и угол падения от до . Эти частицы заключены в цилиндре, объем которого равен

(1)

(рис.2). Из числа содержащихся в частиц под углом к стенке, лежащем в пределах от до , движутся

(2)

частиц, имеющих произвольный азимутальный угол . (Фактически при фиксированном угле молекулы летят из пространства между двумя конусами.- Ред.). Величину С определим из условия

или (3)

откуда

. (4)

Если теперь учесть распределение скоростей Максвелла – Больцмана, то для числа dv частиц, сталкивающихся с площадкой и имеющих при этом скорость и угол падения, заключенных в интервалах от v до v + dv, и от до , согласно (1) и (4) получаем

, (5)

где f(v) – функция распределения.

При каждом соударении стенке передается импульс

. (6)

Отсюда находим силу, действующую на площадку :

. (7)

Полную силу, приложенную к площадке , получим посредством интегрирования по всем углам падения и по всем скоростям v. В результате после деления на находим давление

(8)

Интегрирование по углу в (8) дает

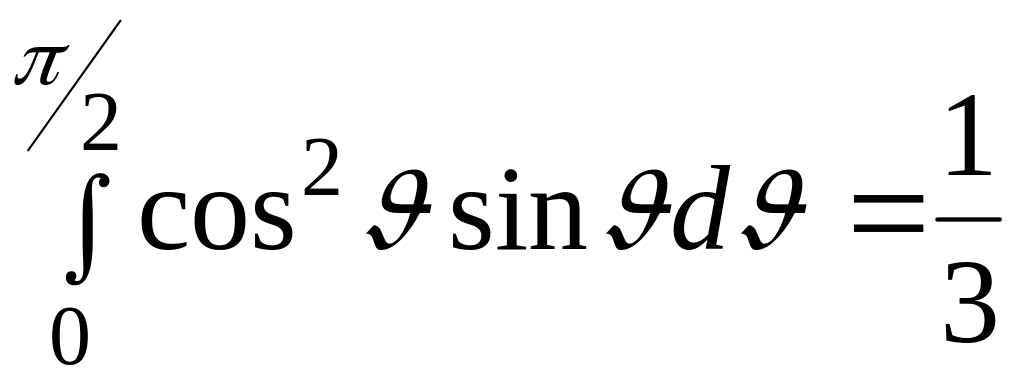, (9)

а интегрируя по скоростям, получаем

. (10)

Таким образом, статистическая модель, учитывающая больцмановское распределение по скоростям, приводит к следующему выражению для давления:

. (11)

Подставляя сюда вместо числа частиц в выражение и используя соотношение , получаем

. (12)

Для вычисления среднего числа столкновений необходимо проинтегрировать выражение (5). Тогда для числа столкновений, происходящих за 1 с, имеем

. (13)

Необходимые нам интегралы имеют следующие значения:

, (14)

. (15)

Таким образом, для числа столкновений в единицу времени имеем

, (16)

где относительная молекулярная масса, число кило-молей в объеме V. Используя уравнение состояния идеального газа, можно записать выражение (16) для числа столкновений в в виде

. (17)

Подставляя численные значения, найдем число столкновений с участком площадью :

.

Отсюда определяем среднее время между двумя столкновениями с площадкой :

.

Задача 2. Вычислить число столкновений молекул водорода при температуре и давления 0,5 атм. Чему равна средняя длина свободного пробега ? Найти полное число столкновений в 1 кмоле водорода. Молекулы рассматривать как невзаимодействующие твердые шары, движущиеся с одинаковыми скоростями. Газокинетический эффективный диаметр принять равным .

Решение. Рассмотрим две частицы, которые движутся со скоростями и . Если , то их относительная скорость составляет

, (1)

где угол между векторами этих скоростей. Усреднение по всем направлениям дает

. (2)

С данной молекулой за 1 с в среднем столкнуться все молекулы, центры тяжести которых окажутся внутри кругового цилиндра с основанием и высотой . Если в содержится , то число столкновений для одной частицы составляет

. (3)

В качестве величины v используем среднее значение для распределения Максвелла – Больцмана

. (4)

Величину найдем из уравнения состояния для . Тогда формула (3) дает для числа столкновений

. (5)

В рассматриваемой модели средняя длина свободного пробега есть

. (6)

В 1 кмоль содержится молекул. Полное число столкновений, происходящих в 1 кмоле за 1 с, составляет

. (7)

Подставив численные выражения, получим ,

.

Задача 3. Смесь из 3 л водорода и 1 л азота находится при нормальных условиях. Найти число столкновений между молекулами в 1 с. Чему равны средние длины пробега между соударениями различных частиц?(Диаметр газокинетического эффективного сечения составляет: ,

, относительные молекулярные массы: , .).

Решение. Число столкновений частиц сорта 1 с частицами сорта 2 составляет

. (1)

Аналогично получим число столкновений частиц 2 с частицами 1

. (2)

Полное число соударений частиц 1 и 2 в объеме , есть

. (3)

В данном случае полный объем газа . Для парциальных давлений имеем , , а плотность числа частиц , ( ).

Число столкновений между частицами двух в объеме V = 4л равно

; (4)

При заданных числовых значениях имеем

Средняя длина свободного пробега частицы 1 между соударениями с частицами 2 составляет

. (5)

Подставив численные значения, получим длину свободного пробега молекул водорода между столкновениями с молекулами азота:

.

Для средней длины свободного пробега молекул азота между столкновениями с молекулами водорода имеем

.

Задача 4. В тонкостенном сосуде, помещенном в вакуум, имеется очень маленькое отверстие, на которое извне направляется параллельный пучок одноатомных молекул, летящих с одной и той же скоростью , перпендикулярно к площади отверстия. Концентрация молекул в пучке равна . Найти в установившемся равновесном состоянии среднюю скорость , концентрацию молекул и температуру газа в сосуде.

Решение. Из-за столкновений молекул со стенками сосуда и между собой внутри сосуда устанавливается максвелловское распределение скоростей. Условие сохранения числа частиц и кинетической энергии газа в сосуде имеют вид

, .

Используя их, а также формулу , находим

, , .

Задача 5. Найти полную кинетическую энергию молекул идеального одноатомного газа, ударяющихся о квадратный сантиметр стенки в единицу времени.

Ответ: Для максвелловского распределения .

Задача 6. В тонкостенном сосуде, содержащем идеальный одноатомный газ при температуре , имеется очень маленькое отверстие, через которое молекулы вылетают в вакуум. Определить среднее значение кинетической энергии вылетевшей молекулы в предположении, что за время опыта изменения числа молекул и температуры газа в сосуде пренебрежимо малы.

Ответ: .

Задача 7. Определить, какая часть молекул идеального газа, столкнувшихся со стенкой сосуда за определенное время (например, за одну секунду), имеет кинетическую энергию, превосходящую .

Ответ: .

Задача 8. В опыте Штерна на поверхности вращающегося цилиндра С конденсируются молекулы серебра с различными скоростями. Каким скоростям молекул, попадающих на пластинку DF, соответствует ее наибольшее почернение?

Решение.

F

C

D

Если установка неподвижна, то молекулы конденсируются в точке D. При вращении всей установки молекулы со скоростями попадают в F. Смещение по дуге DF равно , где постоянная прибора. Число молекул со скоростями между и , ежесекундно испускаемых источником A, пропорционально . Выражая через , подставим его в виде . Отсюда видно, что линейная плотность распределения молекул, сконденсировавшихся по поверхности цилиндра, пропорциональна , т.е. . Эта плотность максимальна при , где наиболее вероятная скорость.

Задача 9. Газ состоит из молекул с массами и , концентрации которых равны соответственно и . Найти выражение для средней длины свободного пробега молекулы каждого газа с учетом максвелловского распределения скоростей.

Ответ: ,

.

Задача 10. Для приближенного вычисления средней длинны свободного пробега молекулы, Клаузиус предположил, что все молекулы газа движутся с одинаковыми скоростями, направления которых распределены в пространстве изотропно. Получить выражение для в этом предположении.

Р ешение.

Найдем среднюю скорость молекул относительно одной из них (например, правой). Относительная скорость молекулы, движущейся под углом к скорости первой молекулы , определяется выражением

.

Число молекул, скорости которых образуют с направлением углы между и , дается формулой

.

Используя ее, получаем

.

После этого по формуле

находим

.

Задача 11. Найти выражение для среднего полного числа столкновений молекул газа в единице объема газа в единицу времени.

Решение. Число столкновений одной молекулы с остальными дается выражением

.

Для молекул его надо умножить на и разделить на два. Деление на два необходимо потому, что при нашем подсчете каждая молекула учитывается дважды: один раз как ударяющая, другой – как ударяемая. В результате получаем

.

Задача 12. Газ состоит из смеси двух газов с концентрациями и . Найти выражение для среднего полного числа столкновений молекул одного газа с молекулами другого газа в единице объема в единицу времени.

Ответ: .

Задача 13. Показать, что в системе центра масс рассеяние шаров при упругих столкновениях сферически симметрично.

Решение. Пусть скорость скорость первого, а скорость второго шара ( см.рис.). В системе центра масс

.

При столкновении шары в этой системе обмениваются нормальными компонентами импульсов, тогда, как касательные компоненты их остаются неизменными. Отсюда следует, что скорости шаров в системе центра масс не изменяются по величине, а только поворачиваются на один и тот же угол (угол рассеяния). Пусть угол, который образовали в момент удара начальные скорости шаров с линией центров. Тогда, как видно из рисунка , т.е. . Прицельное расстояние .

Пусть , а площадь кольца с радиусами и .Тогда . Вероятность рассеяния в телесный угол равна , т.е. пропорциональна . Коэффициент пропорциональности не зависит от , а это значит, что расстояние сферически симметрично.

Задача 14. Оценить порядок величины максимальной скорости, с которой артиллерийский снаряд может вылететь из ствола орудия. Какие требования нужно предъявить патрону, чтобы эта скорость была, как можно большей?

Решение. Когда снаряд движется в стволе орудия со скоростью, превышающей скорость теплового движения молекул пороховых газов, последние почти перестают оказывать давление на дно снаряда и ускорять его. Отсюда следует, что максимально достижимая скорость снаряда, при вылете из ствола орудия, будет порядка средней скорости теплового движения молекул пороховых газов. Она тем больше, чем больше температура пороховых газов и чем меньше их молекулярная масса. [6]