1.Охарактеризуйте зонную схему кристаллических тел, полупроводников, проводников, диэлектриков. Хуй

2.Получите зависимость концентрации свободных носителей в полупроводнике от положения уровня Ферми.

В отличие от металлов, в которых электронных газ является вырожденным и подчиняется статистике Ферми-Дирана, в собственных и слаболегированных примесных полупроводниках электронный (дырочный) газ является невырожденным и распределение электронов по состояниям описывается классической статистикой Максвелла-Больцмана. Для таких полупроводников концентрация свободных носителей зависит от положения уровня Ферми и температуры Т. При температуре отличной от нуля в зоне проводимости полупроводника находятся электроны и в валентной зоне дырки. Обозначим их концентрацию через n и р.

Определим равновесную концентрацию электронов проводимости в зоне проводимости. При этом за нулевой уровень отсчета энергии электронов принимается потолок валентной зоны.

Концентрацию электронов , энергия которых заключена в интервале от Е до E+dE можно выразить следующим образомdn=Nn(E)*2f_M-БdE, (2.2.1)

где Nn(E) - число элементарных фазовых ячеек или состояний, приходящихся на единичный интервал энергии;f_M-Б- функция распределения Максвелл-Больцмана,

f_M-Б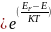 , выражающая вероятность заполнения электроном с энергией Е фазовой ячейки.

Множитель 2 выражает принцип Паули.Как нам известно

Тогда (2.2.1) можно записать в виде . (2.2.2)

Полное число электронов n , находящихся при температуре Т в зоне проводимости, можно получить интегрируя (2.2.2) по всем значениям энергии соответствующим зоне проводимости .(2.2.3)

Проинтегрировав (2.2.3) получим .(2.2.4)

Если провести подобный расчет для дырок, то можно получить аналогичное выражение .(2.2.5)

В (2.2.4) и (2.2.5) m_n и m_p эффективные массы дырок и электронов.

Из выражений (2.2.4) и (2.2.5) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми E_F, чем больше это расстояние, тем ниже концентрация носителей.

Произведение n на р для любого невырожденного полупроводника равно: .(2.2.6)

Это формула показывает, что при фиксированной температуре произведение концентраций электронов и дырок для данного полупроводника является величиной постоянной. Соотношение (2.2.6) выражает так называемый закон действующих масс в применении к газу свободных носителей в полупроводниках.

3.Охарактеризуйте положение уровня Ферми и концентрацию носителей в собственных полупроводниках.

Если в полупроводнике нет примесей, так что N_A=N_D=0, где N_A и N_D - концентрации соответственно акцепторной и донорной примесей, то такой полупроводник называется собственным или чистым. В собственных полупроводниках концентрация электронов в зоне проводимости n_i равна концентрации дырок в валентной зоне p_i._i=p(2.3.1) Индексами «i» обозначают равновесные концентрации в собственных полупроводниках. Приравнивая правые части соотношений (2.2.4) и (2.2.5) получаем

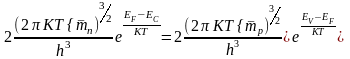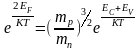, ,откуда 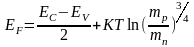. (2.3.2)

Это соотношение определяет положение уровня Ферми в собственных полупроводниках. При абсолютном нуле Т=0: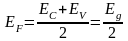 ,(2.3.3)

где Eg - ширина запрещенной зоны. Т.е. при Т=0 уровень Ферми располагается посередине запрещенной зоны.

С повышением температуры он смещается вверх к дну зоны проводимости, если m_p>m_n и вниз если m_p<m_n (рис. 2.4). Однако, в большинстве случаев это смещение настолько незначительно, что им можно пренебречь и считать, что уровень Ферми в собственных полупроводниках располагается по середине зоны.

Если подставить E_F из (2.3.3) в (2.2.4) и (2.2.5), то получим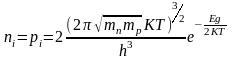 . (2.3.4)

Из (2.3.4) следует, что равновесная концентрация носителей заряда в собственном полупроводнике определяется шириной запрещенной зоны E_g. При чем зависимость n_i от T и E_g очень сильная.

Из (2.3.4) можно получить: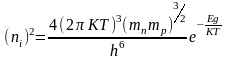 . (2.3.5)

Правые части (2.3.5) и (2.2.6) равны , следовательно, равны и левые

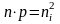. (2.3.6)

Это выражение также выражает закон действующих масс. Из (2.3.6) следует, что концентрация электронов и дырок в любом невырожденном полупроводнике таковы, что их произведение равно квадрату собственной концентрации электронов. Соотношение (2.3.6) справедливо при любой температуре

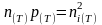. (2.3.7)