29. Предмет (цель) вариационного исчисления.

Вариации: http://www.studfiles.ru/preview/3299944/

https://ru.wikipedia.org/wiki/%D0%92%D0%B0%D1%80%D0%B8%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%BE%D0%B5_%D0%B8%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5

Вариационное исчисление изучает вариации функционалов, к примеру, нахождение функции, на которой данный функционал достигает экстремального значения (экстремали).

1. нахождение точек в пространстве функций, на котором определён функционал — точек стационарного функционала, стационарных функций, линий, траекторий, поверхностей и т. п., то есть нахождение для заданного {\displaystyle \Phi [f]}  таких {\displaystyle f} , для которых {\displaystyle \delta \Phi =0}  при любом (бесконечно малом) {\displaystyle \delta f} , или, иначе, где {\displaystyle {\frac {\delta \Phi }{\delta f}}=0} ,

2. нахождение локальных экстремумов функционала, то есть в первую очередь определение тех {\displaystyle f} , на которых {\displaystyle \Phi [f]}  принимает локально экстремальные значения — нахождение экстремалей (иногда также определение знака экстремума).

Классическое вариационное исчисление посвящено анализу условий экстремума интегрального функционала

На некотором множестве G функцийx(t), определенных и дифференцируемых на некотором множестве Ω СRⁿ, со значениями на множестве R. Множество G определяется обычно дополнительными оговорками или условиями; множество Ω как правило связно и имеет связную внутренность.

Задачей оптимального управления является предсказание управления в виде функции времени. Такая функция, воздействующая на объект, должна «заставить его работать» на интервале управления таким образом, чтобы критерий качества достигал своего возможно наименьшего значения. Для выбора этой оптимальной управляющей функции из всех возможных функций необходимо знать состояние объекта в начале интервала.

С точки зрения математики задача оптимального управления представ-ляет собой задачу минимизации функционала, рассматриваемую в вариационном исчислении. Она сходна с обычной задачей минимизации в математическом анализе, когда необходимые условия, которым должны удовлетворять независимые переменные скалярной функции, определяются приравниванием нулю всех частных производных функций по своим аргументам. При минимизации функционала получается не система алгебраических уравнений, которым удовлетворяют независимые перемен-ные в точке минимума скалярной функции, а система дифференциальных уравнений, которым на интервале управления удовлетворяют управления и состояния (экстремали), являющиеся функциями времени и соответ-ствующие экстремуму критерия качества. Кроме того, процедура минимиза-ции функционала усложняется из-за необходимости удовлетворять ограничениям, налагаемым на переменные управлений и состояний. Эти ограничения связаны с динамикой объекта и задаются уравнениями состояний. Ограничения в виде уравнений состояний можно учесть в задаче минимизации функционала, используя метод множителей Лагранжа.

В данном случае вводится мера ошибки, учитывающая ограничения. Пусть уравнения состояний имеют вид

x(t) = a [x(t), u(t), t]

при начальных условиях x (t₀) = x₀.

Задача заключается в нахождении необходимых условий, которым должны удовлетворять переменные x(t) и u(t) (t₀ ≤ t ≤ t₁ ) в точке экстремума критерия качества при условии, что уравнения состояний налагают ограничения на функции x(t) и u(t).

Воспользуемся идеей множителей Лагранжа и введем меру ошибки при ограничениях

F_c [x(t), (t), u(t), λ(t), t]=F[x(t), u(t), t]+λ^T(t){a[x(t), u(t), t] – (t)} ,(7.8)

где λ – n-мерный вектор множителей Лагранжа. В формуле (7.8) предполага-ется, что функции x(t), (t), u(t) и λ(t) независимы.

Определяя соответствующий критерий качества при ограничениях

η_с = 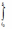F_c (x, , u, λ, t) dt,

воспользуемся вариационными принципами минимизации функционалов для отыскания необходимых условий, которым должны удовлетворять экстремали x*(t),u*(t) и λ*(t). Такой анализ приводит к необходимым условиям, записываемым в виде:

уравнений управлений

= 0; (7.9)

уравнений состояний

= 0; (7.10)

уравнений Эйлера – Лагранжа (сопряженных)

– = 0; (7.11)

условий трансверсальности

[ ^T, ] . (7.12)

Необходимые условия (7.9) – (7.12) имеют фундаментальное значение в оптимальном управлении, так как они составляют основу для определения оптимальных траекторий.

ПРИМЕР: ????