2.1 Первый алгоритм Гомори

Рассмотрим полностью целочисленную задачу линейного программирования, в которой n₁ = n.

Пусть  – оптимальный опорный план задачи  на целочисленность. Если они все целые, то . Если хотя бы одна координата, допустим , будет нецелой, поступим следующим образом.

Обозначим через N совокупность небазисных переменных и на основании последней симплексной таблицы выразим целевую функцию и все переменные  через небазисные переменные :

(20)

Так как  – нецелая величина, обозначим ближайшее целое число, не превосходящее , через 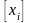(целая часть ) и определим дробную часть числа

(21)

Очевидно, .

Теорема 1: Пусть – допустимое решение задачи . Тогда соотношение

(22)

определяют правильное отсечение.

Доказательство: Запишем выражение (21) в виде

Используя выражение (22), получим

Или

.

На основании предположения теоремы о допустимости решения задачи  и – целые. Величины  и целые по определению. Следовательно,  тоже целое.

Докажем, что . Предположим, что . Это значит, что

По определению дробной части . По условию теоремы x – допустимое решение задачи , поэтому . Следовательно, , . Отсюда , или, что то же самое, . Итак,  – нецелое, а это противоречит только что доказанному. Следовательно, предположение  неверное.

Теорема доказана.

Следствие: Любое оптимальное решение задачи , не являющиеся допустимым решением задачи  не удовлетворяет условию правильного отсечения (22).

Доказательство: Пусть – оптимальное решение задачи , –дробное. Покажем, что  не удовлетворяет условию отсечения. Из оптимальности плана  следует, что . Поэтому . Учитывая это, подставим  в выражение (22):

что противоречит условию .

Важной проблемой метода отсечения является нарастание количества дополнительных ограничений по мере решения вспомогательных задач, оптимальные планы которых будут содержать нецелые координаты, т.е. возникает проблема размерности. Гомори предложил прием, ограничивающий размеры рассматриваемых расширенных симплексных таблиц числом , где n – количество переменных задач , k – число ее небазисных переменных. Этот прием основан на том, что дополнительные ограничения (правильные отсечения)  интересуют нас лишь как способ отсечения нецелочисленного оптимального решения  и перехода от задачи  к задаче . Заметим, что переменная  выводится из базиса сразу же после введения ограничения:

,

.

[5]

2.2 Второй алгоритм Гомори

Данный алгоритм предназначен для решения задач, в которых требование целочисленности наложено на некоторые переменные (в частности и на все). Рассмотрим его применение к частично целочисленным задачам линейного программирования, имея в виду, что вычислительная схема будет справедлива и для полностью целочисленных задач. Пусть требуется максимизировать функцию

(23)

при условиях

(24)

(25)

(26)

Метод решения задачи (23) – (26) основывается на той же идее, что и метод решения полностью целочисленных задач. Сформулируем второй алгоритм Гомори в виде следующей теоремы.

Теорема 2: Пусть  – оптимальное решение задачи  и  – соответствующая симплексная таблица. Если – не целое, то неравенство

(27)

или, что то же самое,

(28)

(29)

где

(30)

(31)

определяет оптимальное отсечение.

Мы проверим лишь условие отсечения. Для этого докажем, что оптимальное решение задачи , не являющееся допустимым решением исходной задачи (23) – (26), не удовлетворяет условиям отсечения. Пусть в оптимальном решении  величина  нецелая, . Так как в оптимальном решении все небазисные переменные равны нулю:

( )

Тогда формула (8) примет вид

Поскольку по условию теоремы . Условие отсечения выполнено.

Правило построения правильного отсечения: Пусть  не удовлетворяет условию целочисленности (26) и  – симплекс-таблица, соответствующая полученному оптимальному решению задачи . Выберем

и построим правильное отсечение по формулам (28) – (31).

[11]