МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДИРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«СЕВЕРО-КАВКАЗСКАЯ ГОСУДАРСТВЕННАЯ ГУМАНИТАРНО-ТЕХНИЧЕСКАЯ АКАДЕМИЯ»

Кафедра «Математика»

КУРСОВАЯ РАБОТА

по дисциплине «Методы оптимизации»

Тема: «Решение задач целочисленного программирования»

Выполнил:

студент 2 курса

Кармов И.А.

Руководитель:

Байрамукова З.Х.

Черкесск 2016

Содержание

Введение

1.Теоретический аспект целочисленного программирования………………….4

1.1 Предпосылки появления целочисленного программирования……………..4

1.2 Основные понятия целочисленного программирования……………………4 1.3 Целочисленное программирование как метод оптимизации……………….4

2. Методы решения задач целочисленного программирования………………...7

2.1 Симплекс-метод……………………………………………………………….7

2.2 Первый алгоритм Гомори……………………………………………………14

2.3 Второй алгоритм Гомори…………………………………………………….16

2.4 Метод ветвей и границ……………………………………………………….18

Решение задачи ЛП в неканонической форме симплекс-методом……………21

Заключение……………………………………………………………………….23

Список литературы………………………………………………………………24

Введение

При рассмотрении целого ряда задач финансового менеджмента и бизнеса необходимо учитывать требование целочисленности используемых переменных. Такие задачи называются задачами целочисленного программирования.

Под задачей целочисленного программирования понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования. Особый интерес к задачам целочисленного програмирования вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных.

Цель работы: Рассмотреть методы решения задач целочисленного линейного программирования.

1.Теоретический аспект целочисленного программирования

1.1 Предпосылки появления целочисленного программирования

Целочисленное программирование возникло в 50-60-е годы нашего века из нужд практики - главным образом в работах американских математиков Дж.Данцига и Р.Гомори. Первоначально целочисленное программирование развивалось независимо от геометрии чисел на основе теории и методов математической оптимизации, прежде всего линейного программирования. Однако в последние время исследования в этом направлении все чаще проводятся средствами математики целых чисел.

Задачи такого типа весьма актуальны, так как к их решению сводится анализ разнообразных ситуаций, возникающих в экономике, технике, военном деле и других областях. С появлением ЭВМ, ростом их производительности повысился интерес к задачам такого типа и к математике в целом.

[12]

1.2 Основные понятия целочисленного программирования

Целочисленным (иногда его называют также дискретным) программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные накладывается условие целочисленности, а область допустимых решений конечна. Огромное количество экономических задач носит дискретный, чаще всего целочисленный характер, что связано, как правило, с физической неделимостью многих элементов расчета: например, нельзя построить два с половиной завода, купить полтора автомобиля и т.д. В ряде случаев такие задачи решаются обычными методами, например, симплексным методом, с последующим округлением до целых чисел. Однако такой подход оправдан, когда отдельная единица составляет очень малую часть всего объема (например, товарных запасов); в противном случае он может внести значительные искажения в действительно оптимальное решение. Поэтому разработаны специальные методы решения целочисленных задач.

[6]

1.3 Целочисленное программирование как метод оптимизации

Оптимальность - выбор наилучшего варианта из множества допустимых или имеющихся в наличии вариантов. Суть принципа оптимальности состоит в выборе такого планового управленческого решения, где его компоненты расположены в наилучшем порядке и учитывают внутренние возможности и внешние условия.

Принцип оптимальности в практике планирования и управления – это решение экстремальной задачи вида . Функция, указанная в данном определении является целевой функцией. Целевая функция позволяет выбирать наилучший вариант из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение. Для реализации условия оптимальности необходимы указания системы ограничений

(1)

Задача оптимизации в общем случае, включает три компоненты - целевую функцию F, ограничения g_i и граничные условия, и имеет следующую математическую постановку:

(2)

где a_j и b_j —нижнее и верхнее предельно допустимые значения х_j.

Задачу (2) можно представить в еще более общей компактной форме записи

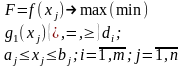(3)

Граничные условия показывают предельно допустимые значения искомых переменных, и в общем случае они могут быть двусторонними типа

Задачи оптимального программирования классифицируются:

1. по характеру изменения переменных:

- линейные;

- нелинейные.

2. по характеру изменения переменных:

- непрерывные;

- дискретные.

3. по учету фактора времени:

- статические;

- динамические.

4. по наличию информации о переменных:

- полная определенность;

- в условиях неполной информации;

- задачи в условиях неопределенности.

5. по числу критериев оценки альтернативы:

-однокритериальные;

- многокритериальные.

Частный раздел оптимального программирования являющийся в свою очередь разделом прикладной математики изучающий задачи условной оптимизации является - линейное программирование.

Задача линейного программирования, для которой используются возможные способы решения, должна быть записана в канонической форме.

Целевая функция имеет вид:

(4)

Ограничения имеют вид

(5)

Вектор удовлетворяющий системе ограничений называется допустимым решением (планом задачи линейного программирования). План, который доставляет максимум или минимум целевой функции называется оптимальным планом задачи линейного программирования.

Наиболее распространенным методом решения линейного программирования является симплекс-метод.

И так, целочисленным программированием называется раздел математического программирования, изучающий экстремальные задачи, в которых решение задач оптимизации должны быть целые числа, тогда такие задачи называются задачами целочисленного программирования, но в том случае если ограничения и целевая функция задачи представляют собой линейные зависимости.

[1]