
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •8) Площадь круга равна . Найдите длину его окружности.
- •Задание 8
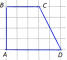
- •7) Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. Рис.). Ответ дайте в квадратных сантиметрах.
- •Задание 9
- •Задание 10
- •Задание 11
- •Задание 12
Задание 6
1)

2)

3)

4)

5) Поставьте в соответствие каждому неравенству множество его решений.

6)

7)

8)

9)

10)

Задание 7
1) В треугольнике АВС известно, что АВ = ВС = 17, АС = 16. Найдите длину медианы ВМ.

2) Стороны параллелограмма равны 45 и 54. Высота, проведенная к большей стороне, равна 20. Найдите высоту, проведенную к меньшей стороне параллелограмма.

3) В треугольнике АВС угол С прямой, АС = 6, ВС = 8. Найдите радиус вписанной окружности.

4) В треугольнике АВС известно, что АВ = ВС = 13, медиана ВМ = 12. Найдите длину АС. (см. рис. к задаче 1)
5) В треугольнике АВС АС = ВС = 16, cos А = 0,75. Найдите АВ.
6) Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

7) Площадь круга
равна
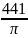 .
Найдите длину его окружности.
.
Найдите длину его окружности.
8) Площадь круга равна . Найдите длину его окружности.
9) Две стороны
параллелограмма относятся
как
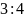 ,
а периметр его равен 70. Найдите
большую сторону параллелограмма.
,
а периметр его равен 70. Найдите
большую сторону параллелограмма.

10) . В треугольнике АВС угол С равен 58°, AD и BE – биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Задание 8
1) Палисад имеет форму прямоугольника, стороны которого равны 2,5 м и 7 м. Длинной стороной палисад примыкает к дому. Найдите длину забора (в метрах), которым необходимо огородить оставшуюся часть палисада.
2) Участок земли под застройку имеет форму прямоугольника со сторонами 35 и 50 м. Определите длину ограждения (в метрах), которым будет обнесён по периметру этот участок, если в ограждении нужно предусмотреть ворота шириной 4 м.
3) Квартира общей площадью 57 кв. м. включает в себя гостиную 4 м х 5 м, спальню 3 м х 5 м и кухню 4 м х 3 м. Оставшуюся площадь занимают подсобные помещения. Определите площадь подсобных помещений.
4) План земельного участка разбит на клетки. Каждая клетка обозначает квадрат со стороной 10 м. Найдите площадь земельного участка (в кв. м).
5) Два дачника, имеющие одинаковые прямоугольные участки 20 м х 30 м с общей границей, договорились вырыть общий прямоугольный пруд 10 м х 14 м таким образом, чтобы он занимал одинаковую площадь на каждом из двух участков. Какова площадь (в кв. м) оставшейся части каждого из участков?

6) Найдите площадь
четырехугольника,
изображенного на клетчатой
бумаге с размером клетки
1 см ![]() 1
см (см. рис.). Ответ дайте в квадратных
сантиметрах.
1
см (см. рис.). Ответ дайте в квадратных
сантиметрах.

7) Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. Рис.). Ответ дайте в квадратных сантиметрах.

8) Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

9) Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.

10) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

11) Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.

12) Найдите среднюю линию трапеции ABCD, если стороны квадратных клеток равны 1.

13) Точки O(0; 0), A(10; 0), B(8; 6), C(2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.

14) Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
15)
Найдите сторону квадрата,
диагональ которого равна 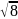 .
.
