14. Структурные средние: мода и медиана, их сущность и порядок расчёта в дискретных и интервальных рядах.
В качестве структурных средних чаще всего используют показатели моды и медианы. Мода (Мо) – наиболее часто повторяющееся значение признака. Медиана (Ме) – величина признака, которая делит упорядоченный ряд на две равные по численности части.Если расчет моды и медианы проводится в дискретном ряду, то он опирается на их понятия. В интервальном ряду распределения для расчета моды и медианы применяют следующие формулы.Мода рассчитывается по формуле
,где
хМо
– нижнее значение модального интервала;
iМо
– размер модального интервала; fМо–
частота модального интервала; fМо–1
– частота, предшествующая модальной
частоте; fМо+1
– частота, последующая за модальной
частотой.Модальному интервалу
соответствует наибольшая (модальная)
частота. Медиана рассчитывается по
формуле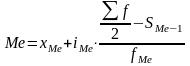
где
хМе
– нижнее значение медианного интервала;iМе
– размер медианного интервала;f
– сумма частот;SМе–1
– сумма частот, предшествующих медианной
частоте;fМе
– медианная частота.Медианному интервалу
соответствует медианная частота. Таким
интервалом будет интервал, сумма
накопленных частот которого равна или
превышает половину суммы всех частот.
15.Понятие вариации признаков и методы измерения её показателей.
Вариация-изменение величины признаков при переходе от 1 объекта ,от 1 случая к другому.
. Ср. вел.дают обобщ. х-ку варьир. признака, но в них не отраж. степ. колеблемости отд. знач-й признака вокруг ср. ур-ня. Для измер. колеблемостиизуч. признака в ст-кепримен. различ. пок-ли.
1. Размах вар-ции (R):R = хмах – хmin,где хmin – minзнач-е призн.;
хmах – maxзнач-е призн.
2.
Ср. лин. отклон.
:
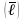пр.:
;
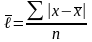взв.:
.
3. Дисп. призн. (σ2):
пр.:
,
взв.:
.
4.
Ср. квадратич. отклон.
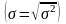
пр.:
;
взв.:
.
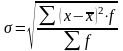5. Коэф. вар-ции (V):
.
24.Тенденция развития в рядах динамики и методы ее выявления. Понятие экстраполяции и интерполяции рядов динамики.
Одной из задач, решаемых с помощью рядов динамики, является выявление закономерностей изменения явления, определение общей тенденции его развития (тренда). Это может быть тенденция к росту, стабильности или снижению. Общая тенденция не всегда четко прослеживается в исходном динамическом ряду с первичными данными, особенно в тех случаях, когда уровни ряда сильно колеблются, то повышаясь, то понижаясь. Поэтому ряд динамики обрабатывают таким образом, чтобы сгладить колеблемость его уровней.
Выявление основной тенденции развития (тренда) называется в статистике выравниванием временного ряда, а методы выявления основной тенденции – методами выравнивания.
Методы, применяемые для выявления основной тенденции развития, можно разделить на две группы:
• методы механического сглаживания;
• методы аналитического выравнивания.
К первой группе относятся простые приемы укрупнения временных интервалов и расчета скользящей средней, ко второй – более сложные методы, основанные на геометрическом представлении динамических данных и использовании надежных теоретических моделей тренда.
Самым простым приемом является укрупнение интервалов времени, к которым относятся уровни динамического ряда (например, суточные – в декадные или месячные, месячные – в квартальные или годовые, квартальные – в годовые), и исчисление по ним средних уровней. Новый динамический ряд, состоящий из средних уровней, даст возможность проследить общую тенденцию развития.
Другим приемом выявления общей тенденции развития является сглаживание с помощью скользящей средней. Для определения скользящей средней формируются интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получают, постепенно сдвигаясь от начального уровня динамического ряда на один уровень. Тогда первый интервал будет включать уровни у1, у2, …, уn, второй – уровни у2, у3, …, уn+1 и т. д. Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице.