§3. Методические рекомендации по обучению учащихся решению уравнений в 7 – 9 классах

На основе изучения способов решения алгебраических уравнений были разработаны методические рекомендации. Данные методические рекомендации включают направленность целей обучения на углубление знаний; на развитие математической культуры учащихся; на формирование умения решать задачи математики, физики, экономики. Это определяет задачи обучения:

• развитие логического мышления школьников, алгоритмической культуры, критического мышления детей на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в профильном классе;

• предоставление разностороннего, развивающего учебного материала, направленного на развитие навыков самостоятельного приобретения знаний;

• содействие наиболее полному развитию творческого потенциала личности.

Программа элективного курса «Решение алгебраических уравнений»

Содержание курса

Тема 1. Основные понятия курса. Операции над многочленами от одной переменной. Определение понятия многочлена. Действия над многочленами: сложение, вычитание. Деление многочлена на многочлен с остатком и без остатка. Теорема Этьена Безу [25].

Тема 2. Различные методы разложения многочлена на множители: вынесение общего множителя, применение формул сокращенного умножения, выделение полного квадрата, группировка, метод неопределенных коэффициентов, подбор корня многочлена по его старшему и свободному коэффициентам, метод введения параметра, замена переменных.

Тема 3. Алгебраические уравнения высшей степени. Квадратные уравнения. Историческая справка. Определение алгебраического уравнения n-ой степени, определение степени уравнения.

Тема 4. Решение алгебраических уравнений с помощью разложения левой части уравнения на множители. Применение различных методов разложения многочлена на множители.

Тема 5. Однородные алгебраические уравнения. Определение однородного алгебраического уравнения, примеры решения однородных алгебраических уравнений.

Тема 6. Возвратные алгебраические уравнения. Определение возвратного алгебраического уравнения, примеры решения возвратных алгебраических уравнений.

Тема 7. Симметрические алгебраические уравнения. Определение симметрических алгебраических уравнений третьей и четвертой степеней, примеры решения симметрических алгебраических уравнений.

Тема 8. Решение систем уравнений с двумя неизвестными, способы решения систем уравнений: сложения, подстановки, введение новой переменной и другие искусственные способы решения систем уравнений.

Тема 9. Обобщение изученного материала. Создание мультимедийных презентаций по изученному материалу (групповые формы работы).

Тема 10. Зачетное занятие.

Тематическое планирование

Тема	Количество часов
1. Основные понятия курса. Операции над многочленами от одной переменной	2
2. Различные методы разложения многочлена на множители	2
3. Алгебраические уравнения высшей степени	1
4. Применение разложения многочлена на множители к решению уравнений	2
5. Однородные алгебраические уравнения	1
6. Возвратные алгебраические уравнения	2
7. Симметрические алгебраические уравнения	2
8. Решение систем уравнений с двумя неизвестными	2
9. Обобщение изученного материала	1
10. Зачетное занятие	1
Всего:	16

Представленные ниже задания для контроля знаний и умений должны помочь учащимся проверить свои знания, способствовать успешному освоению способов решения уравнений.

Задания для контроля

Тест [26]

1. Квадратным уравнением называется уравнение вида ______________ где______– переменная,________– некоторые числа, причем не равен 0.

2. Уравнение вида называется _____________ квадратным уравнением.

3. Для уравнения , если >0, то уравнение имеет _______ корня, если <0, то уравнение __________

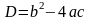4. Выражение называют__________ квадратного уравнения.

5. Если D>0, то квадратное уравнение имеет ____ корня, если D=0, то x= _____

6. Сумма корней приведенного квадратного уравнения равна ______, а произведение корней равно __________

Теоретические вопросы для контроля знаний [27]

1. Определение многочлена.

2. Определение степени многочлена.

3. Алгоритм деления многочлена на многочлен «уголком».

4. Формулировка и доказательство теоремы Этьена Безу.

5. Методы разложения многочлены на множители: вынесение общего множителя, применение формул сокращенного умножения, выделение полного квадрата, группировка, метод неопределенных коэффициентов, подбор корня многочлена по его старшему и свободному коэффициентам, метод введения параметра, замена переменных.

6. Понятие алгебраического уравнения n-ой степени.

7. Определение однородного алгебраического уравнения.

8. Возвратные алгебраические уравнения.

9. Симметрические алгебраические уравнения.

10. Понятие системы уравнений с двумя неизвестными.

11. Способы решения систем уравнений с двумя неизвестными.

Практические задания для контроля знаний

Задание 1. Выполните деление многочлена Р (х) на многочлен Q (x) [28]:

а ) Р (х) = х²+3х+4, Q(x)= х-2;

б) Р (х) = 4х²-х-1, Q(x) = х+3;

в) Р (х) =6х³ +3х² -4х + 3, Q(x) = 2х+1;

г) Р (х) = 9х³ + 9х²- 13х – 6, Q(x) = 3х+1.

Ответы: а) Р (х) = (х +5)Q(x) + 14; б) Р (х) = (4х – 13)Q(x) + 38; в) Р (х) = (3х² -2)Q(x) + 5; г) Р (х) = (3х² + 2х – 5)Q(x) – 1.

Задание 2. Найти остаток r от деления многочлена Р (х) на х-а, если [29]:

а) Р (х) = х⁴-2х³-х², а=3;

б) Р (х) = х⁵+3х⁴-8, а = -2;

в) Р (х) = 7х³⁰ +х¹⁵ +х⁷, а = -1;

г) Р (х) = 4х⁴¹ – х³⁹ +3, а =1.

Ответы: а) r =18; б) r =8; в) r =5; г) r =6.

Задание 3. Выяснить является ли число а корнем многочлена Р (х), если:

а) Р (х) = 3х⁵ – 5х⁴ +х³ -3, а = 2;

б) Р (х) = 2х⁴ +5х³ -2х² -9, а = -3;

в) Р (х) = 2х⁵ – 3х⁴ + 3х³ – х² – 4х +2, а = ;

г) Р (х) = х⁶ -3х⁵ +5х⁴ –х³ +1, а = -2.

Ответы: а) нет; б) да; в) да; г) нет.

Задание 4. Разложить многочлен Р (х) на множители, если известно, что а – корень этого многочлена

а) Р (х) = х³ +5х² +11х +7, а = -1;

б) Р (х) = 2х³ -13х² +18х -15, а = 5;

в) Р (х) = 3х³ +10х² +4х +3, а = -3;

г) Р (х) = х³ -8х² +8х -7, а = 7.

Ответы: а) (х +1) (х² +4х + 7); б) (х – 5) (2х² – 3х + 3); в) (х + 3) (3х² + х + 1);

г) (х – 7) (х² – х + 1)

Задание 5. Найти такое число с, чтобы многочлен Р (х) = х⁵ –х⁴ +сх³ делился на цело на:

а) х+4; б) х – 5; в) х – 6; г) х + 7.

Ответы: а) - 20; б) - 20; в) - 30; г) 56.

Задание 6. Остаток от деления многочлена Р (х) на х – 2 равен 6, а остаток от деления его на х + 3 равен 1. Найти остаток от деления этого многочлена на (х – 2) (х + 3).

Ответ: а =1, в = 4, r = x + 4.

Задание 7. Разложить на множители многочлен [30]

а) х⁴ – 5х³ +7х² -5х +6; б) (х – 4)⁴ + (х + 2)⁴;

в)(4х - 3)³ – (2х - 1)³; г) х⁶ - 1.

Ответ: а) (х - 2) (х – 3) (х² + 1); б) 2 (х² – 2х + 28 - 18 ) (х² – 2х + 28 + 18 ); в) (2х - 2) (28х² – 38х + 13); г) (х - 1) (х² + х + 1) (х + 1) (х² – х + 1).

Задание 8. Разложить на множители многочлен с двумя переменными:

а) х² -3ху +2у²; б) 2х² -7ху +5у² – 3х +3у;

в) х⁴ +4у⁴; г) (x + y + z)³ – x³ – y³ – z³.

Ответ: а) (х – у) (х – 2у); б) (2х -5у – 3)(х – у); в) (х²- 2ху + 2у²)(х² + 2ху + 2у²);

г) 3(х + у) (х + z)(z + у).

Задание 9. Решить уравнение

а) х (х – 1) (х – 2) (х – 3) = 24; Ответ: 4; -1.

б) 2х⁴ + 3х³ – 3х² – 3х +2 = 0; Ответ: х₁ = 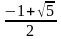, х₂ = , х₃ = ,

х₄ = .

в) 3х⁴ - 2х³ + 4х² - 4х + 12 = 0; Ответ: не имеет корней.

г) х⁸ – х⁶ + х⁴ –х² + 1 = 0; Ответ: нет решений.

д) х⁹ + х⁶ =0; Ответ: 0; -1.

е) 4х⁵ + 4х⁴ - 13х³ -6х² + 9х + 2 =0; Ответ: х_1,2 = ± 1, х₃ = -2, х_4,5 = (1 ± ).

ж) х⁴ +5х³ +8х² +5х + 1 =0; Ответ: -1; - ± .

и) (х² +2х -5)² + 2(х² +2х -5) -5 = х; Ответ: х₁ = , х₂ = , х₃ = , х₄ = .

к) х³ + 2х² – 7х – 12 =0; Ответ: -3; .

л) 3х⁴ – 2х³ -9х² -4х +12 =0; Ответ: 1; 2.

м) 2 (х² +х +1)² – 7 (х -1)² = 13 (х³ -1); Ответ: 2; 4; -1; - .

н) х³ + 4ху² -5у³ =0; Ответ:(t; t), где t- любое действительное число.

о) 2х³ -5х²у +2ху² =0. Ответ: (0; t), (t; 2t), (2t; t), где t – любое действительное число

Задание 10. Решить систему уравнений [31]

а) х–у =1,

х³ -4ху - 4х + 3у +5 =0; Ответ:(2; 1), (1 + ; ), (1 - ; - ).

б) х – у = 3,

х⁴ +6х²у +8у² =0; Ответ: (2;-1), (-6; -9), (-1 +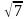 ; -4 + ), (-1 - ; -4 - ).

в) х³ + у³ =19,

х²у + ху² = -6; Ответ: (3; -2), (-2; 3).