Оглавление

Введение 1

§1. Основные понятия линии уравнений курса алгебры 7 – 9 классов 4

§2. Типы преобразований уравнений и методы их решения 21

§3. Методические рекомендации по обучению учащихся решению уравнений в 7 – 9 классах 27

Заключение 35

Список литературы 36

Введение

В системе образования математика занимает одно из центральных мест, что говорит об уникальности данной области знаний.

Зачем нужна математика? Этот вопрос часто задают учителям дети. И каждый раз ответ будет разным в зависимости от уровня развития ребенка и его образовательных потребностей.

А.Н. Колмогоров писал: "Математика не просто один из языков. Математика - это язык плюс рассуждения, это как бы язык и логика вместе. Математика - орудие для размышления. В ней сконцентрированы результаты точного мышления многих людей. При помощи математики можно связать одно рассуждение другим… Очевидные сложности природы с ее странными законами и правилами, каждое из которых допускает отдельное очень подробное объяснение, на самом деле тесно связаны. Однако, если вы не желаете пользоваться математикой, то в этом огромном многообразии фактов вы не увидите, что логика позволяет переходить «от одного к другому» [1].

Математика позволяет сформировать определенные формы мышления, необходимые для изучения окружающего нас мира.

Очень большое влияние оказывает изучение математики на формирование различных форм мышления: логического, пространственно-геометрического, алгоритмического. Любой творческий процесс начинается с формулировки гипотезы. Математика учит мыслить и рассуждать.

Это большой список причин, в силу которых математические знания должны стать неотъемлемой частью обшей культуры и обязательным элементом в воспитании и обучении ребенка.

Линия уравнений имеет особую роль в курсе алгебры и в курсе всей школьной математики. Изучение алгебраических уравнений и способов их решений прочно вошло в систему общей математической подготовки.

Актуальность темы курсовой работы заключается в том, что изучение школьниками уравнений в 7 – 9 классах подготавливает их к более успешному изучению алгебраического материала в 10 – 11 классах. Алгебраические уравнения являются одним из средств моделирования изучаемых фрагментов реальности, и знакомство с ними является существенной частью математического образования.

Итак, цель курсовой работы – разработать методические рекомендации для учителей по обучению учащихся решению алгебраических уравнений в 7 – 9 классах.

Задачи:

1. Провести обзор методической литературы, методических пособий, учебников, методических разработок по данной теме.

2. Выявить наиболее общие подходы к решению алгебраических уравнений.

3. Сформировать понимание основных методов решения алгебраических уравнений.

4. Разработать методические рекомендации по обучению учащихся 7 – 9 классов решению уравнений.

§1. Основные понятия линии уравнений курса алгебры 7 – 9 классов

В курсе алгебры 7 – 9 классов уравнениям отводится значительное место. По мере того как вводят новые виды выражений и изучаются тождественные преобразования этих выражений, расширяется круг рассматриваемых уравнений.

Ниже приведена классификация нелинейных уравнений (рис 1) [2].

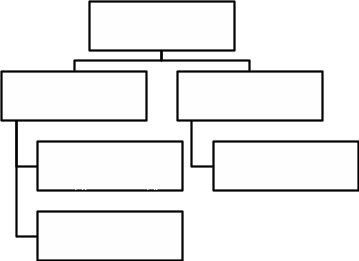
Рисунок 1. Классификация нелинейных уравнений.

Как видно, все уравнения можно разделить на алгебраические и трансцендентные.

Уравнения вида  , где f_n(x) – многочлен одной переменной, называются алгебраическими уравнениями [3]. 

Рассмотрим этапы изучения алгебраических уравнений в школьном курсе математики [4].

1 этап – пропедевтический (1 – 4, 5 – 6 классы).

1 – 4 классы: обозначение неизвестных компонентов действий через переменную и отыскание их на основе свойств действий.

5-6 классы: решение линейных уравнений, решение текстовых задач с помощью линейных уравнений.

2 этап – основной (7 – 9 классы).

7 класс:

• Вводится четкое определение уравнения;

• Теоретически обосновываются свойства уравнений;

• Дедуктивное обоснование процесса решения уравнения;

• Решение систем уравнений;

• Использование графического метода решения.

8 класс:

• Вводится определение неравенства;

• Теоретически обосновываются свойства неравенств;

• Решение систем линейных неравенств с одной переменной;

• Квадратные уравнения и неравенства;

• Рациональные уравнения и неравенства.

9 класс:

• Целое уравнение и его корни;

• Решение уравнений 3-й и 4-й степеней;

• Уравнение с двумя переменными;

• Системы уравнений второй степени с двумя неизвестными.

3 этап – завершающий (10 – 11 классы).

Показательные и логарифмические уравнения и их системы, тригонометрические уравнения, тригонометрические неравенства, показательные и логарифмические неравенства.

Для того, чтобы подробнее раскрыть структуру содержания данной темы и увидеть логику построения линии уравнений в школьном курсе математики, проведем логико – дидактический анализ.

Логико – дидактический анализ темы «Уравнения и неравенства»

7 класс Таблица 1. Логико – дидактический анализ.

Понятие	Алгоритм	Утверждение
Стр.27 н. о. Уравнение [5] Правая часть уравнения; Левая часть уравнения: Член уравнения; Стр.28 н. о. Корень уравнения ; Стр.147 н. Линейное уравнение с двумя неизвестными; Стр.148. н .о. Система двух уравнений; Решение системы двух уравнений с двумя неизвестными; Стр. 154 н. Способ алгебраического сложения	1.Алгоритм решения уравнений сводящихся к линейным. 2.Решение системы двух уравнений способом подстановки. 3.Решение системы двух уравнений способом алгебраического сложения. 4.Решение системы двух уравнений графически. 5.Решение задачи с помощью системы уравнений	1.Решить уравнение-это значит найти все его корни или установить, что их нет. 2.Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный. 3.Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю. 4. Решить систему уравнений- это значит найти все ее решения или установить, что их нет.

Упражнения с равенствами:74,81,82

Решить уравнение:86-94

Решение задач с помощью уравнений:101-115

Решить систему уравнений: 627-632

Способом алгебраического сложения решить систему уравнений: 633-640

Построить график уравнения: 642

Решить графически систему уравнений: 644,645

Решить задачи с помощью систем уравнений: 653-670

8 класс Таблица 2. Логико – дидактический анализ.

Понятие	Алгоритм	Утверждение
Стр.3 Положительное рациональное число [6]; Отрицательное рациональное число; Рациональное число; Стр.10 Неравенство; Стр.11 Сравнить числа; Стр.23 Неравенство с одним неизвестным; Стр.24 Решить неравенство; Решение неравенства; Стр.32 Система неравенств; Система линейных неравенств с одним неизвестным; Стр.33 Решить систему неравенств; Решение системы неравенств с одним неизвестным; Стр.42 Модуль Стр.108 Квадратное уравнение; Стр.111 Неполное квадратное уравнение Стр.122. Приведенное квадратное уравнение Стр.125. Квадратный трехчлен Стр.128 Биквадратное уравнение Стр.174 Квадратное неравенство	1.Метод выделения полного квадрата. 2.Решение квадратного неравенства с помощью графика. 3.Метод интервалов.	1.Если a>b и b˃c, то а>с. 2.Если к обеим частям неравенства прибавить одно и тоже число, то знак неравенства не изменится. 3.Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный. 4.Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится .Если обе части неравенства умножить на одно и тоже отрицательное число, то знак неравенства изменится на противоположный. 5.Если обе части неравенства разделить на одно и тоже положительное число ,то знак неравенства не изменится .если обе части неравенства разделить на одно и тоже отрицательное число, то знак неравенства изменится на противоположный. 6.При сложение неравенств одинакового знака получается неравенство того же знака. 7.При умножение неравенств одинакового знака , у которых левые и правые части положительны получается неравенство того же знака. 8.Любой член неравенства можно перевести из одной части неравенства в другую, изменив знак этого члена на противоположный; при этом знак неравенства не меняется. 9.Обе части неравенства можно умножить или разделить на одно и то же число, не равное нулю; если число положительно, то знак неравенства не меняется, а если число отрицательно, то знак неравенства меняется на противоположный. 10.Уравнение =d,где d˃0, имеет два корня. 11.Сумма корней приведенного квадратного уравнения равна второму коэффициенту ,взятому с противоположным знаком, а произведение корней равно свободному члену. 12.Теорема обратная теорему Виета. 13.если и корни квадратного уравнения +вх+с=0,то при всех х справедливо равенство: +вх+с=а(х- )(х- 14.на множестве комплексных числе уравнение всегда имеет корень.

Задачный материал

Решить уравнение: 16-24

Доказать: 46,45,53

Выполнить сложение неравенств:60

Выполнить умножение неравенств: 61

Решить неравенство:90,91,101-104

Решить систему неравенств: 131-137

Найти модуль: 149

Найти корни уравнения:408

Методом выделения полного квадрата решить уравнение: 429

Решить квадратное приведенное уравнение:450

Решить задачу с помощью уравнения6476-486

Решить систему уравнений:493-497

Решить квадратное неравенство: 660-664

Решить методом интервалов неравенство:675-682

9 класс Таблица 3. Логико – дидактический анализ.

Понятие	Алгоритм	Утверждение
Стр.3 Старший член; Степень многочлена [7]; Нулевой многочлен; Стр.10 Алгебраическое уравнение;	1.Алгоритм деления многочлена уголком. 2.Алгоритм решения рационального уравнения.	1.На множестве комплексных чисел любое алгебраическое уравнение имеет хотя бы один корень.

Задачный материал.

Выполнить деление:2,5

Сократить дробь:13

Решить систему уравнений:25-35

Содержание - понятия, алгоритмы , утверждения.

Средства - учебник, интерактивная доска, презентация, таблицы, карточки

Формы - самостоятельная работа, контрольная работа, индивидуальное задание.

Принципы:

Научности-определения и утверждения.

Активности - фронтальный опрос

Прочности – домашнее задание, актуализация знаний, упражнения для повторения,

Сознательности - исторические справки

Методы:

По источнику знаний – рассказ, беседа.

Наглядности – презентация, таблицы с формулами, карточки с формулами

Практические - практические задания.

Логико – дидактический анализ является системообразующим фактором организации изучения учащимися линии алгебраических уравнений в школьном курсе математики.

В учебниках, рекомендованных Министерством образования и науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2015/2016 учебный год, существуют разные подходы к изучению уравнений. Для сравнения рассмотрим следующие учебники.

Анализ учебников для классов общеобразовательных учреждений

Отметим, что в учебниках Алимова Ш.А. тема «Уравнения» следует за темой «Алгебраические выражения» и изучается в начале учебного года. Понятие уравнения вводится в 7-м классе через сюжетную задачу, как равенство, содержащее неизвестное число, обозначенное буквой. Далее дано определение корня уравнения, как значение неизвестного, при котором уравнение обращается в верное равенство, и на примерах показано, что количество корней может быть разным. Так же вводится понятие решить уравнение (найти все его корни или установить, что их нет), на интуитивном уровне вводится понятие линейного уравнения, так как оно не получает явного определения, а заменяется описанием и иллюстрацией несколькими примерами.

Далее, в теме «Решение уравнений с одним неизвестным, сводящихся к линейным», вводятся свойства уравнений (о переносе членов уравнения и умножении их на одно и то же, неравное нулю число), и тем самым учащимся обосновывается известный из курса математики V-VI классов способ решения уравнений, много времени уделяется изложению правил последовательного преобразования уравнения.

Для закрепления данной темы приводятся задачи:

1. на оперирование основными понятиями;

2. на овладение алгоритмом решения уравнений данного класса;

3. на применение уравнений к решению текстовых задач.

Более глубоко данная тема изложена в учебнике Алимова Ш.А. для учащихся 8 классов. Система упражнений включает не только задания на отработку типовых умений, но и задачи повышенной трудности (задачи на доказательство, на составление программ для вычисления значения выражения, системы уравнений с двумя неизвестными, где одно из уравнений третьей степени, текстовые задачи на движение, задача Маклорена). В данном курсе изучаются квадратные уравнения, неполные квадратные уравнения, уравнения вида , где > , приведённые квадратные уравнения, формулы для нахождения корней данных уравнений, теорема Виета и обратная теорема. Это единственный учебник, в котором подробно изучена тема «Комплексные числа» и их связь с уравнениями – «Квадратное уравнение с комплексными неизвестными».

В учебнике Алимова для учащихся 9 классов есть несколько упражнений на решение иррациональных уравнений. Для решения таких уравнений используется метод возведения в квадрат и координатный метод.

Заметим, что в упражнения для повторения включен отдельный пункт, в который входят упражнения на решение различных видов уравнений и их систем, задачи на составление уравнений. Примечательно то, что более трудные задачи по теме «Уравнения» нашли свое отражение в разделе «Задачи для внеклассной работы».

В учебниках Дорофеева В.Г. понятие уравнения вводится впервые в 6-м классе также через сюжетную задачу. Определение понятия решить уравнение и определение понятия корень не даны, как, впрочем, не сказано о том, сколько вообще корней может иметь уравнение. Данные понятия вводятся лишь в учебнике для учащихся 7 класса.

Дальнейшее изучение темы «Уравнения» продолжается в курсе алгебры 7-ого класса. Учащиеся приобретают навыки решения уравнений в основном при составлении и решении текстовых задач. Однако стоит отметить то, что материал по данной теме не является цикличным – весь необходимый материал изучается отдельными блоками, а блоки структурированы по сложности (от простых уравнений к более сложным).

Система задач в учебниках Дорофеева В.Г. очень разнообразна. Помимо задач на оперирование основными понятиями и задач на овладение алгоритмом решения уравнений при решении текстовых задач (причем не только алгебраическим методом, но и арифметическим), она включает еще и упражнения в чтении и записи алгебраических упражнений, упражнения на истолкование алгебраических выражений для разных условий задачи, упражнения на составление алгебраических выражений и задач по готовым выражениям, кроме того, присутствуют задания тестового характера. Задания повышенной трудности вынесены в пункты под названием «Для тех, кому интересно». Способы решения уравнений аналогичны способам, данным в учебниках других авторов.

В 8-м классе учащиеся решают квадратные уравнения (в том числе неполные и приведенные уравнения), пользуясь приемом выделения квадрата двучлена, методом замены переменной, методом разложения на множители, теоремой Виета. Система задач по теме «Квадратные уравнения» включает разнообразные задачи: задачи на оперирование основными понятиями, задачи на составление уравнений, задачи на заполнение пропусков в уравнении и другие.

В учебнике для учащихся 8 класса находит отражение формула нахождения корней квадратного уравнения с четным вторым коэффициентом (1) и формула нахождения корней приведенного квадратного уравнения (2):

(1)

(2)

Далее учащиеся закрепляют навыки решения уравнений при решении различных систем уравнений и задач.

В курсе 9-ого класса учащиеся решают уравнения с модулем, целые, рациональные, иррациональные, дробные уравнения, уравнения с параметром, задачи на составление уравнений, системы уравнений с двумя переменными. Отметим, что в учебнике для учеников 9 классов для нахождения корня уравнения используется графическое исследование уравнений.

Таким образом, в учебном пособии для учащихся 9 классов охвачен более широкий класс уравнений, чем в учебниках других авторов, а в главу «Повторение» включены все виды уравнений, изученных ранее, а также системы уравнений второй степени.

В учебниках Макарычева Ю.Н. перед введением уравнений с одной переменной изучаются сначала выражения и их преобразования. Понятие уравнения с одной переменной вводится через сюжетную задачу в 7-м классе. Далее дано определение корня уравнения: «Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство» [[4], 23с.]; на примерах показано, что количество корней может быть разным. Так же вводится понятие «решить уравнение – значит найти все его корни или доказать, что корней нет» [[4], 24с.] и равносильные уравнения. Далее рассматриваются линейные уравнения с одной переменной.

Отметим, что система задач включает однотипные упражнения на решение уравнений, почти все они обязательного уровня. Однако, пункт «Дополнительные упражнения» содержит разнообразные задачи повышенного уровня, а, в общем, весь курс алгебры 7-ого класса пронизан уравнениями различной степени сложности.

Отметим также, что в учебнике Макарычева Ю.Н. курс алгебры 7-ого класса начинается и заканчивается темой уравнения. В конце учебного года в главе «Системы линейных уравнений» вводится определение линейного уравнения с двумя переменными и его решения. Система задач в данной главе включает упражнения различной степени сложности на решение уравнений и их систем различными способами.

В пункт «Задачи повышенной трудности» включены параметрические уравнения, уравнения с модулем, целочисленные уравнения, а также задачи на составление систем уравнений и их решение.

В учебнике Макарычева для учащихся 8 класса в главе «Квадратные корни» изучаются уравнения вида , позднее вводится определение квадратного уравнения, формула корней квадратного уравнения, теорема Виета. Система задач включает упражнения на решение квадратных, рациональных, дробно-рациональных и других видов уравнений различными методами, а также упражнения на решение задач с помощью системы уравнений. Отметим, что в учебнике имеется глава «Дополнительные упражнения», в которую включен очень широкий класс задач различной степени сложности на решение уравнений.

Проанализируем учебники Макарычева Ю.Н. (7 – 8), Мордковича А.Г. (8 – 9) и Виленкина Н.Я. (8 – 9), так как данные учебники предназначены для классов с углубленным изучением математики и в них описаны иные подходы к изучению материала и значительно расширено содержание.

В учебнике Макарычева для учащихся 7 классов содержатся 18 параграфов, охватывающих все основные темы общеобразовательного курса алгебры в 7-м классе, и ряд дополнительных вопросов. Учебник дает возможность достаточно обстоятельно рассмотреть теоретические вопросы и предложить учащимся широкий круг упражнений, различных по уровню сложности. Что касается конкретного материала по теме «Уравнения», то он достаточно объемный и содержит упражнения различной степени сложности. В данном курсе изучаются уравнение с одной переменной и его корни, равносильные уравнения, линейные уравнения и уравнения, сводящиеся к линейным, уравнения с модулем и задачи на составление уравнений.

Далее, после изучения глав «Разложение многочленов на множители» и «Формулы сокращенного умножения», продолжается изучение линии уравнений (несмотря на то, что упражнения на решение уравнений различной степени сложности в этих главах также присутствуют) в главе «Системы линейных уравнений». В данной главе для решения предлагаются упражнения на решение уравнений с двумя переменными в целых числах, на решение систем уравнений различными способами (в том числе системы уравнений с тремя переменными) и задачи на составление уравнений.

В учебнике Макарычева для учащихся 8 классов в отличие от учебника для учащихся 7 классов тема «Уравнения» изложена в отдельной главе «Квадратные уравнения», которая изучается в конце курса 8-ого класса. В данной главе также как и в учебниках для классов общеобразовательных учреждений изложен теоретический материал о квадратных уравнениях и его корнях, о решении дробно-рациональных уравнений. Однако изложение достаточно обстоятельно и представлен большой набор разнообразных по тематике и уровню сложности упражнений (например, упражнения на решение параметрических уравнений, уравнений с модулем, на применение обратной теоремы Виета, упражнения на доказательство).

Учебник Мордковича А.Г. (8 кл) отличается, прежде всего, более углубленным изучением соответствующих вопросов курса (изъяты слишком простые примеры и рассуждения, добавлены более сложные и интересные примеры). По оглавлению сразу можно выделить дополнительный материал: алгоритм извлечения квадратного корня, уравнения высших степеней, уравнения с модулями и параметрами. Система задач разнообразна по содержанию и уровню сложности.

Учебник для учащихся 9 классов является продолжением учебника Мордковича для учащихся 8 классов и написан на базе учебника [15]. Единственное отличие заключается во включении в курс дополнительного материала по теме исследования: задачи с параметрами, специальные методы решения систем уравнений (включая системы с тремя, четырьмя переменными), однородные, иррациональные, симметрические системы, системы с модулями. Соответственно и система задач значительно шире.

В учебник Виленкина Н.Я. для учащихся 8 классов включены упражнения на решение дробно-рациональных и кубических уравнений, неопределенных уравнений первой степени, используется метод разложения на множители, формулы сокращенного умножения, метод выделения полного квадрата, основное свойство пропорции, наибольший общий делитель коэффициентов и так далее. Система задач включает уравнения более высокого порядка, так как учащиеся при выполнении заданий могут пользоваться теоремой о делении многочлена на многочлен с остатком, теоремой Безу о корнях многочлена, теоремой о симметрических многочленах от двух переменных. Соответственно и система задач более сложная и трудоемкая. Несмотря на то, что уравнения различной степени сложности включены в каждую тему, рассматриваемую в данном учебнике, они находят свое отражение в отдельной главе «Квадратные уравнения. Системы нелинейных уравнений». В данной главе вводится определение понятия квадратного и приведенного уравнения, корней уравнения, формула нахождения корней через дискриминант и по теореме Виета (в том числе и для многочленов высших степеней). Отметим, что система задач включает упражнения на составление уравнений по известным корням и их кратности, упражнения на решение уравнений с параметрами, упражнения на доказательство, упражнения на нахождение суммы, произведения, разности корней уравнения, не решая данное уравнение, на определение знака корней, задачи на составление уравнений.

Отметим, что в курсе алгебры 8-ого класса учащиеся учатся решать возвратные и однородные уравнения, симметрические системы уравнений и системы уравнений с параметрами и модулем. Помимо методов, известных из курса алгебры общеобразовательной школы, учащиеся при решении уравнений часто прибегают к использованию графического метода решения уравнений.

В учебнике для учащихся 9 классов в систему задач включены иррациональные, показательные уравнения, в том числе с модулем. Достаточно много упражнений на решение уравнений включено в главу «Элементы теории множеств», но также имеется глава, в которой находит свое отражение материал по теме «Уравнения» – «Уравнения, неравенства и их системы». Заметим, что в данной главе, на функциональном уровне даны общее определение уравнения с одной переменной и его корня, определение целого рационального уравнения и методы решения таких уравнений (разложение на множители, введение новой переменной и прочие), определение дробно-рационального уравнения, определение равносильных уравнений. Также как и в курсе алгебры общеобразовательной школы вводятся следствия из уравнений.

Данная глава является итоговой при изучении уравнений в курсе алгебры, так как включает в себя все виды уравнений, изученных не только в курсе 9-ого класса, но и уравнения, рассматриваемые ранее.

Таким образом, анализ программы и школьных учебников позволяет выделить 3 основных блока учебного материала по теме «Уравнения» – теоретический, практический и прикладной. Теоретический блок включает в себя: определение уравнения, корень уравнения, решение уравнения и системы и прочее. Практический блок состоит из умения решать линейные, квадратные, рациональные уравнения, сводящиеся к ним, системы уравнений различными методами. Прикладной блок составляют следующие задачи: решение неравенств и их систем, построение графиков, решение текстовых задач и прочее. Под прикладными умениями в контексте нашего исследования мы понимаем умение решать задачи, в которых уравнения выступают как средство решения.