3.3.3. Ієрархічні кольорові сітки Петрі

Перш, ніж визначити ієрархічну кольорову сітку Петрі введемо наступні поняття.

Визначення 3.1. Перехід t_I у КСП N = (P, T, , F, H, , , ₀) називається джерелом, якщо

pP: F(p, t_I) = 0,

тобто у перехід t_I не входить ні однієї дуги.

Визначення 3.2. Перехід t_S у КСП N називається стоком, якщо

pP: H(t_S, p) = 0,

тобто з переходу t_S не виходить ні одна дуга.

Визначення 3.3. КСП N, що зображується зв’язним графом щонайменше з одним джерелом і з одним стоком, називається блоком.

Визначення 3.4. Зв’язувальною сіткою N_S щодо блока N називають таку КСП, що утворюється з блока N додаванням до нього позиції p₀, яка називається нульовою позицією, і дуг, що ведуть з p₀ в усі джерела і з усіх стоків в p₀. Таким чином, зв’язуюча сітка N_S немає жодного джерела t_I і жодного стоку t_S.

Приклад блока з джерелом t₄, t₆ і стоками t₅ , t₇ і відповідна цьому блоку зв’язуюча сітка зображені на рис. 3.11.

Визначення 3.5. Нульовим маркуванням зв’язувальної сітки N_S блока N називають таке маркування ₀(p₀, ), де в нульовій позиції p₀ є по одному маркеру всіх кольорів, а всі інші позиції порожні; відповідне їй маркування блока називають “порожнім”, тобто

p  N,    : (p, ) = 0;

p  N_S,    p₀  N_S : (p₀, ) = 1.

Визначення 3.6. Блок N називається коректно сформованим, якщо:

- його зв’язувальна сітка N_S при початковому нульовому маркуванні ₀(p₀, ) безпечна в цілому (по всіх кольорах), тобто

p  N_S,    : (p, )  1;

- будь-яка послідовність спрацьованих переходів, яка реалізована в блоці з порожнього початкового маркування ₀(p₀, ), закінчується порожнім маркуванням тільки за умови, якщо кількість спрацювань переходів t_I і t_S однакова;

- як початкові маркування _поч(p, ) використовуються лише такі, для яких мають місце співвідношення:

;

.

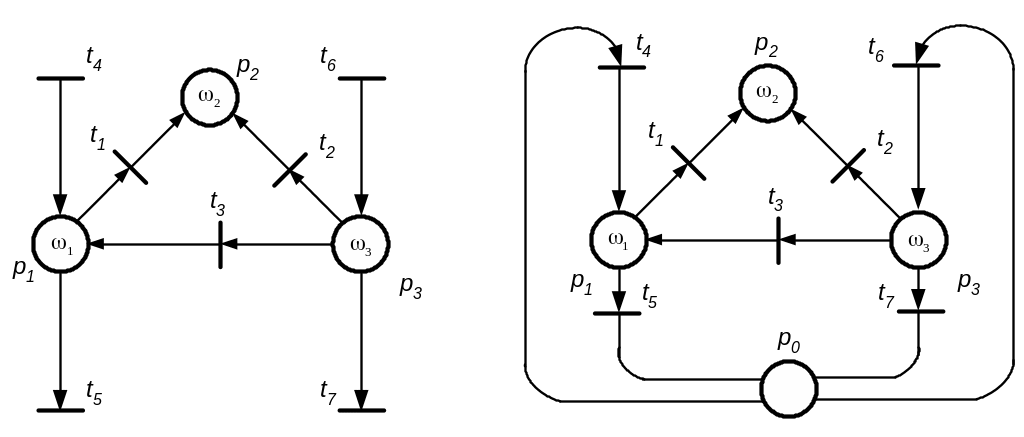Рис. 3.11. Приклади зображення сіток:

а – сітка у вигляді блоку; б – зв’язувальна сітка

Звичайно передбачається, що ніякі два переходи в сітці Петрі не можуть спрацьовувати одночасно.

На відміну від цього, для деяких переходів не тільки допускається одночасне спрацьовування, але, навпаки, забороняється неодночасне спрацьовування. Такі переходи утворюють перехід-зв’язку.

Визначення 3.7. Переходом-зв’язкою називають підмножину переходів , при якій з будь-якої їх вхідної позиції дуга веде тільки в один з переходів, що знаходяться у зв’язці.

Спрацьовування переходу-зв’язки може відбутися тільки тоді, коли порушені усі вхідні в нього переходи.

У сітці Петрі переходи-зв’язки завжди можна замінити простими переходами. Приклад сітки Петрі з переходами-зв’язками та їх заміною простими переходами показаний на рис. 3.12.

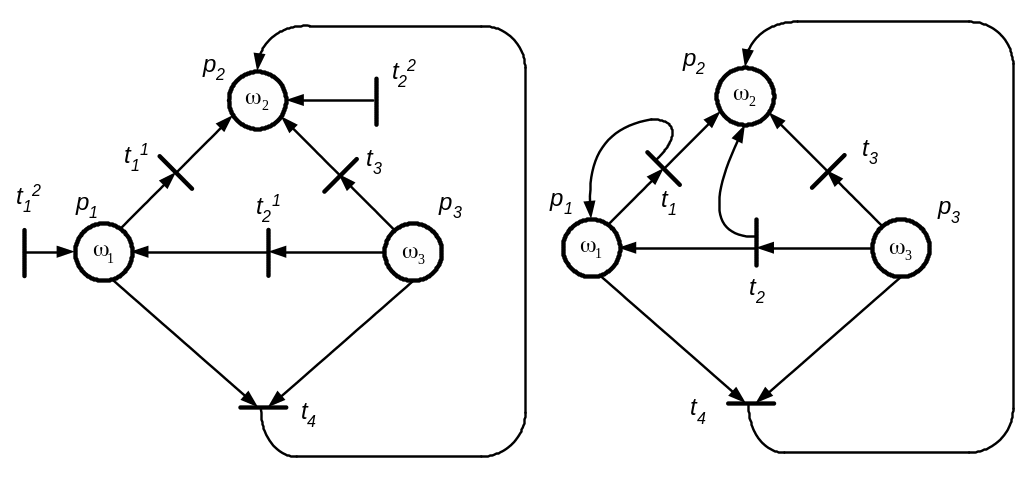
а) б)

Рис. 3.12. Сітка Петрі з переходами-зв’язками (а) і простими переходами (б)

За допомогою переходів-зв’язок легко відображати зв’язки між алгоритмами, підалгоритмами та операторами.

Використовуючи наведені поняття, дамо визначення ієрархічної кольорової сітки Петрі (ІКСП).

Визначення 3.8. Ієрархічною кольоровою сіткою Петрі називається набір , який складається з кінцевої множини коректно сформованих блоків , що частково впорядковано у відповідності з відношення .

Відношення між блоками графічно представляється деревом, кореню якого відповідає старша сітка N₀, що може і не бути коректно сформованим блоком (рис. 3.13, а).

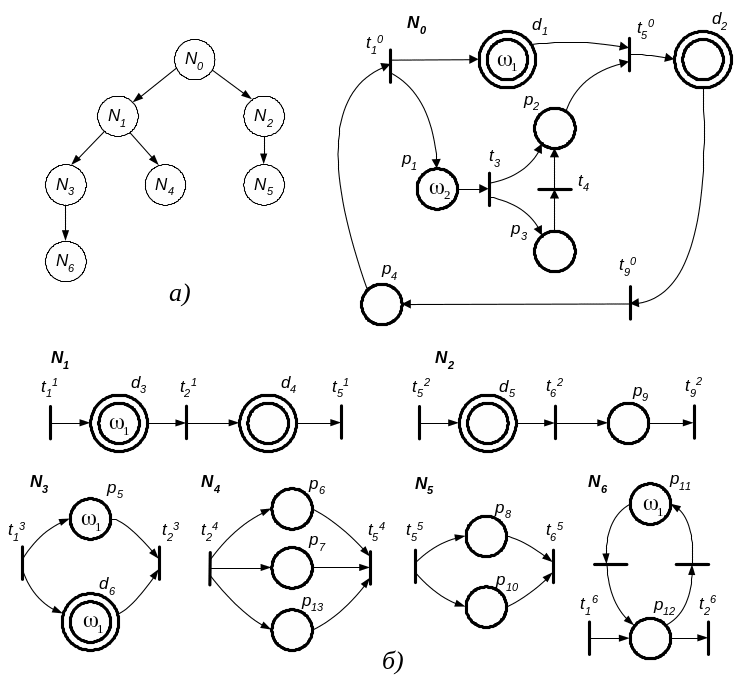
Рис. 3.13. Ієрархічна кольорова сітка Петрі:

а – дерево відношення; б – зображення сітки

Для будь-яких двох сіток N_и і N_v, що відповідають початковій і кінцевій вершинам дуги дерева відношення сітки N^*, присутня особлива позиція d_v  N_и, що називається дублером блока N_v.

Позиція-дублер блока N_v в ІКСП зображається подвійним кругом із символом d_v. Блок N_v дублюється позицією-дублером d_v, що належить тільки сітці N_и. Таким чином, індекси дублера і дублюючого ним блока завжди збігаються. Між вхідними (вихідними) переходами дублера і джерелами (стоками) дублюючого ним блока має місце взаємнооднозначна відповідність. При цьому кожен вхідній (вихідний) перехід дублера і співставлене йому джерело (стік) у дублюючому блоці входять в один перехід-зв’язку.

У старшій ІКСП, показаній на рис. 3.13, б, містяться дублери d₁ і d₂ блоків N₁ і N₂, у блоці N₁ – дублери d₁ і d₄ блоків N₃ і N₄, у блоці N₂ – дублер d₅ блока N₅, у блоці N₃ – дублер d₆ блока N₆.

У ІКСП існують наступні переходи-зв’язки:

причому вхідному переходу дублера d₁ в старшій сітці N₀ співставлене джерело в блоці N₁, а вихідному переходу – стік , вхідному переходу дублера d₃ в блоці N₁ співставлене джерело в блоці N₃, а вихідному переходу – стік і т.д.

Визначення 3.9. Початкові маркування блоків N_i і старшої сітки N₀ в ІКСП N = {N_i} погоджені наступним чином:

- якщо всі позиції дублюючого блока порожні, то в дублері маркер відсутній, тобто

;

- якщо не всі позиції дублюючого блоку порожні, то в дублері знаходиться маркер того ж кольору, що й у дублюючому блоці і, крім цього,

.

Для алгоритмів управління ГВС позиції-дублери ІКСП означають наступне: кожному дублеру відповідає підалгоритм, що є алгоритмом, опис якого задається дублюючим блоком. Якщо в дублюючому блоці міститься свій дублер, то йому також відповідає підалгоритм, але вже більш низького рівня складності, і так доти, поки якому-небудь дублеру не буде відповідати оператор. Співвідношення алгоритмів за складністю визначається деревом відношень: рівень складності підалгоритму тим вищий, чим ближче до кореня дерева знаходиться сітка, яка містить дублер, що відповідає цьому підалгоритму.

Як підалгоритми алгоритму управління ГВС можна виділити алгоритми управління АТСС, роботом-штабелером, автономним транспортним модулем тощо.

Таким чином, ієрархічна сітка Петрі дозволяє у явному вигляді відбивати ієрархію операторів в алгоритмах управління ГВС і використовувати її при описі алгоритмів.

З метою модифікації застосуємо до ІКСП дві операції: заміщення дублера блоком і заміщення вузла дублером.

Операція заміщення дублера блоком полягає в наступному: сітка з дублером, що заміщається, поєднується з дублюючим блоком шляхом заміни відповідних переходів-зв’язок еквівалентними їм простими переходами; з отриманої сітки віддаляється позиція-дублер разом з інцидентними з нею дугами.

Приклад виконання цієї операції наведений на рис. 3.14. Ієрархічна сітка (рис. 3.14, а) після об’єднання сітки, що містить дублер d₁, з дублюючим блоком N₁ перетворюється в сітку, зображену на рис. 3.14, б. Після видалення позиції d₁ та інцидентних їй дуг отримаємо сітку, показану на рис. 3.14, в.

В результаті послідовного заміщення дублерів (у довільному порядку) з вихідної ІКСП виходить проста сітка. Зміст операції заміщення дублера полягає в тому, що, маючи множину операторів у підалгоритмах у вигляді окремих блоків і застосовуючи суперпозицію, можна побудувати алгоритм управління ГВС у вигляді простої сітки Петрі.

Операція заміщення локалізованого вузла є оберненою до операції заміщення дублера і дозволяє з простої сітки Петрі отримати ієрархічну.

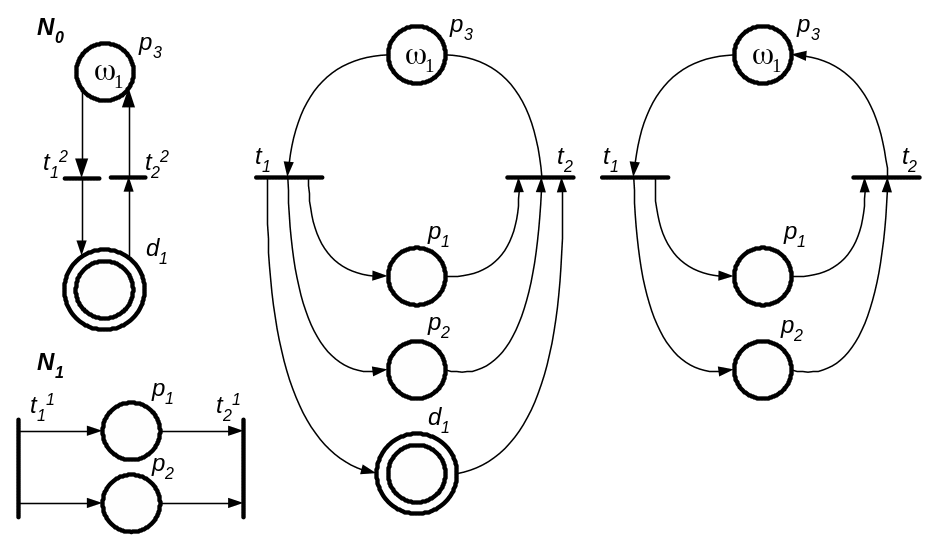
а) б) в)

Рис. 3.14. Ієрархічна сітка (а) і приклад операцій заміщення дублера (б) і вузла (в)