3. Матричне подання.

Матричне подання – це аналітичний спосіб представлення сітки Петрі. У цьому випадку функції інциденцій та початкове маркування зображаються у вигляді матриць розміром [n  m]:

;

та вектором-стовпцем розміром [n  1]:

,

де F_ij = F(p_i, t_j); H_ij = H(t_j, p_i); ₀ = ₀(p_i).

4. Правила роботи сітки Петрі.

Робота (функціонування) сіток Петрі визначається як послідовність спрацьовування переходів, внаслідок яких відбувається зміна маркувань позицій.

Перехід може спрацьовувати, якщо він збуджений.

Перехід t_j вважається збудженим, якщо виконується наступна умова:

,

тобто виконуються доумови здійснення модельованої цим переходом події – у кожній вхідній позиції переходу кількість маркерів не менша кратності дуги, що їх з’єднує (рис. 3.2).

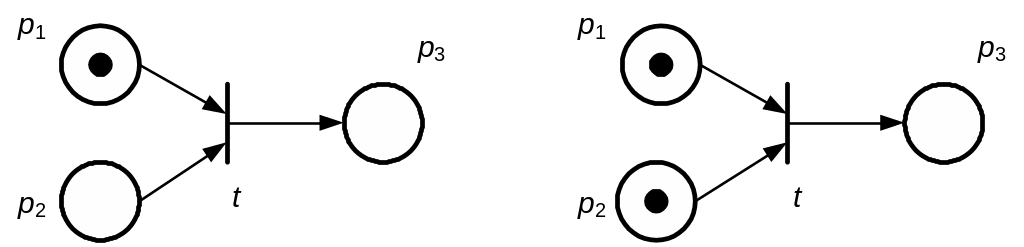
а) б)

Рис. 3.2. Умови збудження переходу: а – умова не виконана; б – умова виконана

Тоді правило спрацьовування збудженого переходу t_j має вигляд:

,

тобто при спрацьовуванні збудженого переходу маркування  замінюється маркуванням  за таким правилом: з вхідних позицій переходу забирається певна кількість маркерів, яка визначається функцією F(p_і, t_j), а вихідні позиції переходу отримують іншу кількість маркерів, яка визначається вже функцією H(t_j, p_і) (рис. 3.3).

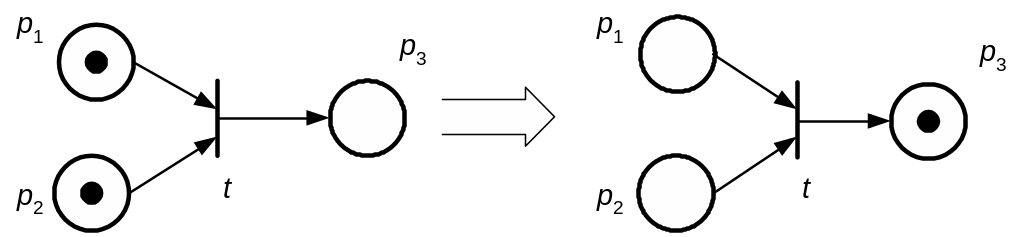
Рис. 3.3. Правило спрацьовування збудженого переходу

Необхідно відмітити, що у випадку використання матричного способу подання сіток Петрі умова збудження переходу t_j має вигляд:

  FU,

а правило його спрацьовування:

  =  + (H – F)U,

де – вектор-стовпець розміром [m  1], у якого всі елементи дорівнюють 0, крім U_j = 1.

У будь-якому стані сітки Петрі може існувати декілька одночасно збуджених переходів. Але послідовність їх спрацьовування не встановлена і може бути будь-якою, але без одночасного спрацьовування переходів. Тому в сітках Петрі визначають декілька прийнятних послідовностей спрацьовувань переходів, що породжують послідовності виникаючих маркувань. Це відображає паралелізм та недетермінізм сіток Петрі.

Таким чином, з функціонуванням сітки Петрі пов’язують дві послідовності:

1) послідовність спрацьовуючих переходів;

2) послідовність виникаючих (досяжних) маркувань.

Ці послідовності є взаємозв’язаними.

Два маркування  і   вважаються безпосередньо досяжними, якщо у функціонуванні сітки існує перехід t_j, спрацьовування якого переводить сітку з  у  (рис. 3.4).

.

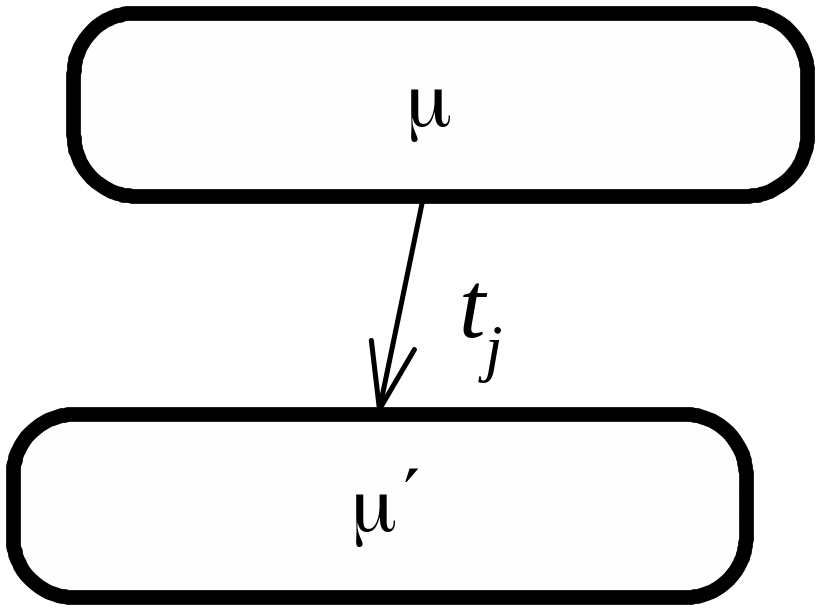
Рис. 3.4. Безпосередньо досяжне маркування

Два маркування  і   вважаються досяжними, якщо у функціонуванні сітки існує послідовність переходів G = (t_j1, t_j2, ..., t_jk), яка переводить сітку з  у  :

   ,

тобто виникає послідовність безпосередньо досяжних маркувань (рис. 3.5):

Рис. 3.5 Послідовність досяжних маркувань

Таким чином, формально функціонування сітки подається:

– мовою сітки Петрі L(N) – множиною послідовностей спрацьовуючих переходів;

– множиною досяжності R(N) – множиною маркувань, досяжних з початкового маркування.

Ці послідовності об’єднуються у рамках єдиної моделі представлення роботи сітки – графа досяжності – орієнтованого графа, вершинами якого є маркування з множини R(N), а дугами – спрацьовуючі переходи з L(N) (рис. 3.6, б). Граф з відсутніми циклами є деревом досяжності (рис. 3.6, а).

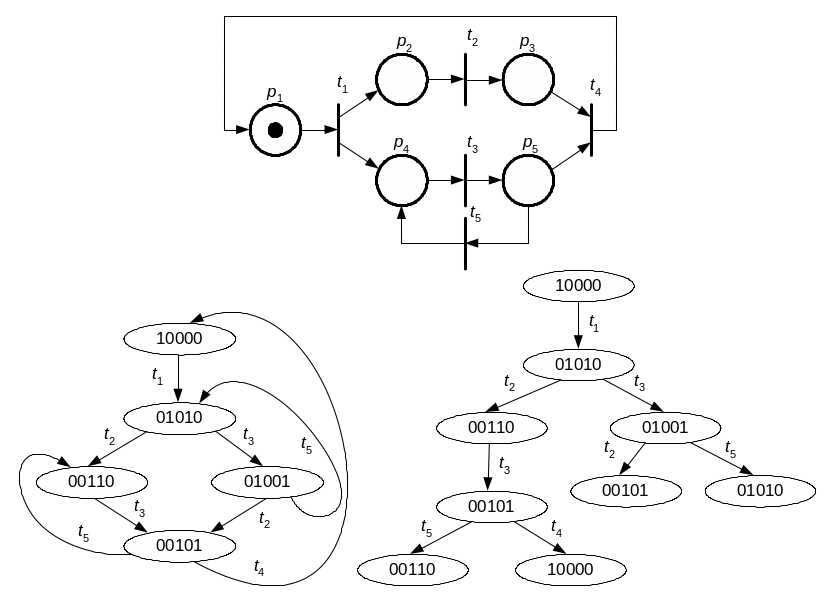
а) б)

Рис. 3.6. Дерево та граф досяжності сітки Петрі:

а – граф досяжності; б – дерево досяжності