Лекция 2

Понятия о системах единиц физических величин.

Понятие об основных и производных единицах. Принципы образования производных единиц. Выражение единиц в десятичных и кратных долях единицах. Эталонная база системы единиц и передача информации от эталона рабочих средствам измерения.

Международная система единиц физических величин.

Международная система единиц физических величин (система СИ): основные, дополнительные производные единицы. Преимущества системы СИ. Определения основных единиц системы СИ. Кратные и дольные единицы. Внесистемные единицы, допускаемые к применению наравне с единицами СИ. Формирование единиц и размерности производных единиц. Эталонная база единиц системы СИ

Методы и средства измерений.

Свойства физических объектов, по которым можно сравнивать их свойства можно разделить на три группы.

1. Отношение эквивалентности. Отношение по которому можно только сравнивать свойства объектов по принципу ”равно — не равно”

2. Отношение порядка. По этому отношения свойства объектов можно сравнивать по принципу “больше — меньше”.

3. Отношения аддитивности. По этому отношению однородные свойства различных объектов могут суммироваться. На этом принципе и построен процесс измерений.

Все физические величины в зависимости от проявлений свойств объектов в отношении эквивалентности, порядка и аддитивности можно разделить на три группы. К четвёртой нгруппе относятся свойства объектов, которые не имеют количественной оценки. Например, классификация животных или перечень химических элементов в Периодической таблице.

1. Экстенсивные величины. Для них определены операции сложения и вычитания, но в результате этих действий получается качественно та же самая величина. Подобные величины: длина, масса, сила тока и т.д.

2. Вторая группа — интенсивные величины, для которых определены отношения поряка и эквивалентности (теплее — холоднее или одинаково тёплые). Лперации сложения или вычитания для таких величин не имеют физического смысла. Но интервалы относятся к величинам первой группы. Единицу измерения они имеют, но их шкалы не имеют естественного нуля. Например шкала звёздных величин, по которой измеряется блеск звёзд и и др. источников излучения. К ним относится также время и электрический потенциал.

3. Третья группа — величины, для которых определены только отношения порядка и эквивалентности (интенсивные величины). Существование подобных соотношений устанавливается теоретически или экспериментально.ример, медь твёрже резины и т.п. К этой группе относятся например, интенсивность землетрясений, силы ветра и др. величины, для измерения которых используются отвлечённые числа или баллы, характеризующие размер величины в соответствии с выбранным измерительным преобразованием.

Измерительное преобразование — вид преобразования, при котором устанваливается взаимно однозначное соответствие между размерами двух величин. Оно осуществляется техническими устройствами — средствами измерений. Преобразуемая величина является измеряемой — входной, а результат преобразования — результатом измерения или выходной величиной. В результате измерения получают:

Значение физической величины — выражение размера физической величины, в виде некоторого числа принятых для неё единиц.

Измерение физической величины – совокупность операций по применению средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения ( в явном или неявном виде ) измеряемой величины с её единицей и получение значения этой величины.

Измерение физической величины выполняют с помощью технических средств. Основное уравнение измерения Q = q*U, где q – число единиц, а U – величина единицы измерения.

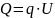
Количественные или качественные проявления любого свойства реальных объектов образуют упорядоченные множества чисел или условных знаков, совокупность которых образует шкалу.

Шкала физической величины — упорядоченная совокупность значений физической величины, служащая исходной основой для измерений данной величины.

Условная шкала физической величины — шкала, исходные значения, которой выражены в условных единицах.

Различают 5 основных типов шкал.

1. Шкала наименований (шкала классификаций). Такие шкалы применяют для свойств, проявляющих себя только в отношении эквивалентности. При этом качественным свойствам объектов приписывается наименование или число. Измерительное преобразование для таких шкал не найдено либо не требуется по условиям исследования данного объекта. Например, шкала цветов. Часто такие шкалы применяются для экспертных оценок

2. Шкала порядка (шкала рангов). Применяется для оценивания величин 3-й группы, которые проявляютсвои свойства в отношении эквивалентности и порядка по возрастанию или убыванию. В этих шкалах установлен нуль-пункт, но единицы не вводится, так как не установлена линейность изменения размеров величины относительно выбранного измерительного преобразования. Может быть использована условная шкала с нанесёнными на неё опорными точками, например, шкала твёрдсти минералов (тальк — 1, гипс — 2, …, 7 — кварц, …, 10 — алмаз).Промежуточных значений здесь нет. Шкала условна. Может быть подобрано измерителтное преобразование. Например, шкала твёрдости по Бринелю (вдавливание шарика) или Роквеллу (вдавливание пирамидки). Вдавливание происходит с постоянным усилием, а по размеру отпечатка судят о твёрдости материала. Зависимость в этом случае есть, но она нелинейна.

3. Шкала интервалов (шкала разностей). Эти шкалы применяются для измерений интервалов величин 2-й группы. Она состоит из одинаковых интервалов, следовательно линейна и им еет единицу измерения. Нуль такой шкалы принят по соглашению и является условным. К таким шкалам относят временнЫе шкалы, температурные (Цельсия или Фаренгейта) и др. Шкала звёздных величин также относится к таким шкалам.

4. Шкала отношений. Эти шкалы являются физическими и имеют единицу измерения и естественный нуль пункт шкалы. Размер величины Q описывается уравнением измерения (см. выше). С помощью таких шкал измеряются физические величины первой группы, для которых определены все арифметические операции. Такие шкалы измеряют массу, длину, силу тока, напряжение и др.

5. Абсолютные шкалы. Вводятся для физических величин, для которых справедливы отношения эквивалентности, порядка и аддитивности, но дополнительно имеющих естественное определение единицы измерения, не зависящее от принятой системы единиц. Эта единица — безразмерная. Например, плоский или телесный угол, некоторые относительные величины, как коэффициент усиления (ослабления) и т.п.