Другие алгоритмически неразрешимые задачи

Упомянутая в начале статьи проблема проверки правильности любых математических утверждений также оказалась алгоритмически неразрешимой. Сформулируем ее формально в более общем виде.

Пусть у нас есть посылка Rи следствиеS, записанные в виде слов (формул) в некотором алфавите, состоящем из букв, цифр, скобок, знаков математических и логических операций. Процесс вывода следствияSиз посылкиRможет быть описан путем указания последовательности допустимых формальных преобразований слов (дедуктивной цепочки).

Проблему распознавания выводимостиможно сформулировать следующим образом:Существует ли для любых двух слов R и S дедуктивная цепочка, ведущая от R к S? Решение понимается в смысле существования алгоритма, дающего ответ на этот вопрос для любых словR и S. В 1936 г. американский математик Черч доказал теорему о том, что проблема распознавания выводимости алгоритмически неразрешима. Тем самым выяснилась причина безуспешности всех прошлых попыток решения задачи, поставленной Лейбницем.

Неразрешимой оказалась и так называемая “10-я проблема Гильберта”. В упрощенной формулировке она звучит так: требуется выработать алгоритм, позволяющий для любого алгебраического уравнения P(x₁,x₂, …,x_n) = 0, гдеP— многочлен с целыми коэффициентами, выяснить, имеет ли оно целочисленное решение. В 1970 г. советский математик Ю.В. Матиясевич доказал невозможность построения алгоритма для решения этой задачи. Интересно, что если для конкретного уравнения известно, что решение в целых числах есть, то алгоритм отыскания этого решения существует.

Какие методы используются для доказательства алгоритмической неразрешимости? Обычно неразрешимость новых задач доказывается методом сведенияк этим задачам известных алгоритмически неразрешимых задач. Тем самым доказывается, что если бы была разрешима новая задача, то можно было бы решить и заведомо неразрешимую задачу. Применяя метод сведения, обычно ссылаются на искусственные задачи, которые не представляют самостоятельного интереса, но для которых легко непосредственно доказать их неразрешимость, например, описанную выше проблему самоприменимости.

3. Алгоритмические конструкции Виды алгоритмических конструкций

Для записи алгоритмов существуют разные способы (см. “Способы записи алгоритмов”): текстово-формульная запись, блок-схема, машина Тьюринга, машина Поста, программа на алгоритмическом языке и др. Каждый алгоритм записывается в системе команд исполнителя. Вне зависимости от выбранной формы записи элементарные шаги алгоритма объединяются валгоритмические конструкции(структуры):последовательные, ветвящиеся, циклические, вспомогательные алгоритмы (см.“Подпрограммы”)и рекурсивные. В 1966 году Бом и Джакопини доказали, что для записи любого сколь угодно сложного алгоритма достаточно трех основных алгоритмических конструкций: последовательных, ветвящихся, циклических.

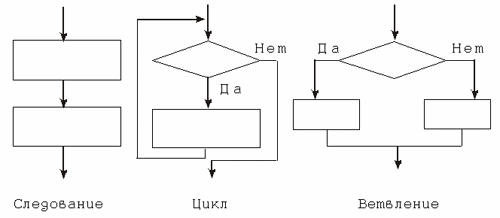
Алгоритм P(или его часть) реализован черезпоследовательную алгоритмическую конструкцию (следование), если каждый шаг алгоритма выполняется один раз, причем после каждогоi-го шага выполняется (i+ 1)-й шаг, еслиi-й шаг—не конец алгоритма. Такой алгоритм или часть алгоритма еще называютлинейным.

 

Пример 1.Линейным является алгоритм перевоза через реку Волка, Козы и Капусты, при условии, что в лодке можно перевозить только один из указанных объектов, а на берегу вместе не могут находиться Коза и Волк, а также Коза и Капуста:

1) перевези Козу;

2) вернись на исходный берег;

3) перевези Волка;

4) вернись на исходный берег с Козой;

5) перевези Капусту;

6) вернись на исходный берег;

7) перевези Козу.

Алгоритм Pреализован с использованиемветвящейся алгоритмической конструкции (ветвления), если на каком-либо шаге последовательное выполнение алгоритма прерывается, и выбор следующего шага определяется входными данными алгоритма.Ветвлениезадает выполнение либо одной, либо другой группы операторов в зависимости от выполнения какого-либо условия (в зависимости от истинности или ложности соответствующего логического выражения, см. “Логические выражения”). Затем исполнение алгоритма выходит на общее продолжение. Для конкретных входных данных ветвящаяся алгоритмическая конструкция сводится к последовательной алгоритмической конструкции. Ветвление бывает полным и неполным. В случае неполного ветвления при невыполнении условия никакие действия не выполняются.

Пример 2. Запишем в словесной форме алгоритм решения уравненияax²+bx+c= 0, гдеa, b,c— произвольные действительные числа, аx— искомая величина. Еслиa0, то для нахождения корней используются известные формулы, при этом существование корней зависит от знака дискриминанта квадратного уравнения. Еслиa= 0, то уравнение становится линейным. Однако приb= 0 оно вырождается в равенствоc= 0. Поэтому, еслиcдействительно равно 0, то все действительные числа являются корнями такого уравнения, в противном случае — корней нет. Ниже приведена блок-схема данного алгоритма.

Алгоритм Pреализован с использованиемциклической алгоритмической конструкции, если некая, подряд идущая группа шагов алгоритма, выполняется несколько раз. Количество повторений либо фиксировано, либо зависит от входных данных алгоритма. Любая циклическая алгоритмическая конструкция содержит в себе элементы ветвящейся алгоритмической конструкции: после очередного выполнения группы шагов, входящих в цикл (которое называетсяшагом цикла, илиитерацией), проверяется некоторое условие, формируемое в процессе вычислений. В зависимости от значения этого условия цикл либо завершается, либо начинается выполнение следующего шага цикла.

В качестве примера алгоритма с циклической конструкцией можно рассмотреть алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел (см. “Алгоритм”).

Следование, ветвление и цикл называют базовыми конструкциями структурного программирования. Их особенностью является то, что любая из них имеет только один вход и один выход, поэтому они могут вкладываться друг в друга. Например, цикл может содержать следование из двух ветвлений, каждое из которых включает вложенные циклы.