
- •Числовая последовательность.
- •Бесконечно малые и бесконечно большие величины
- •Свойства непрерывных функций
- •Точки разрыва функции и их классификация
- •Экстремумы функции. Необходимое и достаточное условие экстремума.
- •Наибольшее и наименьшее значение функции на отрезке
- •Выпуклость и вогнутость графика функции. Точки перегиба.
- •Асимптоты графика функции
- •Общая схема исследования функции и построение ее графика
- •Первообразная и неопределенный интеграл
- •Матрицы. Умножение матриц.
- •Определитель матрицы
- •Свойства определителя матрицы.
- •Элементарные преобразования с матрицами:
Наибольшее и наименьшее значение функции на отрезке
Наибольшим
значением функции f(x)
на отрезке ![]() называется число М = max
f(x)
такое,
что М
называется число М = max
f(x)
такое,
что М![]() f(x)
для всех x
f(x)
для всех x![]() .
.
Наибольшим
значением функции f(x)
на отрезке
называется число М = min
f(x)
такое,
что М![]() f(x)
для всех x
.
f(x)
для всех x
.
Выпуклость и вогнутость графика функции. Точки перегиба.
Кривая называется выпуклой вверх (выпуклой) на отрезке [a;c), если все точки кривой лежат ниже любой ее касательной на [a;c).
Кривая называется вогнутой вниз (вогнутой) на отрезке (с;b], если все точки кривой лежат выше любой ее касательной на (с;b].
Рисунок
Точка, которая отделяет выпуклость от вогнутости, называется точкой перегиба графика функции.
Т еорема:
Если во всех точках интервала (a;
b):
еорема:
Если во всех точках интервала (a;
b):
а )
f
// (x)
< 0, то график функции на (a;
b)
является выпуклым;
)
f
// (x)
< 0, то график функции на (a;
b)
является выпуклым;
б) f // (x) > 0, то график функции на (a; b) является вогнутым.
Если
в точке x0![]() (a;b)
вторая производная f
// (x)
= 0 или не существует и при переходе через
точку
x0
слева направо меняет знак, то точка x0
является
точкой перегиба.
(a;b)
вторая производная f
// (x)
= 0 или не существует и при переходе через
точку
x0
слева направо меняет знак, то точка x0
является
точкой перегиба.
Рисунок
Асимптоты графика функции
Прямая
x=x0
, параллельная оси OY,
называется вертикальной
асимптотой
графика функции
y=f(x),
если ![]()
Прямая
линия называется наклонной
(горизонтальной) асимптотой
графика функции y=f(x),
если расстояние от произвольной точки
М графика до этой прямой стремится к 0
при неограниченном удалении точки от
начала координат, т.е. ![]() .
.
Формула
наклонной асимптоты y=kx+b,
где k=![]() , b=
, b=![]()
Общая схема исследования функции и построение ее графика
Исследование функции в целях построения графика ведется в следующей последовательности:
Находится область определения функции D(f) и если возможно область допустимых значений E(f);
Находятся точки разрыва функции и промежутки непрерывности;
Устанавливаются промежутки знакопостоянства функции;
Устанавливаются четность, нечетность, периодичность;
Определяются точки пересечения графика с осями координат (нули функции);
Находятся критические точки функции, точки экстремума, экстремумы, промежутки монотонности (возрастание и убывание функции);
Определяются промежутки выпуклости и вогнутости графика функции, точки перегиба;
Устанавливаются асимптоты графика функции;
Строится график функции.
Первообразная и неопределенный интеграл
Функция F(x), определенная на некотором конечном или бесконечном промежутке называется первообразной функцией (или просто первообразной) функции f(x), если:
Функция непрерывна на заданном промежутке;
Во всех внутренних точках х промежутка функция имеет производную и F /(x)=f(x).
Совокупность
всех первообразных функции f(x),
определенных
на некотором промежутке, называется
неопределенным
интегралом
от функции
f(x)
и
обозначается с помощью символа ![]() .
.
![]() ,
где
F(x)
– любая из первообразных функций для
f(x)
на промежутке, а С-
произвольная
постоянная.
,
где
F(x)
– любая из первообразных функций для
f(x)
на промежутке, а С-
произвольная
постоянная.
Простейшие свойства неопределенных интегралов
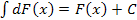 или
или 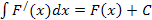
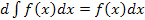
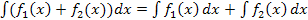
Если k=0 – некоторое число, то

Определенный интеграл
Определенным интегралом от функции y=f(x) на отрезке [a;b] (или в пределах от до) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к 0: (рисунок)
![]()
Если
f(x)>0
на [a;b],
то определенный интеграл геометрически
представляет собой площадь
криволинейной трапеции
![]()
Свойства определенного интеграла

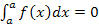
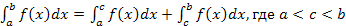
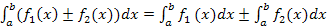 – интеграл суммы равен сумме интегралов
этих функций.
– интеграл суммы равен сумме интегралов
этих функций. – постоянную можно вынести за знак
интеграла.
– постоянную можно вынести за знак
интеграла.
Формула Ньютона-Лейбница
![]()
Геометрические приложения определенного интеграла
Площадь, ограниченная кривой y = f(x), осью OX и прямыми x=a и x=b, где f(x)>0 на [a;b], есть предел, к которому приближается сумма прямоугольников (рисунок)
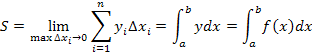
Площадь фигуры, ограниченную кривыми y=f1(x) и y=f2(x) и прямыми x=a и x=b определяют по формуле:
![]()
Объем тела, ограниченного линиями y=f1(x) и y=f2(x) и прямыми x=a и x=b определяют по формуле:
![]()
Матрицы. Действия с матрицами.
Матрица – это прямоугольная таблица каких-либо элементов a i j,
где i – число строк, j – число столбцов.
У каждого числа свое местоположение, и переставлять их нельзя!
Матрицы обозначают прописными латинскими буквами A, B, C…
Когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Например, матрица размером 2×2, 2×3, 1×4
А=
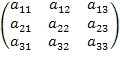 - матрица состоит из 9 элементов, 3 строк
и 3 столбцов
- матрица состоит из 9 элементов, 3 строк
и 3 столбцов
![]() –
единичная матрица – это матрица, сотоящая
из 0 и 1.
–
единичная матрица – это матрица, сотоящая
из 0 и 1.
![]() нулевая
матрица – это матрица, состоящая из 0.
нулевая
матрица – это матрица, состоящая из 0.
Если
в матрице один столбец или одна
строка, то такие матрицы называют векторами:
![]() или
или
![]()
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной (3×3, 2×2).
Действия с матрицами.
Вынесение минуса из матрицы (внесение минуса в матрицу).
Вынесем
минус за пределы матрицы, сменив у
КАЖДОГО элемента матрицы знак:

Умножение матрицы на число.
чтобы умножить матрицу на число (целое или дробное, положительное или отрицательное), нужно каждый элемент матрицы умножить на данное число. Пример:
![]()
Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Пример:
Транспонировать матрицу А= ![]()
Аt
= ![]() –
транспонированная матрица.Сумма
(разность) матриц.
–
транспонированная матрица.Сумма
(разность) матриц.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Для того чтобы сложить (вычесть) матрицы, необходимо сложить (вычесть) их соответствующие элементы:
А±B
=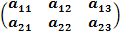 ±
± 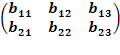 =
= 
