Числовая последовательность.

Если всякому натуральному числу (номеру места) по какому-нибудь закону однозначно поставлено в соответствие определенное число (член последовательности), говорят, что задана бесконечная числовая последовательность.

x₁, x₂, x₃, x₄, x₅, x₆,…., x_n – числовая последовательность.

x_n – n-ый член последовательности.

Последовательность – это частный случай функции. Ее областью определения является множество натуральных чисел. Последовательность можно задать формулой.

Пример:

1. x_n =2n – 1. Вычислим x₁ = 2•1 – 1=1, x₂ = 3, x₃ = 5 …. Т.е. последовательность 1, 3, 5, …

2. x_n = Последовательность 1/3, 2/5, 3/7, ….

Последовательность (n ) называется возрастающей, если для любого натурального n выполняется неравенство . Пример 1.

Последовательность (n ) называется убывающей, если для любого натурального n выполняется неравенство . Пример 2.

Возрастающие и убывающие последовательности называются монотонными последовательностями.

Последовательность называется ограниченной, если существуют два числа m и M такие, что для всех n выполняется неравенство, .

Пример: - ограниченная , т.к. существуют 2 числа m=0 и M=1.

Предел числовой последовательности.

Пусть номер n неограниченно увеличивается, т.е. стремится к бесконечности ( При этом соответствующие значения последовательности приближаются к некоторому числу a. Число a называется пределом последовательности и записывается или .

Число a называется пределом последовательности , если для любого сколь угодно малого положительного числа найдется такое натуральное число N, что при всех n > N выполняется неравенство , т.е. расстояние от N до a будут меньше .

Если последовательность имеет конечный предел, то она называется сходящейся.

Пример: предел последовательности стремится к 0, т.е. последовательность сходящаяся.

Если последовательность предела не имеет (либо предел равен ), то она называется расходящейся.

Пример: последовательность не имеет предела, т.е. она расходящаяся.

Бесконечно малые и бесконечно большие величины

Если , то называется бесконечно малой величиной.

Если , то называется бесконечно большой величиной.

Основные теоремы о пределах последовательностей

Лемма 1. Алгебраическая сумма любого (но ограниченного) числа бесконечно малых величин есть также величина бесконечно малая.

Лемма 2. Произведение ограниченной переменной величины на бесконечно малую величину есть величина бесконечно малая.

Теорема 1. Предел постоянной величины равен самой постоянной,

т.е. если , то .

Теорема 2. Если последовательности и имеют пределы a и b,

то их сумма (или разность) также имеет предел, т.е.

если b, то .

Теорема 3. Если последовательности и имеют пределы a и b, то их произведение также имеет предел, т.е. если b,

то .

Следствие 1. Постоянный множитель можно выносить за знак предела

,

Следствие 2.

Теорема 4. Если последовательности и имеют пределы a и b,

то их произведение также имеет предел, т.е. если b,

то .

Теорема 5. Если , причем и

k – некоторое натуральное число, то

Теорема 6. Если , то . Обратное утверждение неверно.

Если , то при вычислении несложных пределов от дроби, в числителе и знаменателе которой стоят по одному многочлену, можно пользоваться следующим правилом:

а) если старшая степень числителя меньше старшей степени знаменателя, то предел равен 0;

пример: = 0

б) если старшая степень числителя больше старшей степени знаменателя, то предел равен ;

пример: =

в) старшая степень числителя равна старшей степени знаменателя, тот предел равен отношению коэффициентов при старших степенях.

пример: =

Предел функции

Если при функция f(x) стремится к числу А, то число А называется пределом функции в точке а.

Пример:

Основные свойства пределов функции

1. Предел алгебраической двух функций, имеющих пределы при 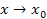равен алгебраической сумме пределов этих функций,

т.е.

2. Предел произведения двух функций, имеющих пределы при равен произведению пределов этих функций,

т.е.

3. Предел частного двух функций, имеющих пределы при равен частного пределов этих функций,

т.е.

Первый и второй замечательный предел

Первый замечательный предел

Функция в точке x=0определена, тем не менее,

ее предел при существует, причем = 1

Второй замечательный предел

Выражение , где n - натуральное число, стремится к определенному пределу, когда число . Этот предел больше 2 и меньше 3.

Следствие

Бесконечно малые и бесконечно большие функции

Функция f(x) называется бесконечно малой функцией при ,

если

Функция f(x) называется бесконечно большой функцией при , если

Две бесконечно малые функции f(x) и g(x) эквивалентными (или равносильными) при , если

Таким образом, при вычислении пределов бесконечно малые при функции можно заменять эквивалентными.

Понятие непрерывности функции

Функция называется непрерывной в точке х=х₀ , если:

1. Она определена в точке х=х_0, т.е. существует ее значение в этой точке, равное f(x);

2. Существует конечный предел функции в точке х=х₀, т.е.

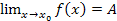
3. Этот предел равен значению функции при х=х₀, т.е.

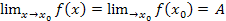
Функция непрерывна на промежутке, если она непрерывна во всех точках этого промежутка.

Геометрически непрерывность функции точке означает, что ее график не разрывается в точке, т.е. состоит из непрерывной (сплошной) линии.