Лазерная технология наряду с информационными и нанотехнологиями уверенно выдвинулась в число наиболее перспективных высоких технологий — технологий 21 века. На своем начальном этапе развития в 70-е, 80-е годы это направление науки и техники вполне обоснованно связывалось лишь с технологией сварки, резки и закалки металлов и сплавов. Лазерный отжиг полупроводников, получение новых сплавов, покрытий, аморфизация, напыление тонких пленок, модификация свойств поверхности, лазерно-плазменная технология, стереолитография, лазерная химия и т.д. еще двадцать лет назад были неизвестны. Сейчас каждый из этих процессов представляет собой самостоятельную, динамичную область исследовательской деятельности, перешагнувшей из стадии первоначальных лабораторных экспериментов в стадию новой, лазерной промышленной технологии.

С созданием мощных непрерывных и импульсно-периодических газовых и твердотельных лазеров возник целый ряд вопросов, связанных с более широким использованием этих лазеров в различных областях производства, включая и традиционные методы термического воздействия, направленные на изменение геометрии деталей (сварка, резка) и их физико-химического состояния (термоупрочнение, легирование и т.д.). Высокая интенсивность лазерных источников способствует селективному развитию. Вместе с тем, физические процессы, происходящие при воздействии коротких и ультракоротких лазерных импульсов с металлами и полупроводниковыми материалами, определяющие возможности таких быстро развивающихся областей лазерной технологии, как лазерный отжиг полупроводников, лазерное легирование, геттерирование, напыление тонких эпитаксиальных пленок, а также достижения в области лазерной химии, пока недостаточно полно отражены в монографиях и учебных пособиях. Электронная промышленность остается наиболее крупным потребителем лазерных технологических установок до настоящего времени и оказывает стимулирующее действие на развитие и совершенствование производства лазерного технологического оборудования. Применение лазеров в электронике позволило довести уровень автоматизации процессов до 85 %, обеспечив выполнение практически всех основных и вспомогательных операций. Среди таких процессов следует выделить отжиг полупроводников после ионной имплантации, легирование, осаждение и травление тонких пленок, получение окисных изолирующих слоев, геттерирование и очистку полупроводниковых пластин, формирование токопроводящих слоев и омических контактов. Кроме того, использование лазерного излучения позволяет модифицировать свойства полупроводниковых приборов, создавать структуры монокристаллического кремния на диэлектрических подложках и т.д. Применение эксимерных лазеров в качестве источника ультрафиолетового излучения в фотолитографии при нанесении изображения на фоторезист через шаблон и при прямой записи обеспечивает разрешение 90 нм, что соответствует требованиям промышленного выпуска СБИС. Обеспечивая локальность и быстроту обработки, лазерная технология приводит к ускорению перечисленных технологических процессов, снижению количества критических операций и, в конечном итоге, к повышению качества продукции по сравнению с традиционными способами. Использование коротких и мощных импульсов лазерного излучения для модификации свойств металлических материалов чрезвычайно перспективно вследствие реализации аномально высоких скоростей нагрева и остывания поверхности материала, поглотившего излучение. Это определяет широкие возможности в создании новых, уникальных по физико-химическим свойствам, структурных и фазовых состояний в металлах и сплавах, являющихся интересными объектами исследований и практических применений. Этими вопросами занимается лазерно-плазменная технология и технология получения металлических стекол. В новую современную область взаимодействия излучения с веществом вылилась лазерная химия, использующая уникальную возможность резонансного возбуждения атомов и молекул за счет высокой монохроматичности лазерного излучения. Здесь наибольший интерес представляют такие важнейшие процессы, как лазерное разделение изотопов, лазерный синтез материалов с заданными свойствами и получение особо чистых веществ.

В большинстве технологических процессов обработки материалов (исключая лазерную химию) интенсивность облучения и ее пространственно-временные характеристики играют определяющую роль, в то время как такие фундаментальные свойства лазерного излучения, как когерентность и монохроматичность не проявляют себя. Воздействие лазерного излучения сопровождается процессами тепло-и массопереноса, развитие которых зависит от энергетических и пространственно-временных характеристик излучения. В процессах лазерной технологии длина волны излучения играет существенную роль. Дело не только в дисперсии поглощения окружающей атмосферы, но и в дисперсии поглощающей способности обрабатываемых тел. Кроме того, пороги пробоя атмосферы вблизи поверхности тел могут различаться на два порядка для излучения с длиной волны 0,69, 1,06 мкм и для излучения СО2-лазеров (10,6 мкм). Зависит от длины волны излучения и глубина проникновения лазерного излучения в объем конденсированной среды, что существенно, например, при обработке пленок. При воздействии сфокусированного мощного лазерного излучения на поверхность твердого тела вещество нагревается, плавится, частично испаряется и ионизируется. В неоднородно–нагретом веществе возникает сложное течение жидкости, паров, плазмы и окружающего газа. Перемещение вещества оказывает, в свою очередь, существенное влияние на распространение лазерного излучения, приводя к изменению фокусировки и условий поглощения и отражения излучения. Возникает сложное многофазное гидро- и газодинамическое течение, согласованное с распространением лазерного излучения в сильно поглощающей и преломляющей оптически нелинейной среде. Соответствующий выбор длины волны излучения, интенсивности, времени воздействия, вида и давления окружающей атмосферы позволяет осуществлять различные технологические процессы, ряд которых принципиально невозможен без применения лазера.

Классификация лазерных технологических процессов

При анализе процессов воздействия лазерного излучения на материалы часто используют понятие «критической интенсивности» или «критической плотности потока». Этот термин в определенной степени условен, так как связан с понятием разрушения вещества, также имеющим условный характер. В лазерной обработке под началом разрушения чаще всего подразумевают плавление поверхности тела, хотя необратимые изменения в объеме большинства материалов происходят и при нагреве ниже температуры плавления. Критические интенсивности [Вт/см2] (i = 1, 2, 3, 4) являются основой, используя которую, можно классифицировать разнообразные технологические процессы и рассматривать их последовательно при переходе от одной критической интенсивности к другой. Отметим, что такой подход к анализу процессов лазерной технологии не является единственным. Обычно принимают, что:

— критическая интенсивность, необходимая для достижения к концу импульса излучения на поверхности тела температуры плавления;

— критическая интенсивность, соответствующая достижению температуры кипения;

— критическая интенсивность, выше которой процессы испарения преобладают над переносом тепла в конденсированную среду;

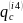— критическая интенсивность, выше которой над поверхностью возникает плазменный факел, а вглубь материала распространяется ударная волна.

Возможно использование и других условий критической интенсивности, например, для реализации глубинного проплавления и т.д. Для металлов величина лежит в диапазоне 10⁴÷10⁵ Вт/см² при длительности импульса лазерного излучения ∼ 1 мс. На этом уровне интенсивности лазерного излучения можно осуществлять термическую обработку большинства металлов. На рис. 1 предложена общая схема импульсных лазерных процессов. В определенной степени эта схема пригодна и для технологических процессов с воздействием непрерывного излучения, если под временем воздействия подразумевать не длительность импульса, а время прохождения через данную точку луча, определяемое скоростью движения луча. Рассмотрим схему подробнее. При нагреве ниже температуры плавления возможна закалка и термоупрочнение сталей и сплавов, а также геттерирование и отжиг дефектов в ионно-имплантированных слоях полупроводников. Плавление тонкого поверхностного слоя открывает возможности для получения покрытий, поверхностной очистки при плавлении, создания на поверхности металлических стекол и проведения химико-термических процессов, приводящих к созданию новых веществ. Если плотность мощности превышает , то в газовой среде вблизи поверхности тел возможна реализация процессов лазерно-плазменной обработки (разложение веществ, синтез соединений, упрочнение материалов, окисление, восстановление).

Рис. 1. Классификация лазерных технологических процессов по плотности мощности

При q > 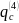∼ 10⁹ Вт/см² и длительности импульса в десятки наносекунд возможно упрочнение поверхностного слоя толщиной в единицы и доли микрометров под действием ударной волны, обусловленное генерацией структурных дефектов (дислокаций, смещенных атомов и т.д.).

Технологические процессы лазерной обработки материалов.

Технологические процессы лазерной обработки материалов:

• Отжиг (устранение повреждений в полупроводниках, вызванных имплантацией ионов при производстве интегральных схем)

• Легирование (значительное преимущество — неравновесный характер термодинамики плавления при нагреве лазерным импульсом. Резкий рост пределов растворимости примесей Sb, B, P, Ga, As в кремнии, создание тонких линейчатых структур).

• Геттерирование (Использование лазерного излучения для создания на обратной стороне полупроводниковых пластин дефектов, способных собирать загрязнения)

• Образование силицидов (электрические контакты и токопроводящие дорожки на кремниевых полупроводниках создаются силицидами металлов, после осаждения тонкого слоя металла на кремниевую подложку система «металл-кремний» нагревается лазерным импульсом до температуры прохождения химической реакции без нагрева соседних структур).

• Окисление (импульсный лазерный нагрев поверхности полупроводниковых пластин в атмосфере кислорода или на воздухе приводит к селективному окислению поверхности по заданному рисунку).

• Травление (удаление части материала (тонкой пленки) с помощью испарения лазерным лучом по заданному рисунку или обработка поверхности светом (УФ-диапазон) с изменением физических свойств и последующим химическим травлением (фотолитография)).

• Очистка поверхности (термическая десорбция поверхностных загрязнений при плавлении поверхности полупроводника лазерным лучом (аналог метода зонной очистки)).

• Осаждение тонких пленок (использование лазерного излучения как источника нагрева мишени приводит к высокой степени ионизации вещества (при q ≥ ), высоким скоростям осаждения и роста пленок, возможности сохранения сложного стехиометрического cocтава многокомпонентных соединений, улучшение свойств структуры, снижение концентрации дефектов за счет импульсной перекристаллизации).

• Скрайбирование (надрезание полупроводниковых пластин лазерным лучом с последующим механическим разломом позволяет эффективно разделять готовые структуры на отдельные микросхемы).

• Подгонка (использование лазерного луча для подгонки отдельных элементов микросхем (конденсаторов, сопротивлений) по контрольным параметрам).

В лазерной технологии металлических материалов также можно выделить ряд высокоэффективных процессов.

• Упрочнение (структура упрочненного слоя, возникающая в результате действия лазерного излучения, характеризуется высокой дисперсностью, аномально большой твердостью, пониженной химической активностью, что оказывает существенное влияние на эксплуатационные характеристики упрочненных материалов – износостойкость, фрикционные свойства, механические характеристики, теплостойкость, величину и характер распределения остаточных напряжений).

• Сварка (использование установок относительно невысокой мощности дает возможность осуществлять высококачественную скоростную точечную сварку, дающую существенные экономические преимущества).

• Пайка (лазерная пайка обеспечивает такое преимущество, как легкий контроль времени нагрева материала и дозировки энергии лазерного излучения).

• Легирование (высокие скорости нагревания и охлаждения облучаемого материала позволяют получить новые фазовые и структурные состояния, которые невозможно реализовать с помощью других нелазерных способов обработки).

• Оплавление поверхностного слоя (нанесение на поверхность детали тонкого слоя отличающегося по свойствам металла (или материала) и последующее воздействие на него лазерным импульсом (плакирование) позволяет создать на поверхности защитное покрытие).

• Получение металлических стекол (высокая скорость охлаждения (dT/dt ≥ 10⁹ К/с) расплава на поверхности может привести к аморфизации поверхности металла и образованию металлического стекла).

• Получение отверстий (применение импульсных твердотельных лазеров позволило на новом уровне решить проблему формирования (сверления) отверстий малого диаметра в таких труднообрабатываемых материалах, как рубин, корунд, алмаз, твердые керамические сплавы и т.д.)

• Лазерная обработка пленок (для снижения термического искажения рисунка подложки при обработке пленок обычно используют короткие (∼ 10 нс) лазерные импульсы).

• Термохимическая обработка (под такой обработкой понимают совокупность разнообразных процессов (разложение, окисление, восстановление, синтез), протекающих на поверхности вещества при обработке в газовой среде).

• Лазерно-плазменная обработка (при плотности потока лазерного излучения, превышающего критическое значение , над поверхностью материала образуется эрозионный плазменный факел).

Основные характеристики лазерного излучения Лазерное излучение характеризуется рядом уникальных свойств. К их числу относятся большая интенсивность (плотность потока) электромагнитной энергии, высокая монохроматичность, значительная степень временной и пространственной когерентности, возможность широкого варьирования длительности воздействия — от непрерывного излучения до импульсов длительностью в несколько фемтасекунд. Монохроматичность лазерного излучения означает узкий диапазон частот его составляющих, или малую ширину его спектра, ∆λ. Для некоторой интегральной линии с длиной волны λ₀ (частотой ν₀) степень монохроматичности µ = ∆λ/λ₀ = ∆ν/ν₀. (1) Например, для газовых лазеров, работающих в одномодовом режиме, ∆λ = 10⁻¹⁰ мкм и µ = 10⁻¹⁰. В то же время, для спектральных линий, выделенных монохроматорами, µ ≥ 10⁻⁶. Поскольку значительная часть потока излучения приходится на очень узкий участок спектра и не превосходит сотых долей микрометра, то спектральная плотность потока лазерного излучения на много порядков превосходит спектральную плотность потока излучения других известных источников электромагнитной энергии. Монохроматичность тесно связана с одним из основных свойств лазерного излучения — его когерентностью. Когерентность определяется корреляцией характеристик поля излучения, образованного в одно и то же время разнесенными в пространстве источниками (пространственная когерентность), или одним и тем же источником, но в разные моменты времени (временная когерентность). Если в результате сложения полей источников результирующая интенсивность электромагнитного излучения I в точке Q в зависимости от разности фаз может принимать значения от (√I1−√I2)² до (√I1 + √I2)², то источники когерентны. Источники полностью когерентны, если I = I1 + I2. Полезным параметром является длина когерентности l_kog, связанная с временем когерентности τ_kog соотношением

l_kog = c · τ_kog, (2)

где c — скорость света. Эта длина является приблизительной оценкой разности пути между двумя плечами интерферометра Майкельсона, при которой еще проявляется интерференция. Другими словами, если разделить луч света на два отдельных луча, проходящих различные пути, то l_kog является максимальной разностью этих путей, при которой оба луча при их соединении могут интерферировать. Время когерентности определяет отрезок времени, в течение которого разность фаз колебаний источников не успевает измениться на величину того же порядка, что и π. Время когерентности связано с шириной спектра излучения τ_kog ≈ 1/∆ν для непрерывных лазеров и для лазеров с большими длительностями импульсов τ_ι>>1/∆ν и определяется длительностью импульса τ_kog ≈ τ_ι для лазеров, работающих в режиме модулированной добротности. Так, для стабилизированного по частоте He-Ne– лазера с ∆ν = 1 МГц τ_kog = 10⁻⁶ с и l_kog = 3·10⁴ см; для многомодового He-Ne– лазера с ∆ν = 1,5 ГГц τ_kog = 6,6·10⁻¹⁰ с и l_kog = 20 см; для АИГ:Nd– лазера с модулированной добротностью и длительностью импульса 10 нс τ_kog = 10⁻⁸ с и l_kog = 300 см. Пространственная когерентность зависит от числа поперечных мод лазера. Лазер непрерывного действия, работающий на одной поперечной моде, обладает почти идеальной пространственной когерентностью. Импульсный лазер в многомодовом режиме имеетограниченную пространственную когерентность. Пространственная когерентность обусловливает высокую направленность излучения и возможность фокусирования его на площадки малых размеров, что важно при технологических процессах обработки материалов. Высокая степень временной когерентности излучения позволяет использовать лазер для осуществления процессов, связанных с интерференцией, измерением длины, линейных и угловых скоростей, малых перемещений, для передачи информации и т.д. Направленность излучения характеризуют телесным углом, охватывающим основную часть излучаемой энергии. Если телесный угол представляет собой конус, то в качестве параметра направленности излучения выбирают плоский угол расхождения потока — угол расходимости. Для телесного угла, отличающегося от конуса, обычно приводят значения двух плоских углов в вертикальной и горизонтальной плоскостях. Если полагать, что распределение амплитуды и фазы колебаний однородно в поперечном сечении потока, то его расходимость, ограниченная дифракцией, составит угол θ = 1,22λ/2r₀ (3) по уровню на половине амплитуды мощности, где 2r₀ — диаметр потока излучения. Например, для рубинового лазера λ = 0,69 мкм и при 2r₀ = 1 см θ ≈ 0, 85·10⁻⁴ рад, а для газового CO₂ лазера при том же диаметре потока и λ = 10, 6 мкм, θ ≈ 1,21·10⁻³ рад. В действительности расходимость лазерного излучения значительно выше дифракционного предела (3). Это вызвано неоднородностью распределения амплитуды и фазы поля излучения в пределах излучающей поверхности, многомодовым характером генерации излучения (точнее — колебаниями поперечных типов), наличием неоднородностей в активной среде и несовершенством элементов резонатора. Например, в твердотельных лазерах излучающая поверхность активного элемента не является однородной, а представляет собой сложную структуру в виде отдельных светящихся пятен, размер которых достигает ∼ 100 мкм, а размер образуемых ими комплексов ∼ 800 мкм. Наиболее однородным распределением интенсивности по сечению потока обладают эксимерные лазеры. Уменьшения расходимости излучения можно добиться прежде всего селекцией колебаний высших поперечных типов. Наименьший угол расходимости имеют одномодовые лазеры, генерирующие основной тип колебаний TEM00. Получение одномодового режима для твердотельных лазеров — более сложная задача, поскольку их активная среда обладает большим усилением и достаточно трудно создать значительные потери для колебаний высших поперечных типов, не ухудшая энергетических характеристик потока излучения. Поляризация — важный параметр лазерного излучения. Вид активного вещества определяет тип поляризации излучения. Например, для рубина, когда оптическая ось параллельна оси резонатора (кристалл с нулевой ориентацией), все плоскости поляризации равноценны, и излучение лазера характеризуется естественной поляризацией. Если оптическая ось кристалла и ось резонатора перпендикулярны, то излучение поляризовано в плоскости, перпендикулярной к оптической оси кристалла. В большинстве случаев лазерное излучение оказывается плоскополяризованным. Длина волны излучения также является важным параметром лазерного излучения, во многом определяющим эффективность взаимодействия с поверхностью материала, что является важнейшим условием выполнения того или иного технологического процесса. Лазерное излучение перекрывает диапазон длин волн 10⁻⁵ ÷ 10⁻² см (от ближней ультрафиолетовой до инфракрасной области, включая видимую). Используемые в технологии лазеры генерируют излучение с длиной волны λ = 0, 193 ÷ 10, 6 мкм: эксимерный ArF (ультрафиолетовый) — λ = 0,193 мкм; эксимерный KrF (ультрафиолетовый) — λ = 0,248 мкм; эксимерный KrCl (ультрафиолетовый) — λ = 0,308 мкм; азотный (ультрафиолетовый) — λ = 0,337 мкм; на красителях — λ = 0,34 ÷ 1,175 мкм; на парах меди — λ = 0,35 мкм; волоконно-оптический с ионами Yb — λ = 1,070 мкм; аргоновый Ar+ — λ = 0,49 и 0,51 мкм; полупроводниковый на GaAs — λ = 0,85 ÷ 0,9 мкм; на иттрий-алюминиевом гранате с неодимом (АИГ:Nd)-излучение с λ = 1,06 мкм; на стекле с неодимом (АИГ:Nd) — излучение с λ = 1,06 мкм; на CO₂ — излучение с λ = 10,6 мкм.

Оптические свойства металлов Оптические свойства металлов обычно описываются в терминах комплексного показателя преломления m = n − ik, (4) где n — показатель преломления, k — коэффициент экстинкции. Коэффициент экстинкции связан с коэффициентом поглощения зависимостью α = 4πk/λ, (5) где λ- длина волны. В случае нормального падения луча коэффициент отражения R0 и поглощающая способность A0 = 1 − R₀, называемая также степенью черноты поверхности є = A₀, определяются следующими выражениями: R₀ = [(n − 1)² + k²]/[(n + 1)² + k²], (6) є = 4n/[(n + 1)² + k²]. (7) Для металлов n и k являются функциями длины волны и температуры. Пример зависимости оптических коэффициентов от длины волны для титана при T = 300 K приведен на рис. 2.

Рис. 2. Зависимость оптических коэффициентов титана от длины волны при комнатной температуре

Полезно отметить, что в дальней инфракрасной области зависимость степени черноты от длины волны хорошо описывается законом є ∼ 1/λ^1/2. Параметры степени черноты є для разных металлов и разных длин волн излучения лазеров при комнатной температуре сведены в табл. 1.

Таблица 1.

Температурные зависимости степени черноты є для длин волн λ = 1,06 и 10,6 мкм представлены на рис. 3 и 4 соответственно. На степень черноты существенным образом оказывает влияние окисление поверхности металла при нагреве в атмосфере. Так, например, нагрев поверхности при 700° C в течение 2–5 мин. увеличивает степень черноты тантала почти в 10 раз.

Рис. 3. Зависимости степени черноты разных металлов от температуры для λ = 1,06 мкм

Рис. 4. Зависимости степени черноты разных металлов от температуры для λ = 10,6 мкм

Роль степени черноты наиболее важна лишь на начальной стадии взаимодействия лазерного излучения с поверхностью металла. В процессе нагрева и особенно после начала разрушения поверхности степень черноты значительно возрастает, что значительно увеличивает эффективность передачи энергии от лазерного излучения металлам. Учитывая высокую степень поляризации лазерного излучения при обработке материалов наклонным пучком важно учитывать зависимость коэффициента отражения от угла падения луча, представленную на рис. 5.

Рис. 5. Обобщенная диаграмма зависимости коэффициента отражения поверхности разных металлов от плотности энергии

Процессы нагрева материалов при воздействии лазерного излучения

При воздействии лазерного излучения на поверхность металла, начиная с момента времени t > τ_ep ≈10⁻¹¹ ÷ 10⁻¹² с, происходит выравнивание температур электронного газа и решетки, что позволяет использовать понятие “источника тепла” для описания теплового воздействия лазерного излучения. Поскольку значительная часть технологических процессов выполняется при умеренных плотностях потока q ≤ 10⁹ Вт/см² и длительностях импульса τ_i ≥ 10⁻⁸ с >> τ_ep, понятие “источник тепла” является вполне корректным. В соответствии с этим задачи о нагреве материалов лазерным излучением могут быть рассмотрены с использованием закономерностей обычной теплопроводности (линейной и нелинейной). Границей этого приближения можно условно считать времена ∼ 10⁻⁹ с. Тепловой источник, эквивалентный действию луча лазера, может быть поверхностным или объемным, сосредоточенным или распределенным в зависимости от поставленной задачи, выбираемой расчетной схемы и физических характеристик материала. При указанных ограничениях на плотность потока излучения можно пренебречь потерями тепла за счет лучеиспускания и конвекции с нагреваемой поверхности. В ряде случаев учет температурной зависимости теплофизических и оптических постоянных не вносит больших изменений в конечный результат, что позволяет в первом приближении рассматривать более простые задачи с не зависящими от температуры коэффициентами. Основными задачами теплофизики при лазерном нагреве материала является определение динамических характеристик температурного поля на поверхности и в глубине материала с целью получения информации о таких важнейших параметрах любого технологического процесса, как глубина прогретого фронта, критические плотности потока лазерного излучения, скорости нагрева и охлаждения поверхности, градиент температуры и др. Для нахождения значения температуры в любой точке облучаемого материала в любой момент времени необходимо найти решение T(x, t) уравнения теплопроводности, которое в общем случае для полубесконечного тела и неподвижного источника тепла имеет вид:

(8)

где ρ, c, κ– теплофизические коэффициенты (плотность, теплоемкость и теплопроводность), являющиеся в общем случае функциями температуры, пространственных координат и времени; q_v —плотность мощности объемного источника тепла.

На практике наибольший интерес представляют изотропные системы, у которых свойства одинаковы по всем направлениям, а теплофизические коэффициенты не зависят от температуры. В этом случае уравнение (8) принимает вид:

(9)

где a = κ/ρc– коэффициент температуропроводности, ∆ — оператор Лапласа. При воздействии лазерного излучения на металлы источник тепла является поверхностным, и q_v в (9) обращается в нуль. Тогда лазерное излучение как источник тепла входит в граничное условие второго рода:

(10)

где x — координата в глубину полубесконечного тела, q₀ — плотность потока лазерного излучения на поверхности. Аналитически уравнение теплопроводности решается лишь в ряде простейших случаев, которые подробно изложены в монографии Дьюли. Для точного определения T(x, t) необходимо в каждом конкретном случае находить решение численными методами на компьютере. Однако анализ аналитических решений, полученных при разумных упрощениях, позволяет выявить закономерности нагрева материалов, которые, как показывает опыт, достаточно хорошо описывают реальную картину нагрева материала.

Нелинейные случаи нагрева материала лазерным излучением

Большинство задач воздействия лазерного излучения на металлы, полупроводники и другие непрозрачные материалы следует рассматривать в нелинейной постановке. К нелинейным задачам нагрева относятся те, в которых один из перечисленных параметров зависит от температуры: а) коэффициент теплопроводности, б) коэффициент удельной теплоемкости, в) коэффициент теплоотдачи, г) тепловой поток на поверхности, д) внутренние источники (стоки тепла), е) положение границ тела.

Рис. 6. Зависимости изменения температуры от времени на алюминиевом образце, облучаемом несфокусированным лучом лазера (τ_i = 30 нс, q₀ = 20 МВт/см²), на глубинах: 1) x = 0, 2) x = 700 нм, 3) x = 2000 нм

Задачи, где от температуры зависят теплофизические коэффициенты, называют задачами с нелинейностями 1-го рода; где нелинейности вносят граничные условия — задачами с нелинейностями 2-го рода; где источники тепла зависят от температуры - задачами с нелинейностями 3-го рода. Если плотность потока излучения не превосходит первой критической плотности , наиболее важны задачи 1-го и 2-го рода. Если же плотность потока излучения превосходит , то по прошествии некоторого времени τ_m, за которое достигается температура плавления на поверхности материала, необходимо рассмотреть задачи с нелинейностями 3-го рода; т.е. с нахождением положения границы раздела фаз. При воздействии мощных потоков лазерного излучения обычно встречается наиболее общая задача, в которой все три вида нелинейностей присутствуют одновременно. В случае нагрева материала до температуры плавления наибольшее влияние на результаты решения уравнения теплопроводности оказывает зависимость оптических постоянных среды от температуры, которая достаточно хорошо описывается линейным законом: (11)

где a₀ = 0, 75V_F /c, (V_F — скорость электрона на поверхности Ферми, c — скорость света; b = Ω_pl/2πσ₀, Ω_pl = (ne2/mκ₀)^0,5 — плазменная частота, n, e, m — соответственно концентрация, заряд и масса электрона; σ₀ — статическая электропроводность, κ₀ — диэлектрическая проницаемость). Значения коэффициентов a₀ и b, взятые из опытных данных, приведены в табл. 2.

Таблица 2.

Приведенные в таблице данные соответствуют температурному диапазону до достижения точки плавления на поверхности материала. При A = A(T ) решение одномерной задачи теплопроводности (r_s >> √at) распадается на два случая — больших и малых значений параметра s = 4bq₀: (12)

(13)

где q₀ — плотность потока излучения на поверхности; T₀– начальная температура поверхности материала; A₀ = A(T₀)– начальное значение поглощающей способности среды.

Учет температурной зависимости поглощающей способности среды приводит к следующим особенностям в процессе нагрева. При s >> 1 , т.е. при очень больших плотностях потока лазерного излучения, возникает peжим нагрева, не имеющий аналога в задаче с постоянным значением поглощающей способности среды A = A₀. В этом случае температура поверхности материала экспоненциально возрастает со временем (12). В случае умеренных плотностей потока s < 1 (наиболее чаcто реализуемый случай) можно выделить два режима нагрева, определяемых временным интервалом.

Для отрезков времени t < τ = (ρc√a/bq₀)² увеличение температуры поверхности происходит в соответствии с формулой, полученной из (13) при b → 0:

(14)

Таким образом, учет зависимости A = A(T) для отрезков времени T < τ несущественен, и температура поверхности имеет корневую зависимость T ∼ √t от времени, как и в случае решения линейной задачи теплопроводности.

При t >> τ из (13) можно получить выражение:

(15)

Следовательно, начиная со времени τ1>> τ, рост температуры выходит на экспоненциальную зависимость. Учет температурной зависимости A(T) изменяет значение плотности потока, необходимой для достижения заданной температуры поверхности к концу действия лазерного импульса. Например, при облучении серебра неодимовым лазером с длиной волны 1,06 мкм для достижения на поверхности температуры плавления за τ_m= 10⁻⁸ с без учета зависимости поглощающей способности от температуры A = A₀ имеем = 3·10⁷ Вт/см², а с учетом ее: A = A(T), = 9,5·10⁶ Вт/см².

Графически решения уравнения теплопроводности в случае умеренных плотностей потока (s < 1) приведены на рис. 7:

Рис. 7. Зависимость температуры поверхности металла от времени в случае решения нелинейной и линейных задач

1)решение нелинейной задачи при A = A(T);

2) решение линейной задачи при A = A₀;

3) решение линейной задачи при среднем значении поглощающей способности A = [A₀ + A(T_m)]/2.

Из рисунка видно, что решение нелинейной задачи уравнения теплопроводности при A = A(T) лежит в пределах, полученных для линейных задач, при начальном A₀ и усредненном A = [A₀+A(T_m)]/2 значениях поглощающей способности материала. Для моментов времени, превышающих характерное значение τ₁, pocт температуры поверхности металла выходит на экспоненциальную зависимость. Решение двумерной задачи уравнения теплопроводности в нелинейном случае для острой фокусировки (r_s >> √at) приводит к существенным качественным отличиям от случая одномерной задачи: в одномерном случае температура с течением времени при b ≥ 0 безгранично возрастает, а при b < 0 стремится к постоянной величине. В пространственной постановке задачи температура всегда стремится к постоянной величине при t → ∞, причем при b > 0 температура быстрее стремится к предельному значению, чем при b < 0.

Зависимость теплофизических коэффициентов материалов от температуры (нелинейности 1-го рода) обычно учитывается при решении уравнения теплопроводности методами линеаризации. При этом коэффициент теплопроводности может как возрастать с температурой (для Cu, Fе, Au и др.), так и уменьшаться (Mo).

В результате учета нелинейностей 1-го рода характер температурной зависимости от времени в целом сохраняется, хотя значения реальных температур могут значительно отличаться от расчетных данных, полученных для постоянных значений κ, ϱ и c.

Плавление и испарение материала под действием импульсов лазерного излучения Ранее мы рассмотрели нагрев материала, поглощающего лазерное излучение, в отсутствие поверхностного плавления. Теперь обсудим режим взаимодействия, при котором в облучаемом материале происходит фазовый переход. Необходимо отметить, что строгое математическое описание процесса плавления при таком взаимодействии, учитывающем многообразие физических процессов, является весьма сложным, и в каждом конкретном случае задача решается численными методами. Вместе с тем, поскольку многие приложения лазеров к обработке материалов связаны с началом фазовых превращений, полезно проводить оценку прохождения того или иного технологического процесса на основе упрощенного модельного представления. К примеру, лазерное сверление включает нагрев до испарения, но присутствие жидкой фазы играет существенную роль. Рассмотрим результаты некоторых моделей лазерного сверления. Модель плавления-вымывания. При достижении температуры плавления образуется область расплава. В отсутствие возмущений граница расплава будет распространяться вглубь вещества со скоростью:

(16)

где L_m — скрытая теплота плавления, ∆ — толщина расплава. При v_m∆/a << 1, получаем, что 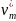= Aq₀/(ρL_m + ρcT_m) — максимальная скорость движения расплава. Зависимость толщины расплава ∆ от времени находится из уравнения сохранения объема вещества:

(17)

где dVp/dt — потери расплава в единицу времени, вызванные внешними причинами, например, потоком газа, S– площадь зоны расплава. Если расплав непрерывно удаляется, то скорость фронта плавления и ∆(t) = t. Если расплав не удаляется, то его температура растет и достигает температуры кипения T_b. Это сопровождается возникновением волны испарения, движущейся со скоростью

(18)

где L_b — скрытая теплота испарения. При достижении третьей критической плотности мощности возникает эффект выдавливания жидкой фазы давлением паров и скорость сверления возрастает от значения v_b до значения (рис. 8)

.

Рис. 8. Зависимость скорости сверления от плотности мощности в модели плавление-вымывание

Как отмечалось выше, с ростом плотности потока лазерного излучения материал нагревается до все более высоких температур. Экспериментальные исследования показывают, что при заданной форме и длительности лазерного импульса существует достаточно четко определенная критическая плотность потока излучения – , зависящая от теплофизических характеристик облучаемого вещества, начиная с которой происходит интенсивное испарение вещества, при больших плотностях потока излучения скорость движения фронта испарения не определяется кинетикой фазового перехода, а зависит в основном от скорости подвода энергии к облучаемому веществу. Образующийся при этом пар сильно экранирует облучаемую поверхность, так что главная часть энергии излучения превращается во внутреннюю и кинетическую энергию образующейся и расширяющейся плазмы, и эффективная удельная энергия испарения оказывается значительно выше, чем обычная теплота испарения. Поскольку скорость испарения облучаемого материала сильно зависит от температуры, существует резкая нижняя граница плотности потока излучения , соответствующая началу испарения. При q < эффективная удельная энергия разрушения материала велика. С ростом плотности потока излучения она уменьшается и при некотором значении c достигает своего наименьшего значения. Таким образом, при q = устанавливается стационарный режим испарения, т.е. стационарное движение между твердой и газообразной фазами. Внутри промежутка < q < образуется переходный режим, при котором происходит нагревание поверхности облучаемого материала от комнатной температуры до температуры, при которой происходит испарение и, соответственно, увеличивается скорость фазовой границы. Естественно, что переходный процесс сопровождается перераспределением поглощенной энергии. При неподвижной границе вся поглощенная энергия отводится внутрь материала за счет теплопроводности, а при стационарном движении границы фаз роль теплопроводности становится несущественной, основная часть поглощенной энергии идет на испарение материала. Характеристики процесса испарения облучаемого материала в области действия теплового механизма < q < можно получить, решая одномерную задачу теплопроводности, в которой предполагается, что поглощающий слой бесконечно тонкий. Задача ставится следующим образом: на поверхности материала x = 0, занимающего полупространство x > 0, поглощается тепловой ток плотностью q (Вт/см²), и, как следствие этого, поверхность стационарно перемещается вглубь материала со скоростью V_b; тепловой поток (плотность потока излучения) постоянен. В системе координат, связанной с движущейся границей фаз, задача теплопроводности запишется в виде

(19) где x₀ = x − V_bt, ∆H — разность удельных энтальпий твердой и газообразной фаз. В предположении стационарности процесса в движущейся системе координат и независимости теплопроводности и теплоемкости материала от температуры решение задачи представится в виде

(20)

Для одноатомного газа (c = 3/2k_B) без учета скачка температуры на фронте испарения легко получить выражение для разности энтальпий в виде ∆H = L_b−RT/2µ, где k_b — постоянная Больцмана, L_b — скрытая теплота испарения, R — универсальная газовая постоянная, µ — молекулярный вес. Решение (20) не дает в явном виде скорость движения фазовой границы, а только устанавливает связь этой скорости и температуры поверхности металла T₀. Объединяя выражение (20) и выражение для ∆H, получим:

(21)

При малых плотностях потока излучения первое слагаемое, стоящее в знаменателе (21), является основным (т.е. нет зависимости V_b от кинетики испарения). Однако с ростом q скорость движения фазовой границы становится все более зависящей от температуры испаряющей поверхности, причем рост температуры при увеличении q будет продолжаться до тех пор, пока внутренняя энергия пара не достигнет теплоты испарения. Тогда движение фазовой границы будет уже зависеть от газодинамики расширения пара, появится зависимость термодинамических величин от температуры, и для корректности решения такой задачи необходимо будет учитывать поглощение излучения в паре.

Свойства лазерной плазмы

В области плотностей потока лазерного излучения q ~10⁹ Вт/см² уже возможно образование плазмы, причем образующая плазма так же, как и частицы конденсата, может поглощать и рассеивать лазерное излучение. В этом случае наиболее важную роль играют поглощение возбужденными атомами и электронами (тормозное излучение и фотопоглощение), а также поглощение частицами конденсата.

Начальная плотность частиц в образующемся газе (паре) n₀ достаточно высока, поэтому длина свободного пробега частиц гораздо меньше всех характерных геометрических размеров при расширении такого газа (пара) в вакуум или в среду. Это означает, что здесь происходит не молекулярное течение газа, а гидродинамическое, т.е. режим течения газа как целого.

Условно структуру эрозионной лазерной плазмы можно разделить на три области (рис. 9):

Рис. 9. Характерные области лазерной плазмы

I — плотное горячее ядро плазменного факела, поглощающее лазерное излучение.

II — зона ускорения, в которой тепловая энергия плазмы переходит в энергию направленного газодинамического движения.

III — область, в которой скорость частиц выходит на ассимптотическое значение, а тепловая энергия плазмы существенно меньше энергии направленного движения.

Исследования лазерной плазмы распадаются на две группы: 1) Исследование плазменного сгустка в момент образования. Здесь применяются методы оптической спектроскопии и интерферометрии. 2) Изучение бесстолкновительной лазерной плазмы на поздних стадиях разлета с помощью коллекторных и масс-спектрометрических методов. На этой стадии реализуются следующие цели: получение количественной информации о ионной и электронной составляющих лазерной плазмы; исследование энергетических и пространственных спектров ионов, идентификация массового

Фокусировка лазерного излучения

Основным параметром в большинстве приложений лазеров в обработке материалов является интенсивность лазерного луча. При прохождении лазерного луча в оптической системе его интенсивность изменяется вдоль оптической оси, увеличиваясь в областях сходимости луча и уменьшаясь в областях его расходимости. Хотя интенсивность луча изменяется, при отсутствии поглощения или других потерь его мощность остается постоянной. Изменения интенсивности связаны с изменениями пространственной ширины луча. Эти изменения возникают вследствие дифракции и фокусировки. Для предсказания эффектов лазерного излучения нужно знать пространственную ширину лазерного луча при его прохождении через оптическую систему. Например, обычно нужно знать распределение лазерной интенсивности в окрестности точки фокуса или в самой этой точке.

Р ис.2.1.

Фокусировка гауссового луча простой линзой и распределение интенсивности в трех точках вдоль оптической оси.

Простой расчет распределения интенсивности в области фокуса возможен только для луча с гауссовым профилем. Как уже упоминалось, это — профиль луча лазера, работающего на основной моде ТЕМ₀₀.

На рис. 2.1. показана фокусировка гауссового луча простой линзой и распределение интенсивности в трех точках вдоль оптической оси. Так как первоначальная расходимость луча маленькая, фокус луча расположен вблизи фокуса линзы с правой стороны(S´~f). Из теории дифракции на круглом отверстии следует , где 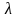— длина волны, 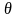´— апертурный угол, — радиус гауссова луча в его фокусе. Так как луч заполняет линзу, можно принять 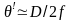, где D— диаметр линзы. Тогда

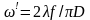
Это — радиус пятна в фокусе линзы при дифракционном пределе расходимости луча. Так как диафрагменное число f / D=F, то .

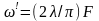Так как на практике трудно получить F<< 1, минимальный радиус пятна в условиях идеального распространения и фокусировки (ω´~λ). Таким образом, минимальный размер пятна порядка длины волны. Этот предел может достигаться в лазерах, работающих на моде ТЕМ₀₀ в видимой и инфракрасной областях. Однако для приближения к дифракционному пределу в других оптических системах необходимо свести к минимуму аберрации.

Таблица 2.1. Расчетные значения 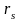, для лазеров различных типов

Тип лазера	Расходимость луча, мрад	, см
Не— Nе	0,5	10-3
Ar+,Kr+	0,5	10-3
Рубиновый	1	2·10-3
CО2	2	4·10-3
Nd — ИАГ	3	6·10-3
Неодимовый	5	10-2

Простая оценка минимального радиуса пятна при идеальной фокусировке может быть выполнена, согласно выражению

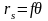(2.1)

где f— фокусное расстояние линзы, — расходимость луча. Расчетные значения , для лазеров наиболее употребительных типов приведены в таблице 2.1. Они вычислены по значениям расходимости, типичным для коммерческих лазеров, и не отражают уровня развития лазерной технологии на данном этапе.

Следующей важной характеристикой сфокусированного луча является глубина резкости при фокусировке. Она может определяться различными способами и характеризует допустимое изменение расстояния линза — изображение, при котором размеры пятна существенно не изменяются. Полезные оценки могут быть сделаны, согласно соотношению

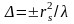(2.2)

где — радиус пятна и знаки «±» соответствуют глубине резкости при движении к линзе и от нее. При ~λ имеем Δ~λ. Отсюда следует простое правило: глубина резкости примерно равна размеру пятна. При >λ глубина резкости, конечно, значительно превышает размер пятна.

В качестве примера информации, которая может быть получена с помощью простых выкладок, рассмотрим фокусировку лазерного луча

Аг⁺-лазера мощностью 10 Вт с помощью линзы с параметрами f = 2 см, D = 1 см. Рассмотрим два варианта. В первом линза используется непосредственно для фокусировки луча. Во втором предполагается, что перед последней фокусирующей линзой помещен 10-кратный расширитель луча. Примем диаметр лазерного луча равным 1 мм, а его расходимость равной 0,5 мрад.

Простая линза. Так как диаметр линзы D значительно больше диаметра луча, для оценки размеров пятна используем выражение , где — расходимость луча. Тогда = 1,0*10^-3 см = 10 мкм. Максимальная интенсивность I₀ в фокусе луча связана с мощностью луча Р соотношением

.

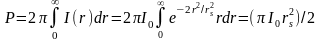(2.3)

Таким образом, 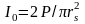=6,4 МВт/см². Расчётная глубина резкости при фокусировке Δ= ± 10^-2 см=±100 мкм.

Расширитель луча и простая линза. При расширении луча в 10 раз перед фокусирующей линзой во столько же раз уменьшается его расходимость, т. е. мрад. Отсюда = f θ = 10^-4 см и I₀ = 6,4 10⁸ Вт/см². Глубина резкости равна ± 10^-4 см.

Эта простая оценка показывает преимущества расширения луча для заполнения апертуры фокусирующей линзы. Такое расширение уменьшает расходимость луча и . Это в свою очередь увеличивает интенсивность в области фокуса. Отметим, однако, что увеличение I₀ получено только за счет соответствующего уменьшения глубины резкости. В ряде приложений на размеры пятна накладывается ограничение требованием большой глубины резкости, так что расширение луча может оказаться не столь полезным.

Хотя при данных условиях можно вычислить диаметр сфокусированного луча, из-за отсутствия безаберрационной оптики этот расчет дает только нижний предел размера пятна, которое может быть получено в данной системе. Таким образом, обычно требуются измерения диаметра луча. Существует несколько способов его измерения. Во всех требуется наличие гауссового профиля.

Особенно простой результат получен методом перемещения в луче кромки ножа. Мощность прошедшего луча равна:

(2.4)

где а = х— координата кромки ножа. Эти измерения можно осуществить на основе лазера непрерывного действия с помощью прерывателя и фотоприемника. Выход приемника можно регистрировать с помощью осциллографа и использовать длительность и форму импульсов для расчета радиуса гауссового луча ω.