1.сведения о форме и размерах земли,влияние кривизны земли на точность геодезических измерений.системы координат и счета высотБприменяемые в геодезии.

1. Сведения о форме и размерах Земли, влияние кривизны Земли на точность геодезических измерений.

Земля – сочетание возвышенностей и углублений. Углубления заполнены водой 71% океаны. Под действием силы тяжести вода образует уровенную поверхность, перпендикулярная в каждой точке направления силы тяжести. Линию совпадающую с направлением силы тяжести называют отвесной линией. Если уровенную поверхность мысленно продлить под материками, образуется фигура называемая геоидом. Из-за неравномерного распределения масс внутри Земли поверхность геоида имеет сложную форму. Поэтому за фигуру для земли принимают эллипсоид вращения. Земной эллипсоид с определенными размерами и ориентированный определенным образом для части Земли называется референц-эллипсоидом.

Параметрами, определяющими его размеры и форму, являются большая а и малая b полуоси или большая полуось а и полярное сжатие а т= (а — Ь)/а Величины этих параметров могут быть получены посредством градусных измерений, т. е. путем геодезических измерений длины дуги меридиана. Зная длину градуса в различных местах меридиана, можно установить фигуру и размеры Земли.

R_земли = 6371,11 км (при стр-ве), a = 6378 км (больш. полуось), b = 6356 км (меньш. полуось)

Сжатие Земли ∂ = 1/298,3 (∂=(a-b)/b)

Системы координат и счета высот, применяемые в геодезии.

Координаты - величины, определяющие положение точек на поверхности земли относительно определенных осей или плоскостей.

• Географическая система координат

• Зональная система координат

• Прямоугольная система координат

• система координат Гаусса-Крюгера

• Полярная система координат

• Плоская прямоугольная система координат

2.ориентирование линий.ориентирные углы и их взаимосвязь. Переход от диррекционных углов линий местности к румбам.

2.Ориентировать линию - определить ее положение относительно другого направления принятого за исходное, в качестве исходных берут следующие направления : Nи - северное направление истинного меридиана, Nn- северная меридиана, N0-северное направление осевого меридиана зоны или направления параллельного ему.

Ориентирные углы и их взаимосвязь

Дирекционный угол - угол, измеряемый от северного направления осевого меридиана и заданным направлением измеренным по часовой стрелке.

Румб - острый угол r ,измеряемый от северного или южного осевого меридиана до заданного направления в ближайшую сторону.

r_СВ = α_OA

r_ЮВ = 180 - α_ON

r_ЮЗ = α_OK - 180

r_СЗ = 360 - α_OM

3.топографические карты и планы ,их масштабы и точность. Условные знаки на топографических картах и планах. Рельеф местности и его изображение на топографических картах и планах.

3. 1.Карта - уменьшенное, построенное в картографической проекции, обобщенное изображение земли

План - уменьшенное подобное изображение на плоскости горизонтального проложения участка поверхности

На плане, в отличии от карты, изображения получают практически без искажения

Масштаб - отношение длины линии на плане к горизонтальному проложению соответствующей линии на местности

Точность масштаба - горизонтальное проложение линии местности, соответствующее 0,1 мм на плане или карте данного масштаба

Масштабы: численные; именнованые; графические (линейные и поперечные)

Линейн масшт- это мерн линейка на план/карте, при помощ кот можн, не прибег к вычисл, измер любую линейн величин

Числ масшт- масштаб, выраж числ, в кот числит - 1, а знамен - число, показ, во скольк раз уменьш линейн разм карт/плана

Попер масшт- граф масшт в виде номограммы, построение кот основано на пропорц отрезков || прям, пересек стороны угла

Масштабы 1:50000, 1:25000, 1:10000 относятся к топографическим картам; масштабы 1:5000, 1:2000, 1:1000, 1:500 относятся к топографическим планам

3.2.Масштабные условные знаки- объекты, размеры которых можно нанести на план или карту в создаваемом масштабе. (длина дороги, площадь леса...)

Внемасштабные условные знаки- объекты, размеры которых нельзя нанести на или карту в создаваемом масштабе, но их наличие обязательно. (дерево, мельница... )

Пояснительные условные знаки- знаки, которые дают дополнительные характеристики объектов местности: собственные названия объектов, их назначение, количественные и качественные характеристики. ( Мост длина-ширина/грузоподъемность ; Сосна средняя высота дерева/толщина ствола расстояние рядом)

3.3.Формы и изображение рельефа

Рельеф - совокупность неровностей Земной поверхности. На картах и планах изображается горизонталями в сочетании с подписью отметок характерных точек.

Основные формы рельефа:

Гора

Впадина

Хребет

Лощина

Седловина

Горизонталь - линия, соединяющая точки Земной поверхности с одинаковыми высотами

На картах и планах высоты горизонтали изменяются через равные промежутки; разность 2х высот соседних горизонталей называется высотой сечения, а расстояние между горизонталями по к-л направлению - заложением

При высоте сечения 1,5,10 и 20 утолщают каждую 5 горизонталь с отметками. При 2,5 утолщают каждую 4 горизонталь кратную 10 м.

Бергштрихами показывается направление ската (идет от вершины)

Для характеристики крутизны ската (- степень понижения или повышения высот местности) используют угол наклона (- угол, образованный линией местности и горизонтальной плоскостью) и уклон линии местности (- отношение превышения к горизонтальному проложению)

4.решение прямой и обраьной геодезических задач.связь между дирекционными углами смежных линий.

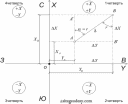
4.1.При решении прямой геодезической задачи по известным координатам одной точки, дирекционному углу линии и расстоянию между 2мя точками находят координаты 2ой точки

Xb=Xa+d*cos∂_AB ; Yb=Ya+d*sin∂_AB

Решение обратной геодезической задачи

При решении обратной геодезической задачи, по известным координатам 2х точек находят расстояние между этими точками и дирекционный угол линии, соединяющей эти точки

∆X=Xa-Xb ; ∆Y=Ya-Yb ; d=√(∆X²+∆Y²) ; cos∂=∆X/d ; sin∂=∆Y/d