C) Расчет нормального статистического распределения и вероятности
Для нахождения нормального статистического распределения используется функция «НОРМ.СТ.РАСПР», имеющая вид в конструкторе функций: НОРМ.СТ.РАСП. (число;логическое_значение).
Начнем с построение двух новых столбцов: Fi и Fi+1. Рассмотренную формулу применяем для каждого из них, используя как «число» соответствующий показатель в столбце Zi для Fi и в Zi+1 для Fi+1. В «логическое_значение» ставим 1 для того, чтобы функция нашла стандартное нормальное интегральное распределение.
Вероятность находим как разницу между нормальным статистическим распределением: Fi и Fi+1. Таким образом получаем формулу для расчета:
Pi = (Fi+1) - Fi .
Формируем столбец mi, умножая на соответствующее значение предыдущего столбца на 100. Получаем: mi= Pi*100.
Определим
значение
=
.
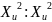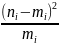По данной формуле при
помощи прямых ссылок на построенные
ранее величины находим
для
каждого значения
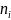соответственно.
Под
последним значением столбца находим
сумму всех показателей данного столбса
при помощи функции «СУММ», вводя в нее
в качестве аргумента все значения в
обрабатываемом столбце.
Следующим шагом необходимо расчитать критическое значение , используя функцию «ХИ2.ОБР.ПХ». Данная функция помогает сравнить наблюдаемые и ожидаемые результаты и определить, верна ли поставленная гипотеза. В конструкторе функций она выглядит следующим образом: ХИ2.ОБР.ПХ(вероятности;степени_свободы). Вероятность равна 0,05, а число степеней свободы находится при вычетании 3 из количества интервалов. В данной работе таких интервалов 7: 7-3=4- число степеней свободы.
Исходя
из полученного неравенства:
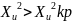делаем вывод о
том, что гипотеза не отвергается.
Zi+1 |
Fi |
Fi+1 |
mi |
Xu-2 |
|
|
|
|
|
-1,79264 |
2,9022E-27 |
0,036515 |
3,65154 |
0,033253 |
-1,14148 |
0,0365154 |
0,126836 |
9,032047 |
0,103734 |
-0,8159 |
0,12683588 |
0,20728 |
8,044409 |
1,152158 |
-0,49031 |
0,20727997 |
0,311956 |
10,46757 |
0,224345 |
-0,16473 |
0,31195567 |
0,434577 |
12,26211 |
0,044403 |
0,160847 |
0,43457681 |
0,563893 |
12,93163 |
0,000361 |
0,486428 |
0,56389314 |
0,686668 |
12,2775 |
0,874936 |
0,812009 |
0,68666818 |
0,791607 |
10,49386 |
2,889078 |
1,13759 |
0,79160677 |
0,872354 |
8,074735 |
0,000692 |
543,6666 |
0,87235412 |
1 |
12,76459 |
0,598762 |
|
|
|
Xu 2 = |
5,921721 |
|
|
|
Xu 2 kp = |
14,06714 |
Табл.3