ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВСЕРОССИЙСКАЯ АКАДЕМИЯ ВНЕШНЕЙ ТОРГОВЛИ

МИНИСТЕРСТВА ЭКОНОМИЧЕСКОГО РАЗВИТИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ»

Факультет внешнеторгового менеджмента

Дневное отделение

Кафедра мировой и национальной экономики

ПРЕДМЕТНО-АНАЛИТИЧЕСКАЯ СПРАВКА

По дисциплине «Математические методы принятия оптимальных решений» на тему «Решение производственной задачи с использованием Excel»

Работу выполнил: Студент 2 курса ФВМ ДО Еремин Данила

Научный руководитель: Кандидат физико-математических наук, старший научный сотрудник Шапошникова Г.А.

Работа сдана на кафедру Оценка работы

« » ____________ 2016г. ______________

« » _____________ 2016г.

Москва - 2016

Оглавление

Введение 3

Постановка задачи 4

Математическая модель задачи 5

Решение задачи 6

Расшифровка отчетов 9

4.1 Отчет по результатам 9

4.2 Отчет об устойчивости 10

4.3 Отчет по пределам 15

Заключение 18

Введение

Для быстрого решения классических оптимизационных задач используется надстройка «Поиск решения», входящая в программу Microsoft Excel.

Цель работы:

Цель данной работы – ознакомится на практике с инструментом «Поиск решения» Microsoft Excel, решив производственную оптимизационную задачу.

Задачи работы

• Изучить методы решения оптимизационных задач при помощи встроенного в Excel инструмента «Поиск решения».

• Решить производственную задачу

• С помощью отчетов, которые автоматически генерируются инструментом «Поиск решений», проанализировать решение.

• Углубить свои знания в математических методах принятия решений

Постановка задачи

Для строительства домов на 15 строительных площадках выбрали пять типовых домов. По каждому из проектов известны: длительность закладки фундаментов и строительства остальной части здания в днях, а также жилая площадь дома и прибыль от продажи 1 кв. м. жилой площади.

Тип Дома	1	2	3	4	5	Ресурсы времени
Фундамент	20	30	35	30	40	4500
Остальные работы	40	20	50	35	40	6000
Жилая площадь	3000	2000	5000	4000	6000
Прибыль от 1 кв. м., тыс. руб	70	80	60	65	50

Для получения максимальной прибыли при заданных ограничениях, необходимо найти и рассмотреть оптимальный план выпуска продукции. Так же необходимо решить эту же задачу при дополнительном ограничении: число домов каждого типа должно оказаться не менее, чем 10.

Математическая модель задачи

Тип Дома	Тип 1	Тип 2	Тип 3	Тип 4	Тип 5	Ресурсы времени
Фундамент	20	30	35	30	40	4500
Остальные работы	40	20	50	35	40	6000
Жилая площадь	3000	2000	5000	4000	6000
Прибыль от 1 кв. м., тыс. руб	70	80	60	65	50
Прибыль со всего дома, тыс. руб	210000	160000	300000	260000	300000
Кол-во ед. продукции

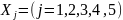– количество единиц произведенного продукта j-го типа.

Целевая функция – суммарная прибыль от реализации всей произведенной продукции:

Ограничения на количество используемых ресурсов:

Решение задачи

Чтобы найти оптимальное решение задачи, то есть найти план выпуска продукции

обеспечивающего максимальную прибыль при выполнении ограничений на ресурсы и условия неотрицательности, необходимо использовать инструмент «Поиск решений» в Microsoft Excel. В качестве исходных данных задаем нулевые значения (рисунок 1) для . Чтобы вычислить целевую функцию и количество использованных ресурсов, используем встроенную в Excel функцию «СУММПРОИЗВ».

Рисунок 1. Вносим необходимые данные, задаем нулевые значения для количества единиц продукции, используем функцию "СУММПРОИЗВ"

Далее нужно приступить к использованию инструмента «Поиск решений» (рисунок 2).

Рисунок 2. Ввод необходимых параметров

Результат работы инструмента (рисунок 3) показал, что для получения максимального дохода

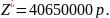
при данном количестве ресурсов, необходимо построить:

• 45 домов типа 1

• 120 домов типа 4

дома типа 2, 3, 5 строить не нужно.

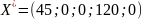
Рисунок 3 Результат