Тема 1. Обратная матрица для матриц произвольного размера и ее применения

Задания

1. Для данной матрицы определить «правую» обратную матрицу равенством: , где 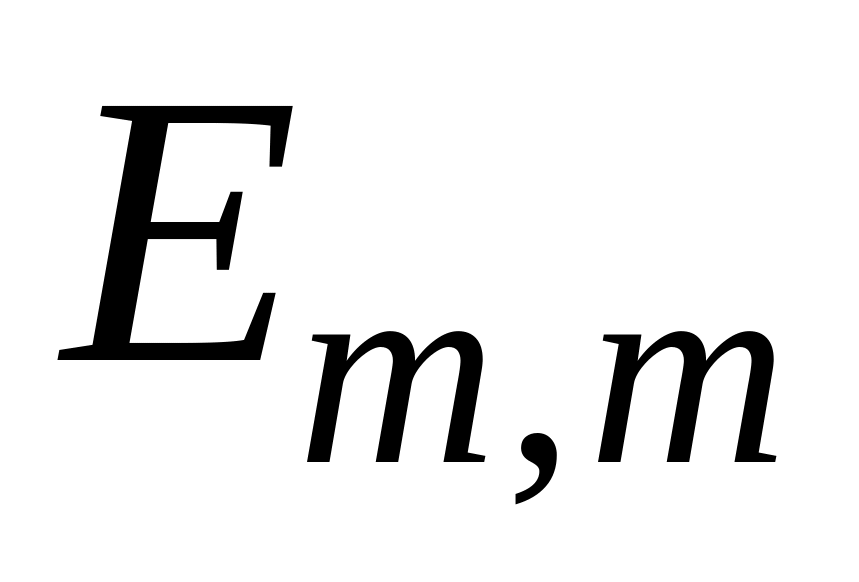– единичная матрица размера .

2. Изучить вопрос существования «правой» обратной матрицы, выяснить структуру обратной матрицы в зависимости от чисел , , .

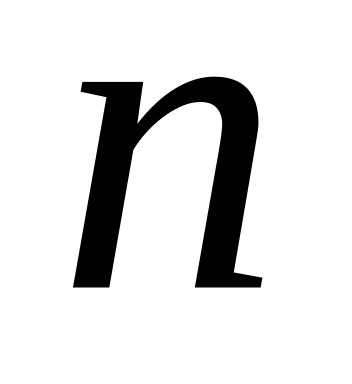3. Рассмотреть применение «правой» обратной матрицы к решению систем линейных уравнений. При выполнении задания обратить внимание на сходства и принципиальные отличия данного случая от случая квадратной невырожденной матрицы.

4. Решить методом «правой» обратной матрицы систему линейных уравнений:

5. _{Привести 4-5 своих примеров.}

Тема 2. Решение систем линейных уравнений над полем вычетов по модулю

Задания

1. Изучить понятие вычетов 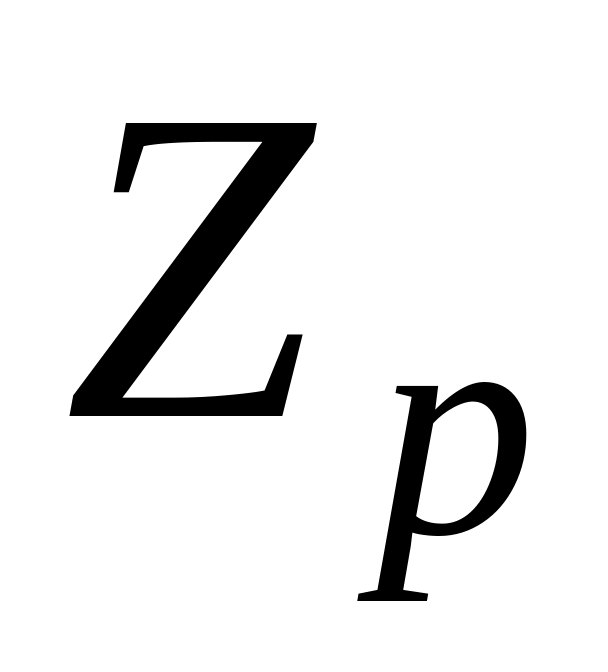по модулю ( – простое).

2. Определить понятие системы линейных уравнений над полем .

3. Разработать методы решения систем линейных уравнений над полем : правило Крамера, метод обратной матрицы, метод Гаусса.

4. Вывести формулу для числа решений системы в зависимости от числа уравнений системы , числа неизвестных и ранга системы .

5. Все исследования иллюстрировать примерами. При выполнении задания обратить внимание на сходство и принципиальные отличия рассматриваемого случая от случая решения систем над полем действительных чисел. Решить систему

Над полем действительных чисел и над полем .

Тема 3. Геометрия 4-мерного куба

Задания

1. Дать определение 4-мерного куба.

2. Найти число вершин, ребер, 3-мерных граней, 2-мерных граней 4-мерного куба.

3. Найти объем 4-мерного куба, объем его 3-мерной грани, площадь его 2-мерной грани, длину ребра.

4. Сделать развертку 3-мерной грани 4-мерного куба.

5. Найти объем 4-мерного гипершара, описанного около 4-мерного куба, и объем гипершара, вписанного в 4-мерный куб.

Тема 4. Ориентированные многоугольники, их площади и применение

Задания

1. Познакомиться с понятием ориентированного треугольника, многоугольника.

2. Познакомиться с понятием площади ориентированного треугольника, многоугольника.

3. Вывести формулу для площади ориентированного треугольника, многоугольника с заданными координатами вершин.

4. Решить задачу: определить количество левых поворотов автомобиля, если маршрут его движения – ломаная с известными координатами вершин. Идея решения: если площадь ориентированного треугольника положительна, то его ориентация положительна, и обратно.

5. Составить программу, позволяющую определить количество левых поворотов автомобиля для любого фиксированного маршрута.

Тема 5. Иррациональность действительных чисел, представимых рядами

Задания

1. Изучить доказательство иррациональности числа при помощи ряда