
- •5 Расчёт валов
- •5.1 Расчёт входного вала
- •5.1.1 Определение реакций в опорах
- •5.1.2 Построение эпюр изгибающих и крутящих моментов
- •5.1.3 Расчёт на статическую прочность
- •5.1.4 Расчёт на усталостную прочность
- •5.2 Расчет промежуточного вала
- •5.2.1 Определение реакций в опорах
- •5.2.2 Построение эпюр изгибающих и крутящих моментов
- •5.2.3 Расчёт на статическую прочность
- •5.2.4 Расчёт на усталостную прочность
- •5.3 Расчет промежуточного вала
- •5.3.1 Определение реакций в опорах
- •5.2.2 Построение эпюр изгибающих и крутящих моментов
- •5.2.3 Расчёт на статическую прочность
- •5.2.4 Расчёт на усталостную прочность
5 Расчёт валов
5.1 Расчёт входного вала
5.1.1 Определение реакций в опорах
Валы редуктора представляют в виде балок, нагруженных внешними силами. Расчётная схема входного вала представлена на рисунке 1.

Рисунок 1 – Расчётная схема
Определение реакций опор в плоскости ZОX.
Сумма моментов относительно опоры 1:
![]() ;
;
![]() Н.
Н.
Сумма моментов относительно опоры 2:
![]() ;
;
![]() Н.
Н.
Определение реакций опор в плоскости ZOY .
Сумма моментов относительно опоры 1:
![]() ;
;
 Н.
Н.
Сумма моментов относительно опоры 2:
![]() ;
;
 Н.
Н.
Реакция в опоре 1:
![]() Н.
Н.
Реакция в опоре 2:
![]() Н.
Н.
Определение реакций по оси Z:
![]() ;
;
![]() Н.
Н.
5.1.2 Построение эпюр изгибающих и крутящих моментов
Построение эпюр изгибающих моментов в плоскости ZОX (рис. 2).
![]() ,
,![]() ;
;

![]() ,
,![]() ;
;
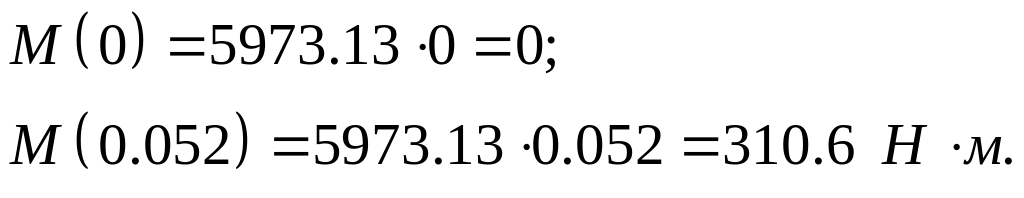
Построение эпюр изгибающих моментов в плоскости ZOY (рис 2).
![]() ,
.
,
.
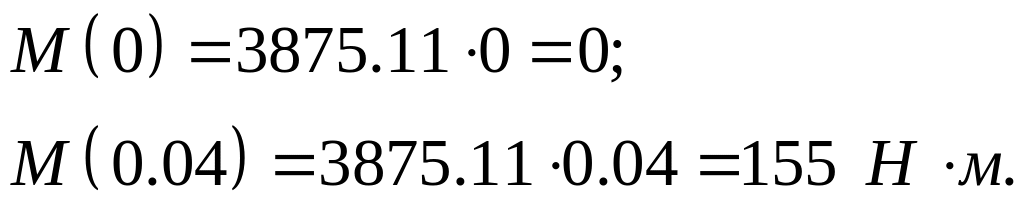
![]() ,
.
,
.
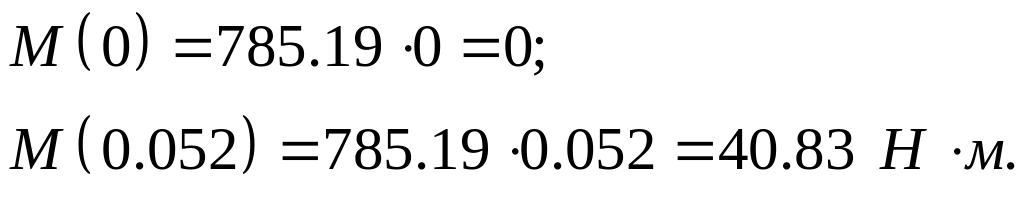
Построение эпюры суммарный изгибающий момент (рис 2):
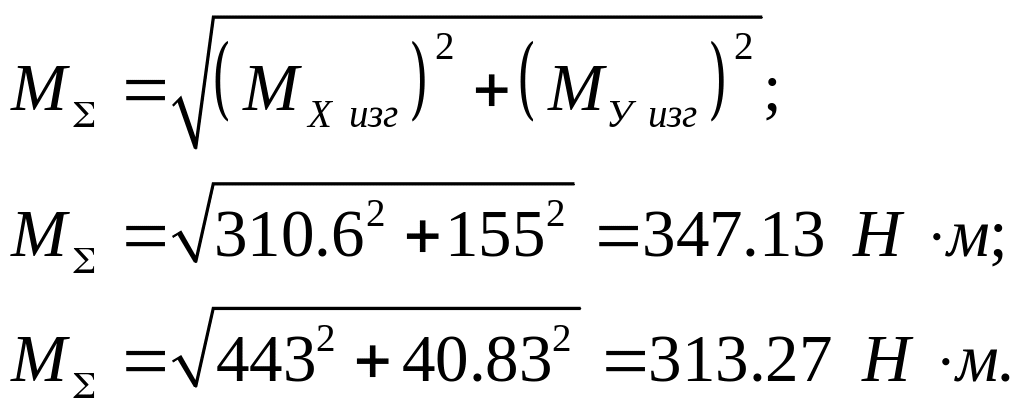
Построение эпюры приведенного момента (рис 2):
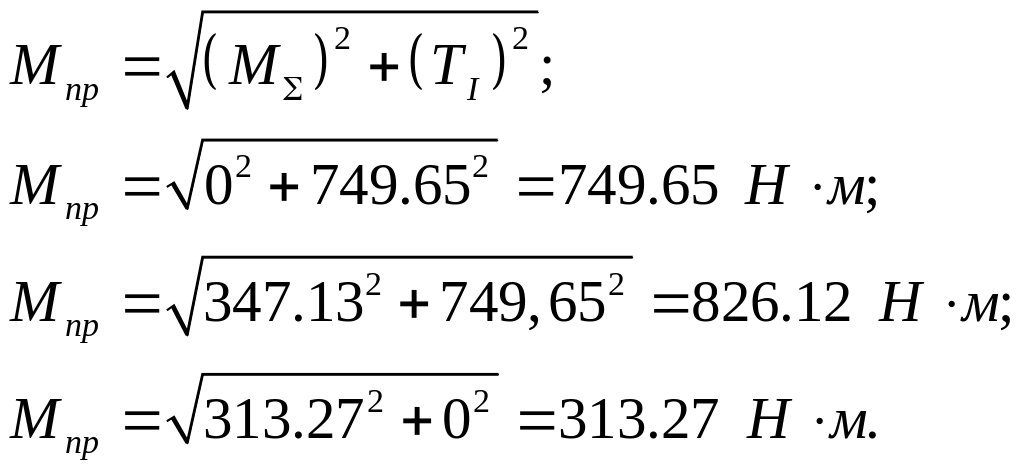
Построение эпюр:

Рисунок 2 – Эпюра крутящих и суммарных изгибающих моментов
5.1.3 Расчёт на статическую прочность
Условие статической прочности:
 ,
,
где
![]() – приведенный момент,
– приведенный момент,
![]() МПа – допускаемое
напряжение при расчете на статическую
прочность,
МПа – допускаемое
напряжение при расчете на статическую
прочность,
![]() - коэффициент
пустотелости вала.
- коэффициент
пустотелости вала.
В сечении с
максимальным приведенным моментом
![]() кН.мм
и диаметром вала
кН.мм
и диаметром вала
![]() мм
мм
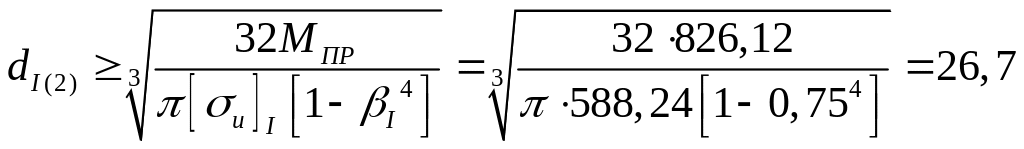 мм,
мм,
![]() – следовательно,
условие статической прочности выполняется.
– следовательно,
условие статической прочности выполняется.
5.1.4 Расчёт на усталостную прочность
Для каждого опасного сечения определяется коэффициент запаса усталостной прочности:
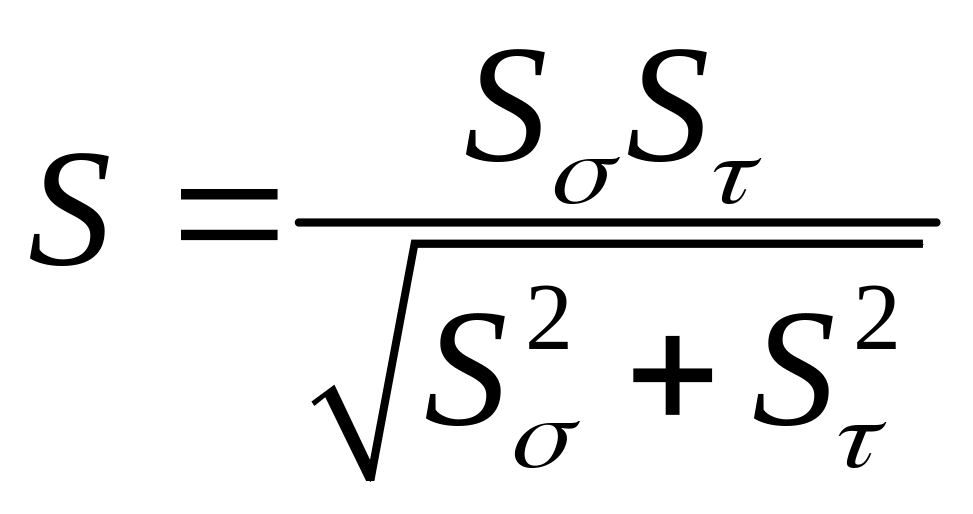 ,
,
где
![]() – коэффициент запаса усталостной
прочности по нормальным напряжениям;
– коэффициент запаса усталостной
прочности по нормальным напряжениям;
![]() – коэффициент
запаса усталостной прочности по
касательным напряжениям.
– коэффициент
запаса усталостной прочности по
касательным напряжениям.
Полученный
коэффициент запаса сравнивают с
допускаемым
![]() .
.
При простом нагружении, когда нагрузки возрастают пропорционально передаваемому крутящему моменту, запасы прочности определяются по максимальным напряжениям:
![]() ;
;
![]() ,
,
где
![]() и
и
![]() – пределы выносливости материала вала
при изгибе и кручении соответственно;
– пределы выносливости материала вала
при изгибе и кручении соответственно;
![]() и
и
![]() – амплитудные значения циклов напряжения
при изгибе и кручении соответственно;
– амплитудные значения циклов напряжения
при изгибе и кручении соответственно;
![]() и
и
![]() – средние значения циклов напряжения
при изгибе и кручении соответственно;
– средние значения циклов напряжения
при изгибе и кручении соответственно;
![]() и
и
![]() – суммарные коэффициенты концентрации
напряжений при изгибе и кручении
соответственно;
– суммарные коэффициенты концентрации
напряжений при изгибе и кручении
соответственно;
![]() и
и
![]() – коэффициенты асимметрии циклов
напряжения при изгибе и кручении
соответственно.
– коэффициенты асимметрии циклов
напряжения при изгибе и кручении
соответственно.
Суммарные коэффициенты концентрации напряжений при изгибе и кручении:
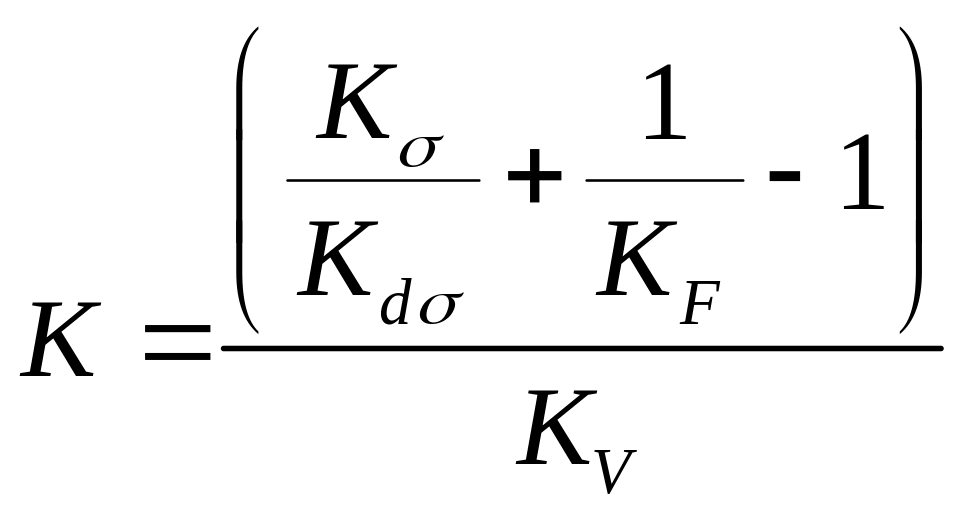 - для нормальных
напряжений;
- для нормальных
напряжений;
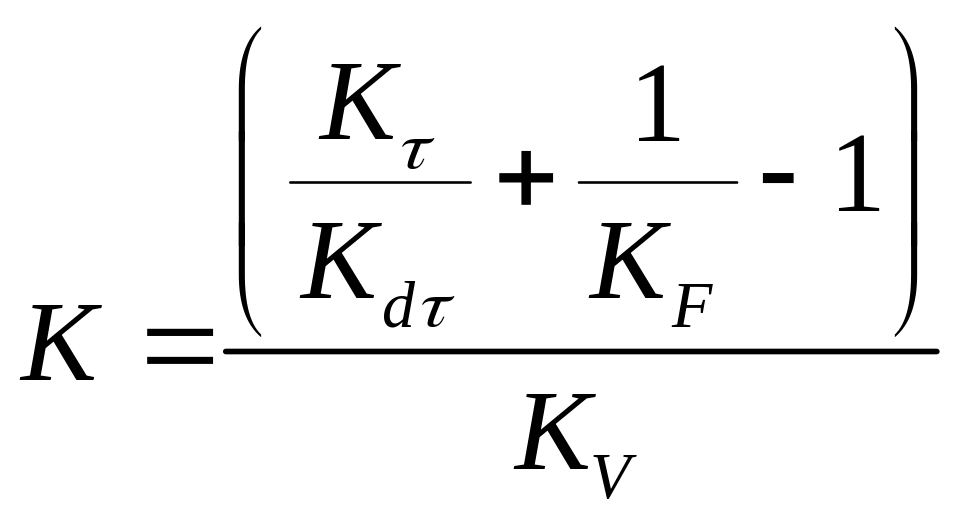 - для касательных
напряжений;
- для касательных
напряжений;
где![]() и
и
![]() – эффективные коэффициенты концентрации
напряжений при изгибе и кручении
соответственно;
– эффективные коэффициенты концентрации
напряжений при изгибе и кручении
соответственно;
![]() и
и
![]() – коэффициенты влияния абсолютных
размеров при изгибе и кручении
соответственно;
– коэффициенты влияния абсолютных
размеров при изгибе и кручении
соответственно;
![]() – коэффициент
шероховатости поверхности;
– коэффициент
шероховатости поверхности;
![]() – коэффициент,
учитывающий влияние поверхностного
упрочнения.
– коэффициент,
учитывающий влияние поверхностного
упрочнения.
Для любого iго сечения:
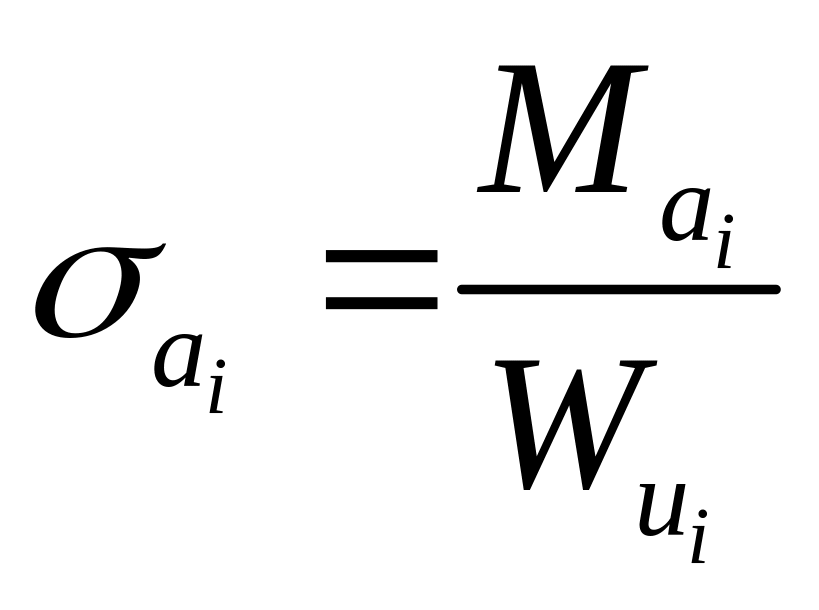 ;
;
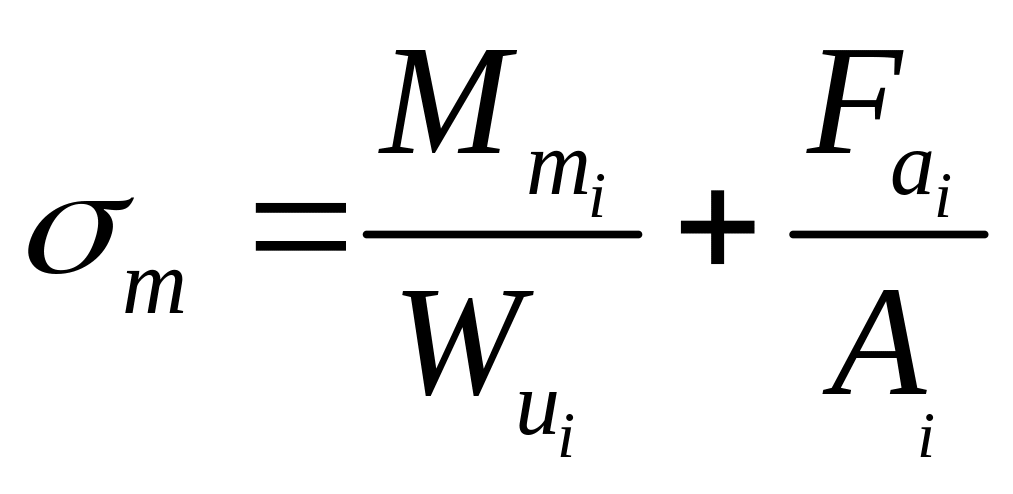 ;
;
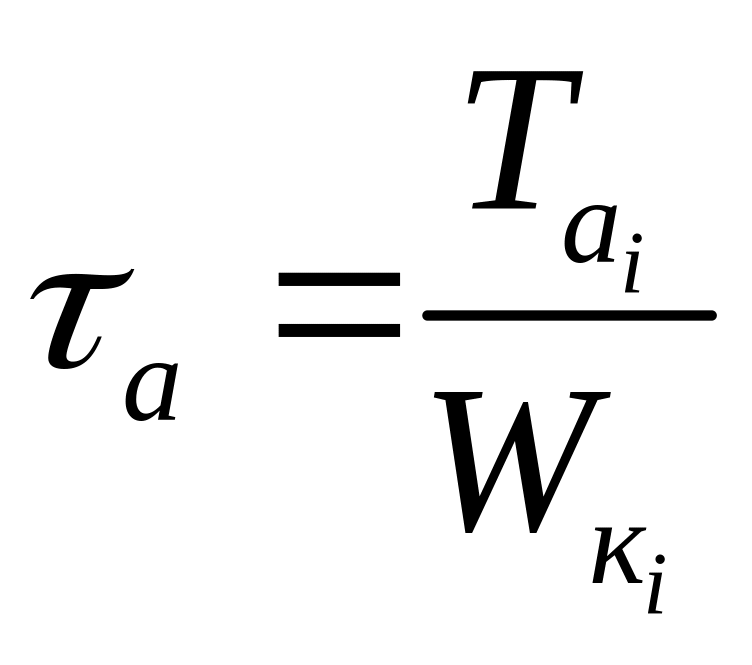 ;
;
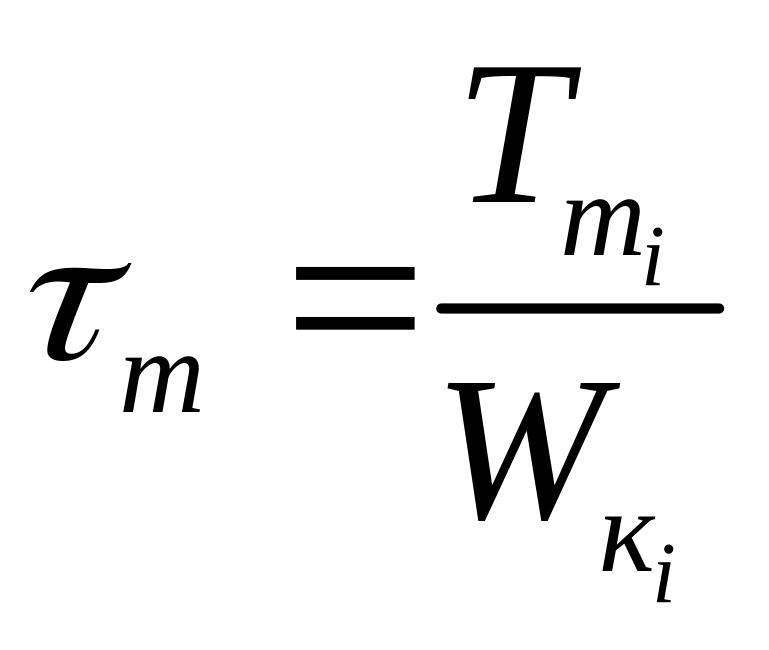 ,
,
где
![]() и
и
![]() – амплитудные значения изгибающего и
крутящего моментов в iтом
сечении соответственно;
– амплитудные значения изгибающего и
крутящего моментов в iтом
сечении соответственно;
![]() и
и
![]() – средние значения изгибающего и
крутящего моментов в iтом
сечении соответственно;
– средние значения изгибающего и
крутящего моментов в iтом
сечении соответственно;
![]() и
и
![]() – моменты сопротивления при изгибе и
кручении в iтом
сечении соответственно;
– моменты сопротивления при изгибе и
кручении в iтом
сечении соответственно;
![]() – осевая сила,
вызывающая напряжения растяжения в
iтом
сечении;
– осевая сила,
вызывающая напряжения растяжения в
iтом
сечении;
![]() – площадь iтого
сечения.
– площадь iтого
сечения.
Средние значения изгибающего момента принимаются равными нулю:
![]() .
.
Средние значения крутящего момента:
![]() .
.
Амплитудные значения изгибающего момента принимаются равными действующим:
![]() .
.
Амплитудные значения крутящего момента:
![]() .
.
![]() МПа – предел
прочности;
МПа – предел
прочности;
![]() МПа – предел
выносливости при изгибе;
МПа – предел
выносливости при изгибе;
![]() МПа – предел
выносливости при кручении;
МПа – предел
выносливости при кручении;
![]() – минимально
допустимый запас прочности;
– минимально
допустимый запас прочности;
![]() – доля дополнительного
крутящего момента от крутильных
колебаний.
– доля дополнительного
крутящего момента от крутильных
колебаний.
Определение запаса прочности в сечении 1 – галтели радиуса r=2 мм.
![]()
![]() мм3.
мм3.
![]() кН.мм.
кН.мм.
![]() кН.мм.
кН.мм.
![]() кН.мм.
кН.мм.
![]() кН.мм.
кН.мм.
![]() кН.
кН.
![]() мм2
мм2
![]() МПа.
МПа.
![]() МПа.
МПа.
![]() МПа.
МПа.
![]() МПа.
МПа.
В зависимости от
![]() ,
,
![]() и предела прочности определяем
и предела прочности определяем
![]() ;
;
![]() .
.
В зависимости от наименьшего диаметра и типа стали определяем
![]() ;
;
![]() .
.
В зависимости от предела прочности и качества поверхности вала определяем
![]() .
.
В зависимости от предела прочности определяем
![]() ;
;
![]() .
.
В зависимости от упрочнения определяем
![]()
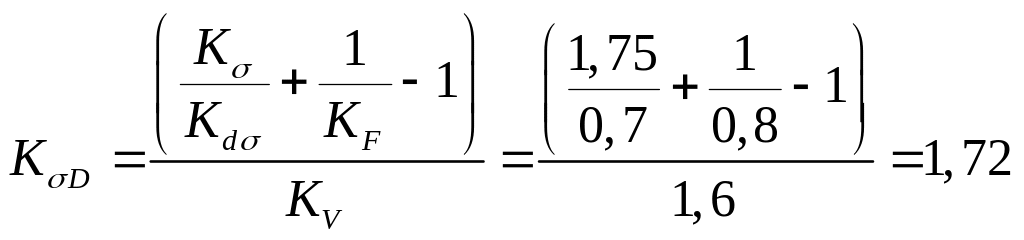 .
.
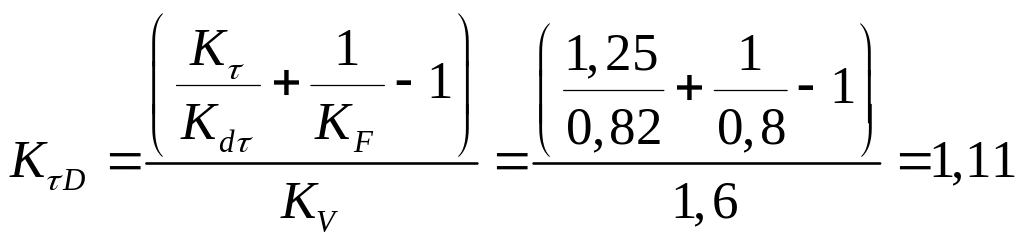 .
.
![]() .
.
![]() .
.
 .
.
Определение запаса прочности в сечении 2 – галтели радиусом r=3 мм.
мм3.
кН.мм.
кН.мм.
кН.мм.
![]() кН.мм.
кН.мм.
![]() Н.
Н.
![]() МПа.
МПа.
![]() МПа.
МПа.
![]() МПа.
МПа.
![]() МПа.
МПа.
В зависимости от , и предела прочности определяем
![]() ;
;
![]() .
.
В зависимости от наименьшего диаметра и типа стали определяем
;
.
В зависимости от предела прочности и качества поверхности вала определяем
.
В зависимости от предела прочности определяем
;
.
В зависимости от упрочнения определяем
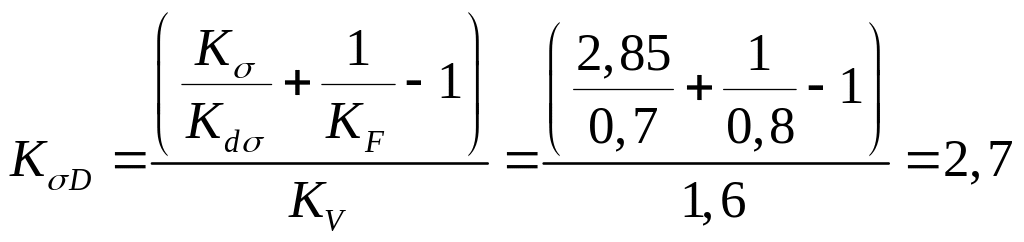 .
.
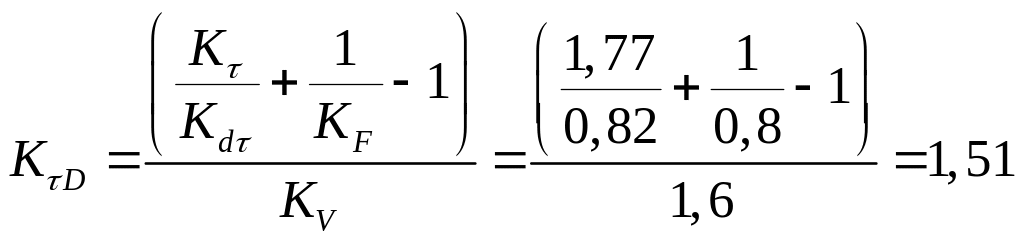 .
.
![]() .
.
![]() .
.
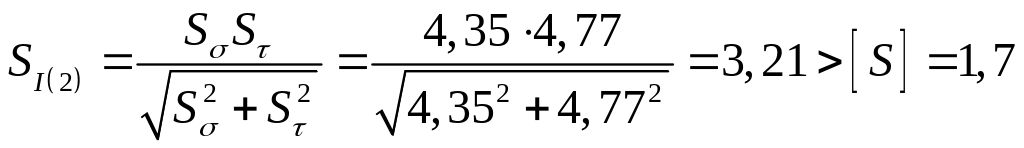 .
.
