1. Крамер ережесі

n белгісізді сызықтық n теңдеулердің жүйесі берілсін

₁₁x₁ + … + _1nx_n = ₁

. . . . . . . . . . (1)

_n1x₁ + … + _nnx_n = _n,

сонымен бірге оның негізгі А = 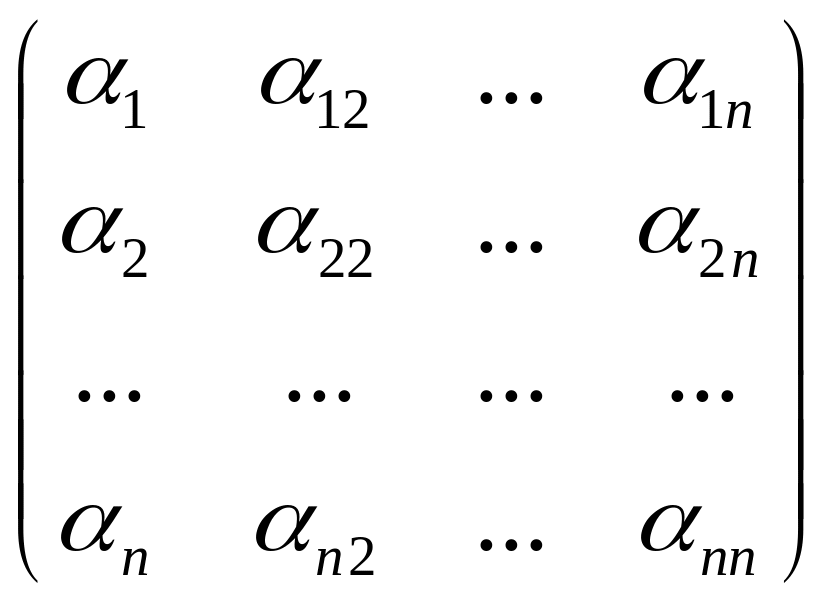матрицасы ерекше емес болсын.

Онда жүйенің матрицалық түрі AX = b болады, мұндағы b = бос мүшелердің бағаны және X = , белгісіздердің бағаны. Жүйенің жалғыз шешімі X = A^–1b формуласымен табылады. Осыдан,

=  ,

яғни

x₁ = (A₁₁₁ + A₂₁₂ +…+ A_n1_n),

x₂ = (A₁₂₁ + A₂₂₂ +…+ A_n2_n),

                 

x_n = (A_1n₁ + A_2n₂ +…+ A_nn_n).

Теорема 1 (Крамер ережесі). Егер n белгісізі бар n сызықтық теңдеулер жүйесінің негізгі матрицасының анықтауышы нөлден өзгеше болса, онда жүйенің жалғыз шешімі болады және шешім

x₁ = , x₂ = ,…, x_n = .

формулаларымен беріледі, мұндағы | A_i | анықтауышы | A | анықтауышының i-бағанын бос мүшелер бағанымен ауыстырғаннан кейін шыққан анықтауыш.

3.Берiлген және түзулердiң арасындағы сүйiр бұрышты табыңдар.

1. Канондық теңдеу

2. 

№9 Билет

Математиканы оқытуды ұйымдастыру. Сабақ, оның құрылымы. Сабаққа қойылатын негізгі талаптар. Сабақтың түрлері.

Сабақ оқыту жұмысын ұйымдастырудың мақсатын, мазмұнын, оқытудың әдістері мен жабдықтарын сипаттайды.

Мұғалім сабақта жалпы топтық және оның дара формасындағы бүкіл оқу процесін басқарады. Оқу процесін ұйымдастырудың жоғарыда көрсетілген түрі сабақта әр түрлі реттілікпен және әр түрлі үйлесімдікпен қолданылады. Қазіргі жағдайда оқыту процесі тиімді түрде білім, білік дағдысын қалыптастыру, ұжымдағы қарым – қатынас т.б. үйлесімді түрде ұйымдастыру формасы қолданылады. Сабақта уақыттан ұту, бірін–бірі оқыту жағдайын тудыру, жеке бастың дамуына айтарлықтай ықпал жасау сияқты оқытудың ұжымдық формасы үлкен роль атқарады.

Сабақтың құрылымы -деп оның тұтастығы мен әр алуан варианттылығын, негізгі көріністерінің сақталуын қамтамасыз ететін сабақ элементтерінің жиынтығын айтады.Сабақ құрылымы қойылған мақсатқа, оқу материалының мазмұнына, қолданылатын оқу әдістері мен тәсілдеріне, оқушылардың дайындық деңгейіне және оқу

процесінде сол сабақтың алатын орнына байланысты анықталады. Сабақ құрылымы әр алуан болады. Тіпті параллель сыныптарда өткізілетін сабақтардың құрылымы бір-бірінен өзгеше болуы мүмкін. Жоғарыда көрсетілген факторларға байланысты сабақтың құрылымы ұдайы өзгеріп, сыныпқа бейімделіп тұрады. Әр сабақта әрбір мұғалімнің өзіне тән қолтаңбасы көрінеді.

Алайда бұл жоспарды ұдайы сақтауға болмайды, сыныптың

ерекшелігіне, оқушылардың дайындық дәрежесіне және т.б. факторларға байланысты ол өзгеріп, кемелдендіріліп отырады.

Математика сабағының құрылымы ұғымын пайдалана отырып, көптеген мүмкін жағдайлар ішінен сабақтың негізгі кезеңдерін бөліп аламыз:

1. Сабақтың мақсатының қойылуы;

2. Жаңа материалмен таныстыру;

3. Жаңа материалды бекіту, а) ақпаратты еске түсіру және сондағы әрекеттің тәсілі;

б) білімін көтеру, оны шығармашылықпен қолдана білу;

4. Оқушының білім, білік дағдысын тексеру;

5. Алынған білімді жүйелеу және жалпылау (тақырып, тарау бойынша).

Сабаққа қойылатын ең негізгі талаптардың бірі – оның мақсаттылығы. Сабақтың мақсаты оқушыға түсінікті болуы керек.

Сабаққа қойылатын екінші бір басты талап – сабақ мазмұнын

дұрыстап орналастыра білу. Математика сабақтарындағы ең маңызды мәселе–оның мазмұны. Қарастырып отырған пәнді логикалық тұрғыда терең бейнелеу керек. Тек математика сабағының мазмұны арқылы білім, білік, дағды қалыптасады және математикалық фактілерді, математикалық әдістерді қолдану арқылы сабақ мазмұнын дамытуға болады. Сондықтан әрбір сабақтың негізгі мазмұнын білу арқылы, солардың төңірегінде материалдар жинастыру керек.

Сабаққа қойылатын үшінші талап – сабаққа қажетті жабдықтар мен әдістерді, оқытудың тәсілдерін, сабақ кезінде тәрбие берудің тиімді әдістерін таңдап алу.

Математика сабақтарында әр түрлі күрделі мәселелерді жай түрде

баяндағанда суреттер мен сызбалар қарастырылатын негізгі ұғымды

сипаттайтын көрнекіліктер қолданылады.

Сабаққа қойылатын төртінші талап – оқушылардың оқу әрекетін әр түрлі формада ұйымдастыру. Өз бетінше білім алу, өзін-өзі бақылау, бағалау, оқу әрекетін жекеше ұйымдастыруды дамыту талабын алға қояды және сабақтарда оқушылар көрнекіліктерді қолданады және топтық жұмыс формасын пайдаланады.

Сабаққа дайындалу – күрделі де қиын жұмыс, сабақ өз деңгейінде өту үшін мұғалімнің әдістемеден жақсы теориялық білімі және дұрыс дайындығы мен сабақты жоспарлай алатын дағдысы болу керек.

Сабақ жоспарын жасау, сабақты ұйымдастыру мен бағдарламалық материалды оқыту мұғалімнен қажырлықты талап етеді. Мұғалімнің сабаққа дайындығы

үш кезеңнен тұрады.

1) мұғалімнің жаңа оқу жылына дайындығы.

2) мұғалімнің тақырыптық дайындығы.

3) мұғалімнің күнделікті сабаққа дайындығы.

Мұғалімнің жаңа оқу жылына дайындығы. Алдымен мұғалім жаңа оқу жылының басында оқу бағдарламасымен, мектеп оқулығындағы оқу материалымен танысып, оқушыларды неге оқытатыны анықтайды. Оқу материалының мазмұнының жобасы бойынша жылдық жоспарын жасайды. Оқу процесінің жылдық жоспарында оқу материалы тоқсандарға бөлініп,

тақырыптарды оқытуға бөлінетін сағат саны мен уақыты белгіленеді, қайталау мерзімі мен тәсілдері анықталады. Оқушыға, мұғалімге керекті әдебиет тізімін жасайды, оқулықтарға талдау жасап, алдағы жұмыстарды жоспарлайды. Оқу жылының басында кабинетт жабдықтайды,

бағдарламаға сай оқулықтар, дидактикалық материал, жұмыс дәптері, есептер жинағы таңдап алынады.

Мұғалімнің тақырыптық дайындығы. Тақырыптық жоспар нәтижесінде әрбір тақырыптың өзекті мәселелерін сабақтарға бөліп, қайталаудың түрлерін, бақылау жұмыстары мен үй тапсырмаларының мазмұнын анықтайды. Тақырыптық жоспар әр сабаққа арналған дидактикалдық материалды, көрнекі құралдар мен техникалық құралдарды уақытында даярлауға мүмкіндік береді, өткізілетін сабақ пен сыныптан тыс жұмыстардың сипатын анықтауға көмектеседі. Сабақтың тақырыптық жоспары оқушылардың жас ерекшеліктеріне және басқа да факторларға сай өңделіп, жетілдіріліп отырады.

Мұғалімнің күнделікті сабаққа дайындығы – күнделікті сабақ жоспарын жасау. Сабақ жоспарын жасау сабақ мазмұнын, баяндау ретін, өздігінен орындайтын жұмыстарды, үйге берілетін тапсырмаларды, сабақта қойылатын сұрақтарды т.с.с. мұғалімнің алдын ала болжауына көмектеседі.

Сабақ мақсатына мынадай талаптар қойылады:

1. Сабақ мақсаты: оқушылар қандай білімді меңгеруі керек (білімділік мақсаты), қандай іскерліктер қалыптастырылды (дамытушылық мақсаты),

сабақтың оқушыларды тәрбиелеуге қосқан үлесі қандай (тәрбиелік мақсаты) тәрізді мәселелерге жауап беруі тиіс.

2. Сабақ мақсаты өте дәл тұжырымдалуға тиіс, яғни сабақта қандай білім, іскерлік пен біліктілік қалыптастырылатыны, тәрбиелік қызметінің мәні белгіленуі керек.

Төменде күнделікті сабақ жоспарын құрудың бір түрі келтірілген

(ұсынылған).

1. Сабақтың тақырыбы.

2. Сабақтың мақсаты.

3. Сабақтың түрі.

4. Сабақтың көрнекілігі.

5. Сабақтың барысы: а) ұйымдастыру кезеңі, б) үй тапсырмасын

тексеру,

в) жаңа сабақты түсіндіру, г) сабақты бекіту, д) сабақтың қорытындысы, е) үйге тапсырма.

Математика сабағын талдау. Өзінің немесе әріптесінің жұмысына

бақылау жасау үшін мұғалім сабақты талдай білуі керек. Сабаққа талдау жасау арқылы өзінің немесе әріптесінің қызметіндегі кемшіліктер мен жетістіктерді бақылап, өзі үйренеді. Математика сабағын талдау мынадай түрде жүргізілуі мүмкін.

1. Жалпы мағлұматтар: сынып, тақырып, мақсаттар, сабақтың түрі,

құрылымы.

2. Сабақтың басталуы (ұйымдастыру кезеңі): формасы, ұзақтығы,

тиімділігі.

3. Үй жұмысын тексеру: оның мақсаты. Қалай тексерілді? Үй

жұмысын тексерудің ұзақтығы, тиімділігі.

4. Сұрақтар мен тапсырмалардың қойылуы мен мазмұны. Бағалар

қалай қойылды? Қойылған бағаның оқушының білім деңгейі мен біліктілігіне сәйкестігі. Мұғалімнің дұрыс және бұрыс жауаптарға әсері.

5. Оқушылардың алдына сабақтың мақсаты қойылды ма? Жаңа

материалдың мазмұны мен көлемі. Баяндау әдісі. Көрнекі құралдарды қолдану. Оқулықпен жұмыс, оның қажеттілігі мен тиімділігі. Сабақтың негізгі маңызды жерін бөліп көрсету.

6. Оқығанды тиянақтау. Оның қорытындысы неде? Сұрақтардың,

есептердің таңдап алынуы және олардың көлемі, есептермен жұмыс жасау әдісі. Өзіндік жұмыс болды ма? Оның ұйымдастырылуы, мақсаты.

7. Келесі сабаққа тапсырма. Оның мақсаты. Мазмұны мен көлемі.

Оқушылардың тапсырманы түсінігіне мұғалімнің көзі жетті ме? Тапсырманы орындау сабақтың мазмұны және әдістемесімен қамтамасыз етілді ме?

8. Мұғалім сабақты қалай аяқтады. Сабақ жоспарының орындалуы.

Мақсатқа қол жетуі.

9. Қорытындылар мен ұсыныстар.