3.Теңдеулер жүйесін шешіңдер:

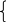(3 – i)x + (4 + 2i)y = 2 + 6i,

(4 + 2i)x – (2 + 3i)y = 5 + 4i.

7-сұрақ

Математиканы оқытудың психологиялық негіздері. Математиканы оқытудың педагогикалық негіздері.Оқушыларды математиканы оқыту барысында тәрбиелеу. Оқушылардың математикаға танымдық қызығушылығын қалыптастыру.

Психологиялық-педагогикалық тұрғыдан саралаудың қорытынды мақсаты – әрбір оқушының жасырын жатқан дарынын оятуға, қызығушылығы мен қабілеттерін барынша дамытуға негізделген даралау болып табылады. Оқытудағы саралаудың психологиялық-педагогикалық ұйымдастырушылық негіздері Қоғамның барлық балалардың дарындарының ашылуына тиімді жағдайлар жасау мен олардың қабілеттіктерін барынша дамытуға деген ынтасы оқытуды саралау қажеттілігіне әкеледі.

Оқытудағы саралаудың психологиялық-педагогикалық ұйымдастырушылық басқа бір негізі оқушылардың қабылдауы тиіс білім көлемінің артуына байланысты болып отыр. Ғылымның тез қарқынмен дамуы білімнің үздіксіз үлғаюына әкеледі. Жаңа білімнің неғұрлым мәнді құраушылары білім беру аймағына келіп түседі. Бұл мектеп бағдарламаларындағы оқу материалдарының үздіксіз көбеюіне әкеледі.

Осылардың ішіндегі көрнекілік принципі туралы: көрнекілік принципін алғаш зерттеп, оған мәнді үлес қосқан Я.А.Коменский, К.Д.Ушинский т.б. Осы принцип негізінде алғаш оқытудың әдістемесін жазды. К.Д.Ушинский көрнекілік жайындағы ілімді дамыта келіп, көрнекілік- балалардың психологиялық ерекшеліктеріне жауап береді, балалар заттардың пішіні, дыбысы, бояуы арқылы ойлайды деді.

Оқыту процесінде сөзбен іс, теория мен практика озара байланыста болады.Әртүрлі көрнекілік қолданудың нәтижесінде сабақ әрі түсінікті, әрі қызықты болып өтеді. Мысалы, жоғары сыныптарда сабақты демонстрациялап өткізу өте тиімді және нәтижелі болады. Көрнекілік абстракты ұғымды игеруге әсер етеді. Сонымен, көрнекілік принципінің оқыту материалдарын, әсіресе, теориялық ережелерді терең оқуда, берік есте сақтауда алатын орны ерекше.

Көрнекілік түрлері: Табиғи көрнекілікке коллекциядағы кептірілген өсімдіктер, хайуандар мен құстардың тұлыбы, минералдар және т.б. жатады. Заттармен бейнелеу көрнекілігі: муляж, геометриялық фигура, макет, портреттер, архитектура, кескіндеме және мүсін үлгілері, жер бетінің бедеріт.б. Симболикалық көрнекілікке : қатарлар, карто- граммалар, схемалар, диаграммалар, кестелер жатады. Мысалы кестенің бірнеше түрлері бар. Олар: хронологиялық, синхрондық, тақырыптық, графикалық кестелер.

Экранды-динамикалық көрнекілік шындық дүниені бейнелейді. Олар: диапозитивтер, диафильмдер, эпипроекциялар, оқу киносы, оқу теледидары. Дыбысты техникалық көрнекілікке аудио дискілер, радиоқабылдағыштар жатады. Көрнекі құралдар оқу материалдарын, әсіресе, теориялық ережелерді есте жақсы сақтау және жеңіл түсіну үшін қолданады.[5].

Математиканы оқыту әдістемесі педагогика ғылымының бір саласы

болып есептелетін жалпы және жас ерекшелік психологиясымен тығыз

байланыста болады. Оқыту және тәрбиелеу процесі оқушылардың жас

ерекшеліктеріне қарай жүргізілгенде ғана нәтиже бермек. Сондықтан

балалардың психологиясының заңдылықтарын жете білу, оқыту мен

тәрбиелеудің неғұрлым тиімді түрлері мен жолдарын табуға көмектеседі.