1 - сұрақ
Таңдап алған тақырып бойынша дифференциалды оқытуды ұйымдастыру.
Таңдап алған тақырып бойынша дифференциалды оқытуды ұйымдастыру.
Дифференциалды оқыту технологиясы
Дефференциал оқыту дегеніміз-оқушылардың псих-қ ерекшеліктеріне қарай топтарға бөу, яғни әр оқушыны жекеленген қабілетіне қарай топтастыру. Дифф-қ оқытуда топтарға түрлі ерекшеліктерге қарай бөледі.
1.Псих-қ ерекшелік:
2.Оқу үлгерімі бойынша:
3.Бағдарына қарай
Дифф-қ оқыту –нашар оқитындардың деңгейін көтерудің, және күрделі тапсырма беру арқылы ой белсенділігімен ерк жігерлігін арттырып, отырудың тиімді жолы.
Дифференциалды оқыту сабаққа қалай енгізетіні, бөлінетіні және қандай деңгейлік тапсырма берілетіні туралы өз пікірлерін ортаға салады.
Дифференциацияның мәні – оқушыларды бөлу емес, оларды біріктіруде дер кезінде дифференциалды көмек көрсету.
Өз пікірін негіздеп, дәлелдеуді талап етуге;
• Білім беруде оқушыны дәлелдерге мән беруге ынталандыру, шағын топтарда жұмыс істеу әдістерін тиімді қолдануға;
• Ойлау мен оқыту тәжірибесіне енгізуде, ақпараттар жинауда сын тұрғысынан талдау мен бағалаумен танысады.
2.Қалыпты үлестірім функциясы. Кездейсоқ шамалар жайында жалпы түсінік. Дискреттік кездейсоқ шамалар.Кездейсоқ шамалардың ықтималдық тығыздығы. Кездейсоқ шамалардың тәуелдігі.
Қалыпты үлестiрiм заңдылығы.
Анықтама.
аралығынан мән қабылдайтын және
ықтималдықтар тығыздығы
немесе
(мұндағы
-
нақты параметрлер) теңдiгiмен анықталатын
Х кездейсоқ шамасын қалыпты үлестiрiм
деп атайды.
Қалыпты үлестiрiмнiң сандық сипаттамалары:
Осымен,
қалыпты үлестiрiмнiң бiрiншi параметрi
-математикалық
күтiм, ал
- орташа квадраттық ауытқуы болды.
Ықтималдықтың қалыпты үлестірім заңы ықтималдық тығыздығы арқылы анықталады
Бұл
жердегі
Кездейсоқ шамалар жайында жалпы түсінік.
Cандық мән қабылдайтын, бiрақ қандай мән қабылдайтынын алдын ала болжап айту мүмкiн болмайтын шамаларды кездейсоқ шама деп атайды.
Кездейсоқ шама - Элементар оқиғалар кеңістігінде анықталған сандық функция.
Кездейсоқ
шамаларды
және басқа да бас әрiптермен, ал олардың
қабылдайтын мәндерiн
және басқа да кiшi әрiптермен белгiлеймiз.
Қабылдайтын мәндер жиынына орай кездейсоқ шамаларды екi топқа бөледi: дискреттiк және үзiлiссiз. Егер кездейсоқ шамалардың мәнiн тiзбек түрiнде жазуға болса, онда оны дискреттiк деп, ал мәндерi белгiлi бiр аралықта жатса, онда оны үзiлiссiз деп атайды.
Дискретті кездейсоқ шама.
Кездейсоқ деп отырған шаманың мәндерін алдын – ал айтуға болмайды. Сонымен кездейсоқ шама дегеніміз сандық мән қабылдайтын, бірақ қандай тиянақты мәнді қабылдайтыны алдын ала айтуға бомайды. ξ,η,... грек алфавитінің әріптері арқылы белгіленеді. Кездейсоқ шамаларды қабылдайтын мәндеріне қарап, оларды екі топқа бөлуге болады: дискретті және үзіліссіз кездейсоқ шамалар. Кездейсоқ шамалар мен кездейсоқ оқиғаларды бір-бірімен ажырата білген жөн. Анықтамадан байқап отырғанымыздай кездейсоқ шама міндетті түрде пайда болады, тек оның қандай мән қабылдайтыны алдын ала белгісіз. Ал кездейсоқ оқиға пайда болуының өзі кездейсоқ жай.
ξ кездейсоқ шаманың қабылдайтың мәндері арқылы бүтін сандар немесе тізбек түрінде жазылса, онда ондай ξ кездейсоқ шамасын дискретті деп атайды. дискретті кездейсоқ шаманы анықтау үшін әдетте таблица құрады. Екі жол болады. Оның бірінші жолында кездейсоқ шаманың қабылдайтын мәндері, ал екінші жолында сол мәндерді қабылдау ықтималдықтары жазылады.
Мәндер ξ |
Х1 |
Х2 |
... |
хn |
Ықтималдықтар. Р. |
P1 |
P2 |
|
pn |
Бұлай құрылған табалицаны ξ кездейсоқ шаманың үлестірім таблицасы деп аталады. Үлестірім таблицасының екі қасиеті бар: 1) екінші жолда тұрған сандар теріс емес. Рi ≥0
2) екінші жолда тұрған сандардың қосындысы бірге тең.
(1)
Анықтама. Кездейсоқ шаманың мәндерi мен олардың ықтималдықтарының арасындағы сәйкестiктi дискреттi кездейсоқ шаманың үлестiрiм заңы немесе үлестiрiм функциясы деп атайды. Бұл сәйкестiк таблица, график және аналитикалық түрде берiлуi мүмкiн.
Дискреттi кездейсоқ шаманың үлестiрiм заңы кесте арқылы берiлуi мүмкiн.
Х |
|
|
|
…. |
|
Р |
|
|
|
.… |
|
Бұл
жерде, бiрiншi жолда кездейсоқ шама
-тың
қабылдайтын мәндерi, екiншi жолда сол
мәндердi қабылдау ықтималдықтары
жазылады.
Кездейсоқ
шама
-тың
мәндерi толық жүйе жасайтын болғандықтан:
.
Егер кездейсоқ шаманың мәндер қабылдау ықтималдықтары Бернулли формуласымен табылса, онда кездейсоқ шама биномиальды үлестiрiлген деп аталады.
Егер кездейсоқ шаманың мәндер қабылдау ықтималдықтары Пуассон формуласымен табылса, онда кездейсоқ шаманың үлестiрiм заңы Пуассон үлестiруi деп аталады.
Кездейсоқ шаманың ықтималдық тығыздығы
А-а
кездейсоқ шамасының үлестірім тығыздығы
деп f(
)
lim
теңдігімен
анықталатын f(
)
функциясын айтады. Үлестірім тығыздықтың
мынандай ықтималдық түсініктемелері
бар.
-ке
қатысты жоғарғы ретті ақырсыз аз шамаға
дейінгі дәлдікпен f(
)
көбейтіндісі
кездейсоқ шамасының мәндері
пен
-тің
арасында жату ықтималдығы береді.
Егер үлестірім тығыздығы У f( ) қисығы түрінде көрсетсек, оның f( ) көбейтіндісі f( ) пен кесінділерінде құрылған тік төртбұрыштың ауданы болады.
А-а
Егер
кездейсоқ шамасы (
)
аралығынан мән қабылдаса және оның
үлестірім тығыздығы f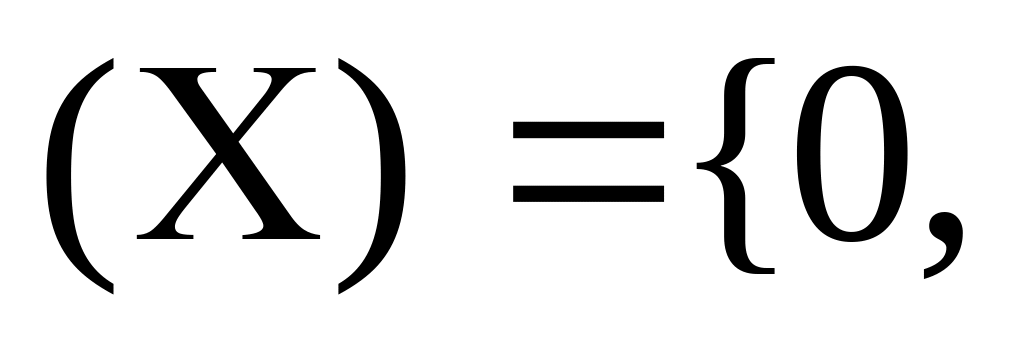
егер
х
,
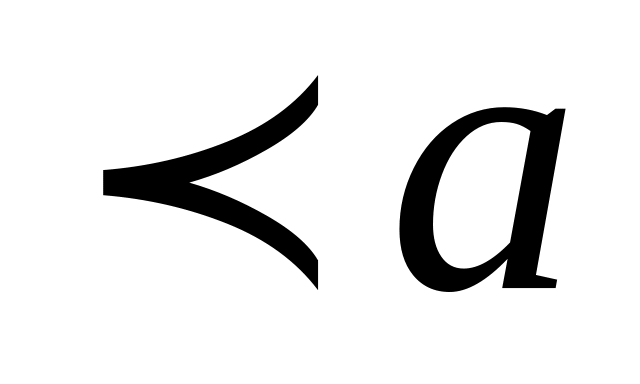
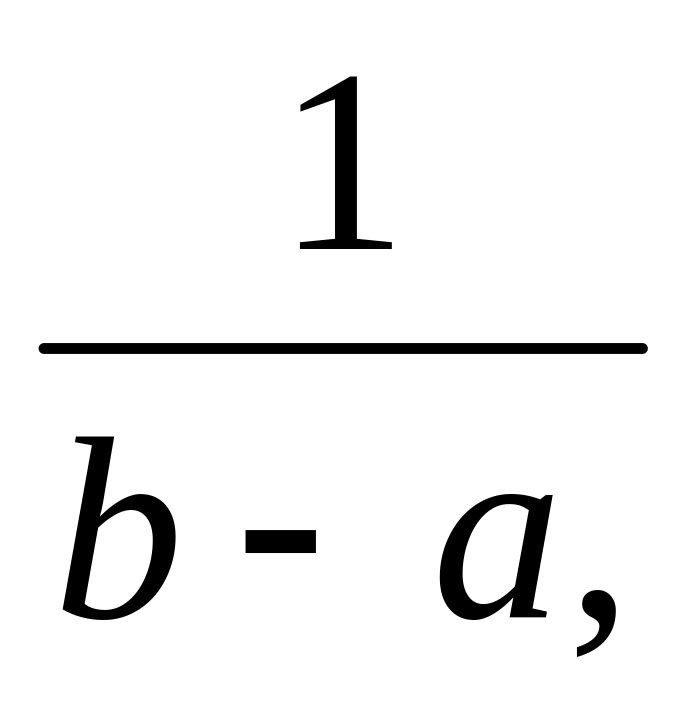егер
0,
егер
теңдігі арқылы орындалса, оның кездейсоқ шамасын бірқалыпты үлестірім заңына бағынады.
А-а
Егер
кездейсоқ шамасы (
)
аралығынан мән қабылдаса және оның
үлестірім тығыздығы
мұндағы
нақты параметрлер, теңдігімен анықталса,
оның
кездейсоқ шамасын қалыпты заң бойынша
үлестірім деп атайды. Параметрлері
және
болатын қалыпты заңды
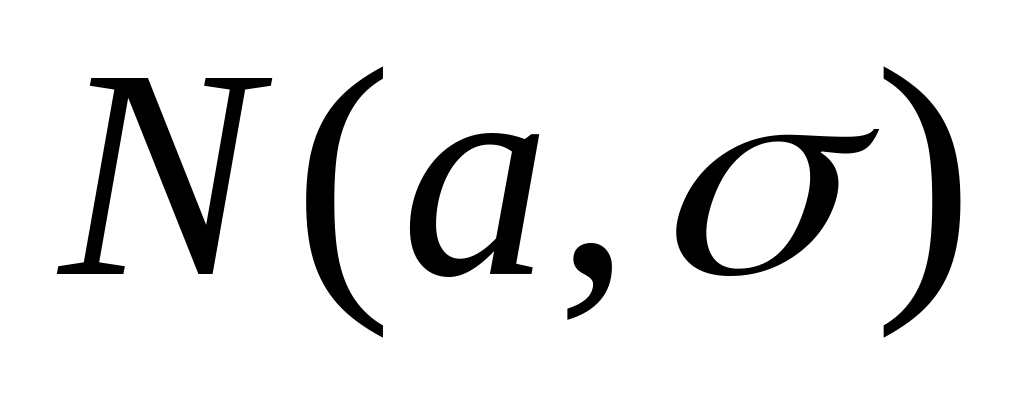арқылы
белгілейміз.
А-а
Егер
кездейсоқ шамасы (
)
интервалынан мән қабылдаса және
үлестірім тығыздығы f(
)
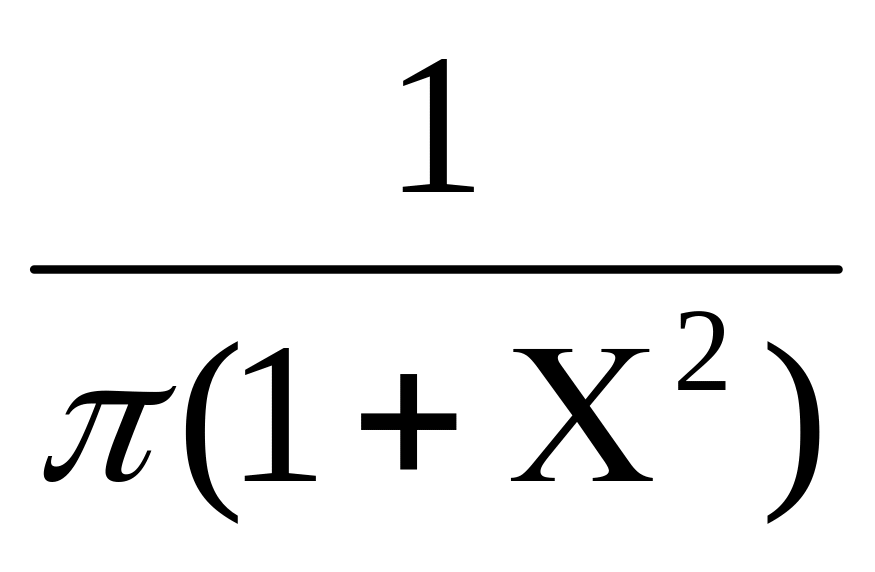теңдігімен анықталса, онда
кездейсоқ шамасы Коши заңы бойынша
үлестірім деп атайды.