
3. Непрерывные случайные величины
● Функция распределения и функция плотности непрерывной случайной величины
Случайная величина
 имеет функцию распределения
имеет функцию распределения .
Найдите плотность вероятности
.
Найдите плотность вероятности случайной величины
случайной величины .
.

Случайная величина
 имеет функцию распределения
имеет функцию распределения .
Найдите плотность вероятности
.
Найдите плотность вероятности случайной величины
случайной величины .
.

Случайная величина
 имеет функцию распределения
имеет функцию распределения .
Найдите плотность вероятности
.
Найдите плотность вероятности случайной величины
случайной величины .
.

Распределение непрерывной случайной величины
 задано плотностью вероятности
задано плотностью вероятности .
Найдите плотность вероятности
.
Найдите плотность вероятности случайной величины
случайной величины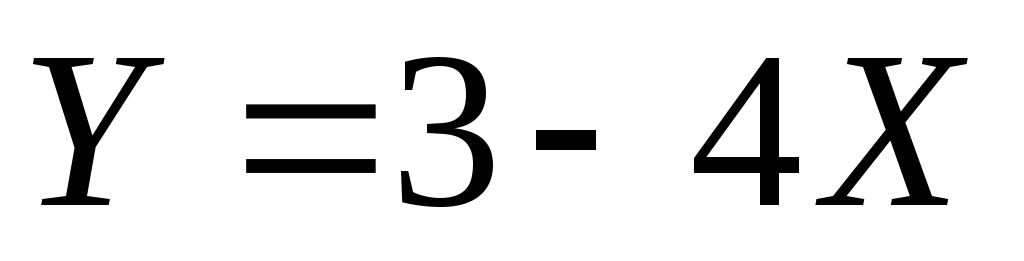 .
.

Случайная величина
 имеет плотность вероятности
имеет плотность вероятности .
Найдите плотность вероятности
.
Найдите плотность вероятности случайной величины
случайной величины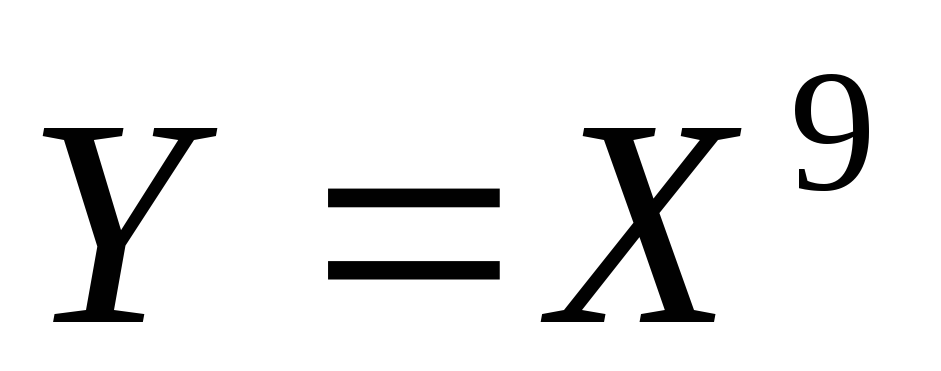 .
.

Случайная величина
 имеет плотность вероятности
имеет плотность вероятности
 Найдите константу
Найдите константу и вероятность
и вероятность .
.

Функция плотности вероятности случайной величины
 имеет вид
имеет вид .
Найдите константу
.
Найдите константу и вероятность
и вероятность .
.

Функция плотности вероятности случайной величины
 имеет вид
имеет вид .
Найдите константу
.
Найдите константу и вероятность
и вероятность .
.

Плотность вероятности случайной величины
 имеет вид
имеет вид .
Найдите
.
Найдите и
и .
.

● Равномерное распределение на отрезке
Случайная величина
 равномерно распределена на отрезке
равномерно распределена на отрезке .
Найдите вероятность
.
Найдите вероятность .
.

Случайная величина
 равномерно распределена на отрезке
равномерно распределена на отрезке .
Найдите вероятность
.
Найдите вероятность .
.

Случайные величины
 независимы и равномерно распределены
на отрезке
независимы и равномерно распределены
на отрезке .
Найдите математическое ожидание
.
Найдите математическое ожидание .
.

Случайная величина
 имеет равномерное распределение на
отрезке
имеет равномерное распределение на
отрезке Найдите коэффициент корреляции случайных
величин
Найдите коэффициент корреляции случайных
величин и
и

Случайная величина
 равномерно распределена на отрезке
равномерно распределена на отрезке .
Найдите математическое ожидание
.
Найдите математическое ожидание .
.

Случайная величина
 равномерно распределена на отрезке
равномерно распределена на отрезке .
Найдите дисперсию
.
Найдите дисперсию .
.

Случайная величина
 равномерно распределена на отрезке
равномерно распределена на отрезке .
Найдите
.
Найдите .
.

Случайная величина
 равномерно распределена на отрезке
равномерно распределена на отрезке .
Найдите
.
Найдите .
.

Найдите математическое ожидание и дисперсию произведения независимых случайных величин
 и
и с равномерными законами распределения:
с равномерными законами распределения: – на отрезке
– на отрезке ,
, – на отрезке
– на отрезке .
.

Случайные величины
 и
и независимые и равномерно распределены
на отрезках:
независимые и равномерно распределены
на отрезках: – на отрезке
– на отрезке ,
, – на отрезке
– на отрезке .
Найдите
.
Найдите .
.

● Показательное распределение
Случайные величины
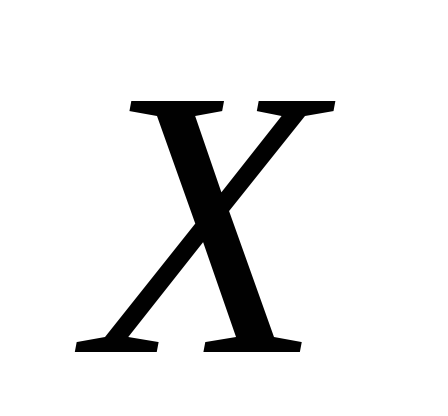 и
и независимые и распределены по
показательному закону, причём
независимые и распределены по
показательному закону, причём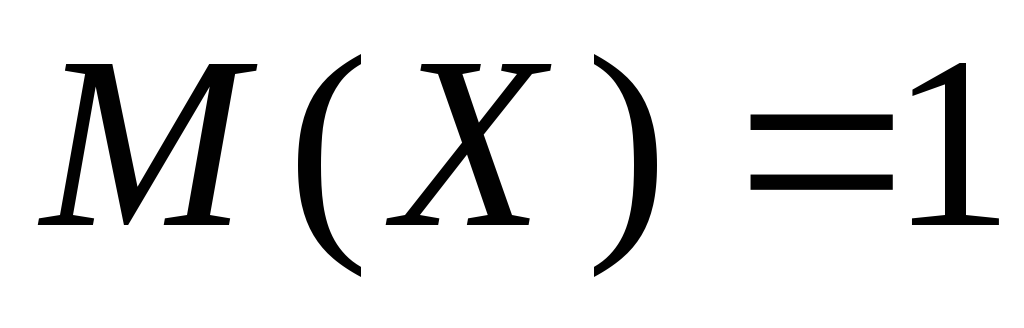 ,
, .
Найдите
.
Найдите .
.

Случайные величины
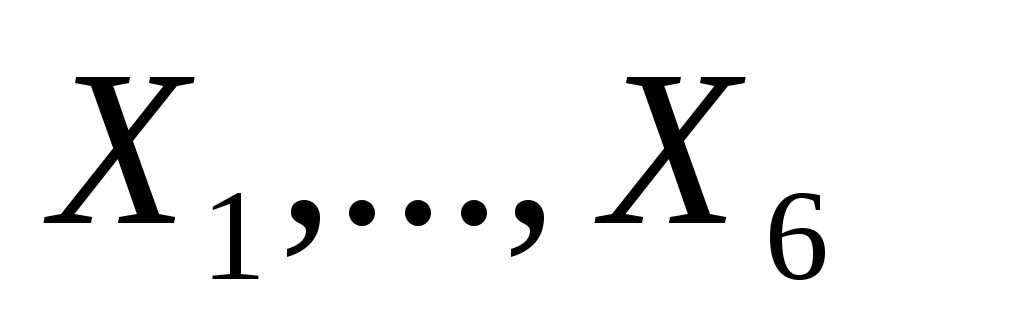 независимы
и распределены по показательному
закону. Найдите
независимы
и распределены по показательному
закону. Найдите ,
если
,
если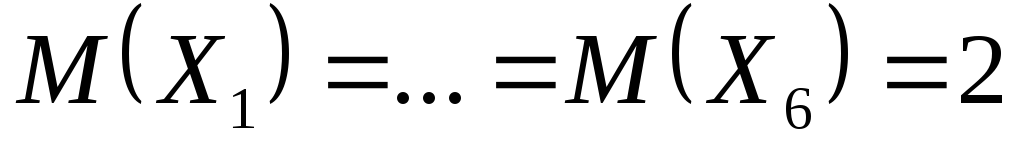 .
.

Случайная величина
 распределена по показательному закону.
Найдите математическое ожидание
распределена по показательному закону.
Найдите математическое ожидание ,
если дисперсия
,
если дисперсия .
.

Случайная величина
 распределена
по показательному закону. Найдите
математическое ожидание
распределена
по показательному закону. Найдите
математическое ожидание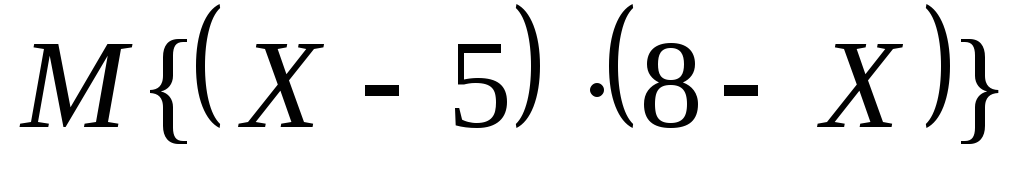 ,
если дисперсия
,
если дисперсия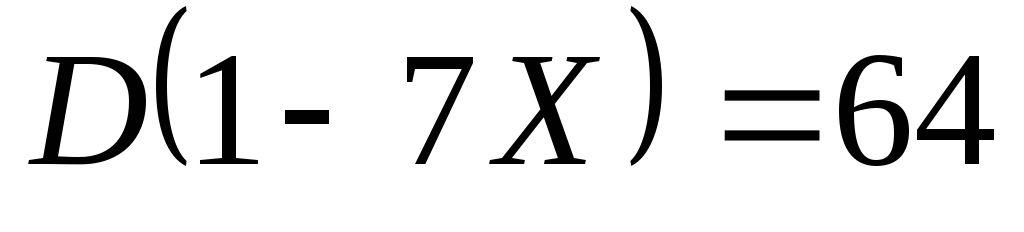 .
.

Случайная величина
 распределена по показательному закону.
Найдите вероятность
распределена по показательному закону.
Найдите вероятность ,
если
,
если .
.

● Нормальное распределение на прямой
Для нормальной случайной величины
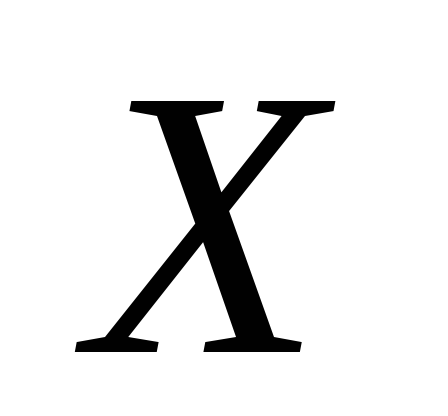 с математическим ожиданием
с математическим ожиданием и дисперсией
и дисперсией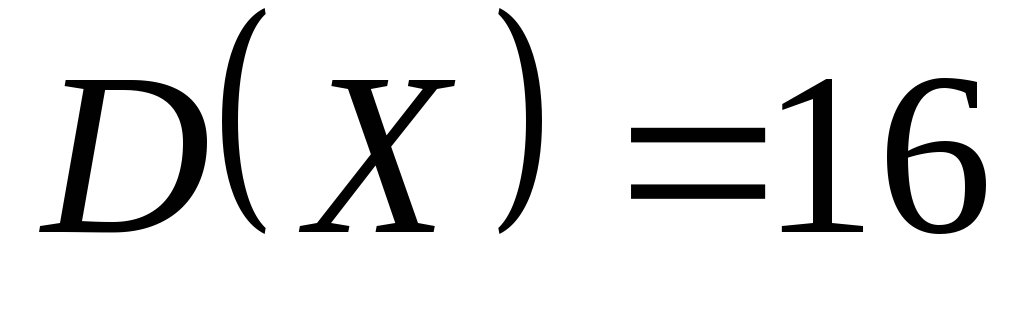 найдите вероятность
найдите вероятность .
.

Случайная величина
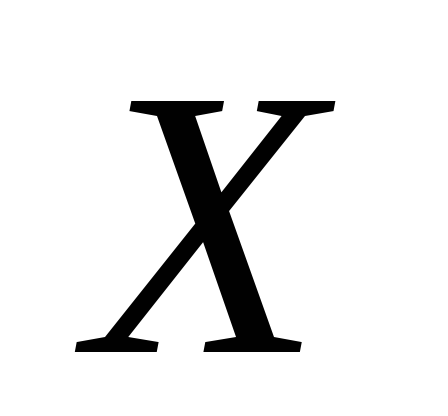 имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами и
и .
Найдите вероятность попадания
.
Найдите вероятность попадания в интервал
в интервал .
.

Для нормальной случайной величины
 известно, что математическое ожидание
известно, что математическое ожидание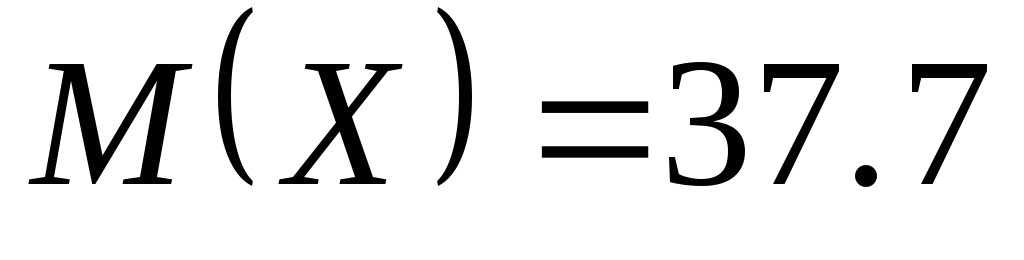 и вероятность
и вероятность Найдите дисперсию
Найдите дисперсию .
.

Для нормальной случайной величины
 известно, что дисперсия
известно, что дисперсия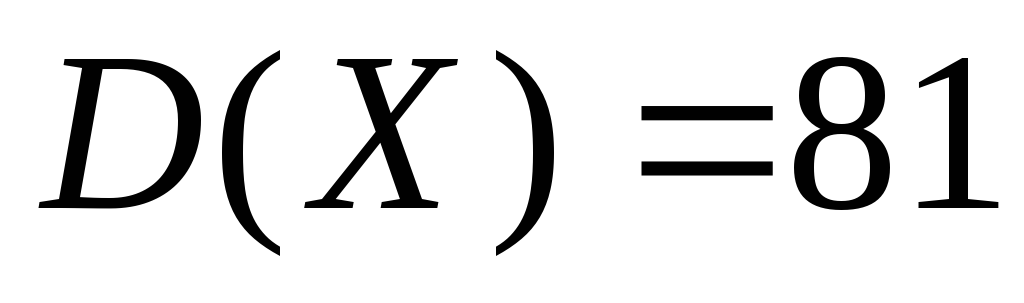 и вероятность
и вероятность .
Найдите математическое ожидание
.
Найдите математическое ожидание .
.

Для нормальной случайной величины
 с математическим ожиданием
с математическим ожиданием и дисперсией
и дисперсией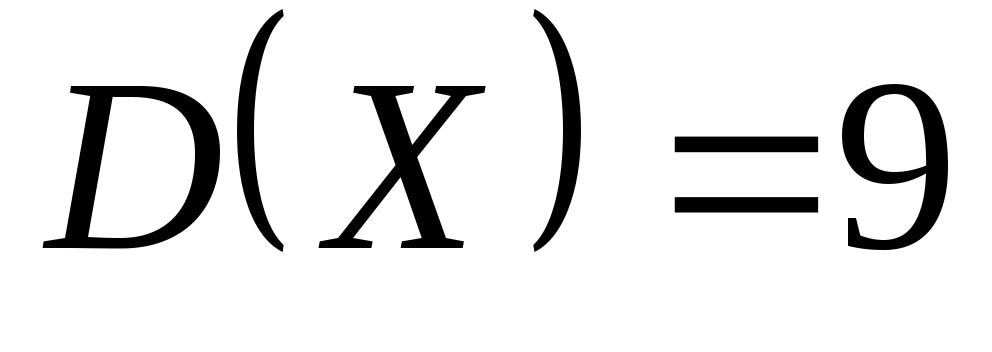 найдите вероятность
найдите вероятность .
.

Математические ожидания и дисперсии независимых нормальных случайных величин
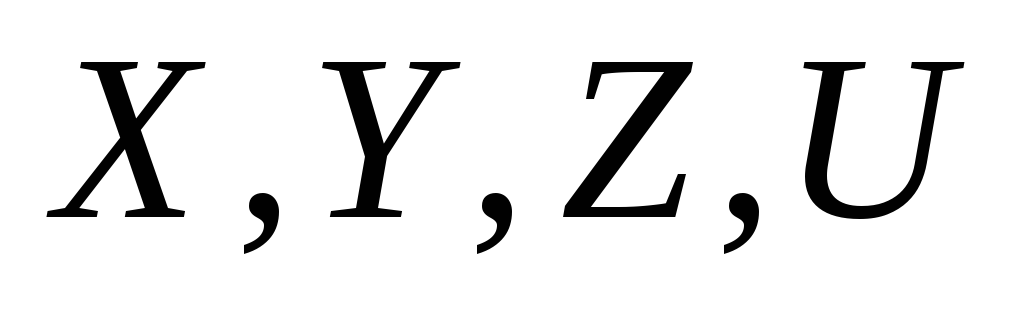 равны 1. Найдите вероятность
равны 1. Найдите вероятность .
.

Для нормальной случайной величины
 с математическим ожиданием
с математическим ожиданием и дисперсией
и дисперсией найдите вероятность
найдите вероятность .
.

Для независимых нормальных случайных величин
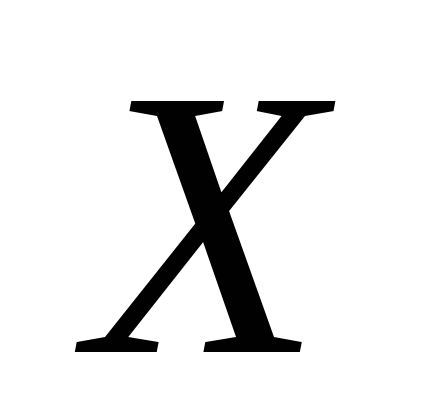 ,
, известны их математические ожидания
и дисперсии:
известны их математические ожидания
и дисперсии:
 ,
,
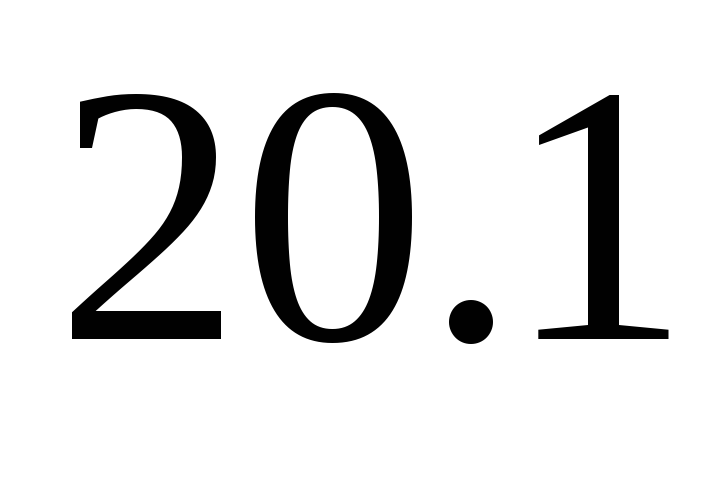 ,
,
 ,
, .
Найдите вероятность
.
Найдите вероятность .
.

Независимые нормальные случайные величины
 имеют одинаковые параметры:
имеют одинаковые параметры: ,
, ,
, .
Для случайной величины
.
Для случайной величины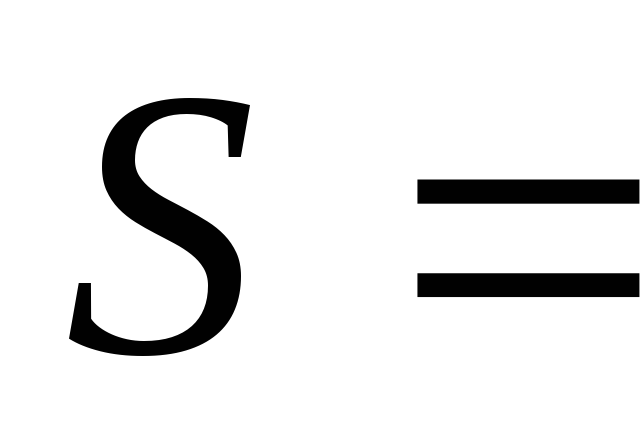
 найдите вероятность
найдите вероятность .
.

Для нормальной случайной величины
 с математическим ожиданием
с математическим ожиданием и дисперсией
и дисперсией найдите вероятность
найдите вероятность .
.

Случайные величины
 и
и независимые и распределены по нормальному
закону, причём
независимые и распределены по нормальному
закону, причём ,
, .
Найдите
.
Найдите .
.

