12. Докажите, что коэффициент корреляции случайных величин х и у удовлетворяет условию .

Определение. Коэффициентом корреляции двух слу­чайных величин называется отношение их ковариации к произведе­нию средних квадратических отклонений этих величин: p_xy=K_xy/«сигма»_х«сигма»_х. Из определения следует, что р_ху=р_ух=р. Очевидно также, что коэффициент корреляции есть безразмерная величина. Отметим свойства коэффициента корреляции.

1. Коэффициент корреляции принимает значения на отрезке [-1;1],т.е. -1<р<1.Из неравенства

Тк As и Ex не меняются при меняющихся заменах, а любое равномерное распределение на отрезке может быть получено линейной заменой из любого другого равномерного распределения, например, из равномерного распределения на отрезке, то достаточно посчитать As и Ex для этого распределения.

As=μ₃/σ³, σ=√D, μ₃=M[(x-M(x)³]

Ex= μ₄/σ⁴-3

Плотность f_x=1/(b-a)=1, μ₃= S^b _a fx(t)tdt== S^b _a tdt=t²/2 в пределах от a до =(b-a)²/2

D== S^b _a fx(t)t²dt=(b-a)³/3

σ=√D=√(b-a)³/3 

As=μ₃/σ³=((b-a)²/2)/( √(b-a)³/3 )

Ex= μ₄/σ⁴-3=((b-a)⁵ /5)/(( b-a)³/3)² - 3

μ₄= M[(x-M(x)⁴] fx(t)tdt= S^b _a t⁴dt=(b-a)⁵ /5

13. Как вычисляется дисперсия в случае распределения с плотностью f (x)? Докажите, что для случайной величины X с плотностьюдисперсия D(X ) не существует, а математическое ожидание M(X ) существует.

Дисперсия абсолютно непрерывной случайной величины.

Дисперсия абсолютно непрерывной случайной величины X с функцией плотности f(x) и математическим ожиданием m = M(X) определяется таким же равенством, как и для дискретной величины

Из равенства (5.26) следует, что справедлива следующая формула

Поскольку формула (5.29) может быть записана в следующем виде

то формулу (5.30) можно представить таким образом

1. 

В случае когда абсолютно непрерывная случайная величина X сосредоточена на промежутке [a, b], формулы (5.30), (5.32) примут вид

1. .

Дисперсия непрерывной случайной величины определяет степень рассеивания значений, принимаемых случайной величиной, вокруг ее математического ожидания.

Среднее квадратичное отклонение, или стандартное отклонение, непрерывной случайной величины X определяется так же, как и для дискретной случайной величины:

Начальным моментом порядка k (k принадлежит N), свободная величина Х называется мат.ожиданием k-й степени Х.

Центральным моментом порядка k СВ Х называется мат.ожидание k-й степени отклонения:

Теорема: если Х и У независимые СВ, то

Док-во:

Докажем связь начальных и центральных моментов:

f(_xy)=d(f_x(x))/dy и наоборот

По определению:

Компоненты Х и У абсолютно непрерывного случайного вектора называются независимыми, если

Пример: прямоугольник , в котором вектор (х,у) равномерно распределен.

F(x;y)= иначе

При решении уравнения найдем

а)

б)

Аналогично для

Компоненты Х и У – независимые

Неравенство Маркова: если x0, a>0, то P(Xa)  M(X)/a

Н-во Чебышева: пусть X – случ. величина, у кот есть M(X)=m и D(X)=a, тогда  >0 справедливо н-во P(|X-m|)  D(X)/² Док-во: P(X)  m/ - н-во Маркова. |X-m|; (X-m)²/²1;

P(|X-m|) = P((X-m)²/²1)  M((X-m)²/²) = 1/² M((X-m)²) = D/²; P(|X-m|) D(X)/².

Выборочная дисперсия D_b- среднее арифметическое квадрата отклонения наблюдаемого значения признака от их среднего значения Хв. Если все значения х₁+х₂+…+х_n выборки v n различны, то D_B=

Если значения признака х₁,х₂,…х_n имеют соответствующие частоты n₁,…n_k; n₁+…+n_k=n

D_B=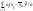

D=

D== ==

1°. Теорема Чебышева. Неравенство Чебышева позволяет доказать ряд важных теорем, объе-диненных одним общим названием "закон больших чисел". Основная из этих теорем принадлежит самому П.Л. Чебышеву.

1. Теорема 10.1. (теорема Чебышева). Пусть имеется бесконечная последовательность X₁, X₂, … независимых случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же постоянной:

Тогда, каково бы ни было положительное число , вероятность события

стремится к единице при

Доказательство. Положим,

.

В силу свойств математического ожидания имеем:

.

Далее, так как величины независимы, то

.

Сопоставив полученное неравенство с неравенством Чебышева:

,

будем иметь:

1. 

Это показывает, что с ростом n вероятность события стремится к 1.

Смысл теоремы Чебышева можно пояснить следующим примером. Пусть требуется измерить некоторую физическую величину m. В силу неизбежных ошибок результат измерения будет случай-ной величиной. Обозначим эту величину X; ее математическое ожидание будет совпадать с измеряе-мой величиной m, а дисперсия равна некоторой величине D (характеризующей точность измеритель-ного прибора). Произведем n независимых измерений и обозначим:

X₁ – результат первого измерения;

X₂ – результат второго измерения

и т.д. Совокупность величин X₁, X₂, …, X_n представляет собой систему n независимых случайных ве-личин, каждая из которых имеет тот же закон распределения, что и сама величина X. Среднее ариф-метическое этих величин тоже является, конечно, случайной величиной. Однако с увеличением n эта величина почти перестает быть случайной, она все более приближается к постоянной m. Точная количественная формулировка этой близости состоит в том, что событие становится как угодно достоверным при достаточно большом n.

Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если - сколь угодно малое поло­жительное число, то при соблюдении условий теоремы имеет место равенство . Доказательство. Обозначим через Х₁ дискретную случайную величину—число появлений события в первом испытании, через Х₂—во втором, ..., Х_n—в n-м испы­тании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероят­ностью р и 0 (событие не появилось) с вероятностью 1—р=q. Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины по­парно независимы и дисперсии их ограничены. Оба усло­вия выполняются. Действительно, попарная независимость величин X₁, Х₂, . . ., Х_n следует из того, что испытания независимы. Дисперсия любой величины X_i (i= 1, 2, . .., n) равна произведению pq, так как p+q=1,то произве­дение pq не превышает 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С =1/4. Применяя теорему Чебышева (частный случай) к рас­сматриваемым величинам, имеем Приняв во внимание, что математическое ожидание а каждой из величин X_i (т. е. математическое ожидание числа появлений события в одном испытании) равно ве­роятности р наступления события, получим Остается показать, что дробь (X₁+X₂+…X_n)/n равна относительной частоте т/п появлений события А в испытаниях. Действительно, каждая из величин X₁,X₂,…X_n при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма X₁+X₂+…+X_n равна числу m появления события в n испытаниях, а значит, Учитывая, это равенство, окончательно получим

. Итак, теорема Бернулли утверждает, что при относительная частота стремится по вероятности к p.

Х – биномин. Случайная величина с параметрами n и p

Если Х – случайная величина, явл-ся суммой большого числа независимых случайных величин, то случайная величина Х-МХ/ςх имеет распределение, близкое к стандартному нормальному, т.е.

Р{α≤X-MX/ςx≤β} = =Ф(β)-Ф(α) Х – число успехов в серии из n испытаний Х=Х1+Х2+…Хn

Где Хi=0, если в i-ом успеха не было, 1, если успех был. Р{α≤(X-np)/√npq≤β}= Ф(β)-Ф(α)

Р{np+α√npq≤x≤np+β√npq}