Метрология. Погрешности. Теоретические материалы. / Случайные погрешности

Случайные погрешности (СП).

СП – непредсказуемые ни по знаку, ни по величине погрешности.

Их можно обнаружить при повторных измерениях в виде разброса результата измерения. Описание СП проводят на основе теоретической вероятности и математической статистики.

В общем случае погрешность измерения состоит из

• систематических;

• случайных;

• промахов.

Систематические можно исключить. Случайные вызываются различными причинами не связанными между собой.

Случайные погрешности проявляются при повторных измерениях одной и той же величины в виде разброса показаний. Оценку СП проводят на основе обработки ряда наблюдений пользуясь теорией вероятности.

Полным описанием случайной величины является закон распределения. Он может быть задан в интегральной или дифференциальной форме.

Часто СП подчиняются закону Гауса(нормальный закон распределения).

- плотность распределения вероятности СП .

средне квадратичное отклонение.

Дифференциальный закон распределения: при увеличений  кривая становится более плоской.

Основные характеристики закона распределения – математическое ожидание m и дисперсия D.

Математическое ожидание ряда измерений будет истинное значение измеряемой величины. Систематическая погрешность смещает математическое ожидание.

Дисперсия ряда измерений характеризует степень рассеивания результатов отдельных измерений вокруг математического ожидания. Чем меньше дисперсия, тем точнее измерения. Т.к. D измеряется в квадрате измеряемой величины, то применяют: .

m и  определяют для большей группы измерений().

Если число измерений n<20, то определяют оценку m и .

a₁, a₂, a₃, …, a_n, где a_i – результаты отдельных измерений, n – число измерений.

, - средне арифметическое.

При

Обозначим

…

 - остаточные погрешности.

Оценка дисперсии ряда измерений:

Если , то,

- если отсутствует систематическая погрешность.

Если , то из ряда измерений вычитают систематическую погрешность и ряд называется исправным.

Из теории вероятности известно, что - Дисперсия средне арифметического в n-раз меньше дисперсии ряда измерений или

- средне квадратичное отклонение в меньше средне квадратичного отклонения ряда измерений.

Погрешность дискретности подчиняется равномерному закону распределения.

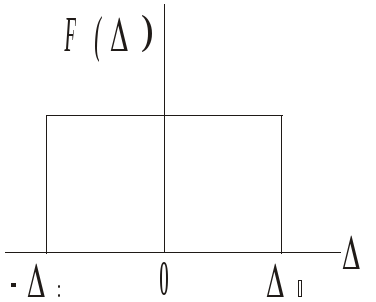
В качестве дифференциальных законов распределения берут прямые, площадь под которыми равна 1(вероятность достоверного события).

Законов распределения много.

Закон распределения для СП цифровых приборов.

Если известен закон распределения, то можно определить вероятность появления погрешности  не выходящей за пределы некоторой границы. Этот интервал называется доверительным, а его вероятность доверительной.

В метрологии доверительная вероятность: Р_д=0.9; 0.95

В теории надежности: Р_д=0.8.

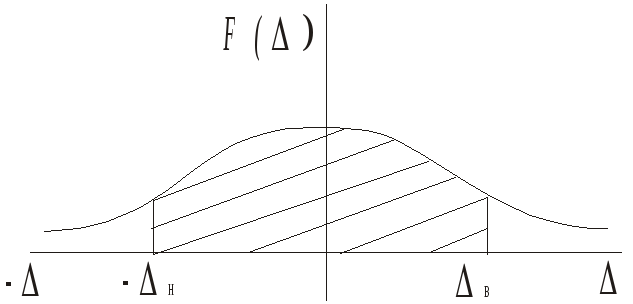
Р_д числено = площади ограничения кривой осью и вертикальными линиями соответствующих доверительному интервалу.

Для нормального закона распределения:

, где 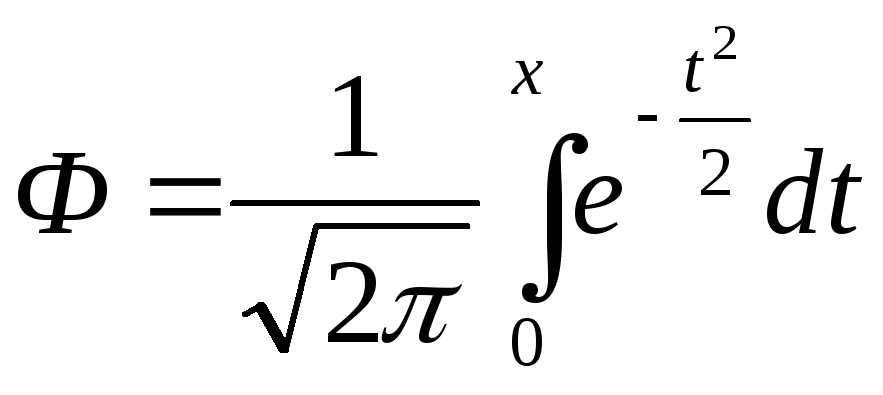- функция Лапласса.

Ф(0)=0, Ф(-х)=-Ф(х) - свойства функции Лапласса.

Часто нужно найти вероятность того, что СП по абсолютному величине меньше заданного положительного числа :

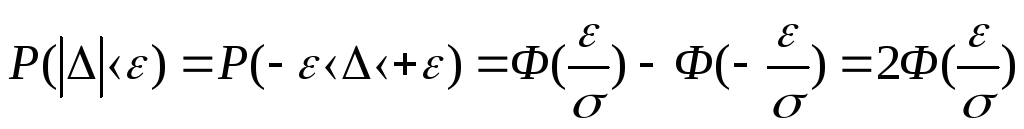
Найдем вероятность того, что

Правило трех .

Считают невозможным выход случайной ошибки за пределы трех , т.е. в 997 из 1000 случаев погрешность не превосходит трех 

Если погрешность больше трех , то результат измерения называется промахом, т.е. результат измерения содержит грубую погрешность, этот результат отбрасывается.

Если случайная ошибка распределена по нормальному закону и n<20, то истинное значение измеряемой величины находят с использованием закона Стьюдента.

.

Коэффициент t берут из таблицы распределения Стьюдента.

В результат измерения входит не исключаемая систематическая погрешность  и случайная погрешность.

Если , то пренебрегают  и считают, что погрешность только случайная.

Если , то пренебрегают СП, т.е. остается только систематическая погрешность.

Если , то границы погрешности находят по формуле из справочника.