1.Қандай да бір денеден алынған жылуды басқа денелердің күйін өзгертпей толығымен жұмысқа айналдыру мүмкін емес.

Шынында, егер де бір денеден алынатын жылу басқа денелерге берілмей, тек жұмыс істеуге ғана жұмсалатын болса, онда ол денелер адиабатты изоляцияланған болып шығады.Онда жылу алынған тұйық жүйеде энтропия кемиді, ал бұл ІІ бастамасы бойынша мүмкін емес.Алынған жылудың бір бөлігін ғана жұмысқа айналдыруға болады, ал қалған бөлігі басқа үшінші денелерге беріледі.

Осыдан шығатын салдар:қандай да периодты жұмыс істейтін жылу машинасы үш бөліктен құралады: қыздырғыш, жұмыс денесі және суытқыш.

Қыздырғыштан алынған жылу жұмыс денесіне беріледі.Онда циклдік үрдіс орындалады.Циклдік үрдіс кезінде сыртқы денелерге де жылу беріледі.Жұмыс қыздырғыштан алынған жылу есебінен істеледі, ал суытқышқа берілген жылу пайдасыз жаратылады.

Бұдан шығатын салдар: «екінші текті қозғалтқыш жасауға болмайды».

2.Тұйық жүйелерде өтетін қайтымсыз үрдістерде жүйенің энтропиясы ұлғаяды.

3.Нәтижесі, тек қыздырғыштан алынған жылуды оған эквивалентті жұмысқа түрлендіруде ғана болатын дөңгелек үрдістің өту мүмкін емес(Кельвин).

Жалпы, Кельвин принципіне жекелей тоқталсақ.

Жылуды механикалық жұмысқа айналдыру үшін оны ұлғая алатын денеге беру керек.Ең үлкен жұмыс изотермиялық үрдісте алынады, себебі ішкі энергия өзгермейді.Бұл жағдайда дененің атқаратын жұмысы сырттан алған жылу мөлшеріне тең.

Бірақ техникада жылудың механикалық жұмысқа түрленуінің осы сияқты бірлік үрдісі қызығушылық тудырмайды.Жылуды жұмысқа түрлендіретін нақты құрылғылар циклді түрде жұмыс істейді, яғни оларда болатын үрдістер периодты қайталанып отырады.Басқаша айтқанда, жүйе дөңгелек үрдіс жасауға тиісті.

Кельвин принципі:кейбір денеден тартып алынған жылуды механикалық жұмысқа түрлендіретін және сол кезде басқа денелерде ешқандай өзгерістерді тудырмайтын циклдік үрдісті жүргізу мүмкін емес.Сөйтіп, жылу қозғалтқышы жұмыс істеу үшін суытқыш қажет.

4.Нәтижесі, тек салқын денеден ыстық денеге жылудың берілуінде ғана болатын үрдістің өтуі мүмкін емес(Клаузиус).

5.Термодинамиканың маңызды салдарларының бірі:Тепе-теңдік үрдіске негізделген Карно машиналарының ПӘК-і бірдей және тек қана қыздырғыш пен суытқыштың температураларына тәуелді.Ол сондай температурада жұмыс істейтін, бірақ тепе-теңсіз үрдіске негізделген Карно машинасының ПӘК-інен әрқашанда артық болады».

1.3Қайтымды және қайтымсыз үрдістер.Карно циклі.

Термодинамиканың екінші бастамасы барлық үрдістерді: қайтымды және қайтымсыз деп екі санатқа бөледі.

Энергияның сақталу заңында (термодинамиканың бірінші бастамасында) оқшауланған жүйедегі үрдістер бағытына нұсқаулар болмайды, онда екінші бастамадағы сияқты осындай жүйедегі үрдістің кейбір бағыттары үшін қорытынды шығады.

Алайда, алдымен жүйедегі үрдістерді бөлудегі қайтымды және қайтымсыз үрдістерге тоқталу қажет, өйткені олардың анықтамай және олардың арасындағы айырмашылықты айқындамай екінші бастаманың мәнін түсіну мүмкін емес. Олардың әрбір параметрінің сатысында жағдай әбден айқындалатын үрдістер квазистатистикалық үрдістер деп аталады.

Қайтымды үрдіс деп- тепе-теңдік күйдегі жүйе өзінің алғашқы күйінен соңғы күйге өткенде параметрлері өзгеріп, үрдіс кері бағытта өте бастағанда, жүйе өзінің барлық күйі арқылы өтіп, қоршаған денелерде өзгеріс тудырмай бастпақы күйіне келуін айтады.

Физикада және қоршаған ортада кездесетін қайтымды үрдістерге келесілер жатады:

1.Барлық механикалық үрдістер, яғни толық және толықтай дерлік үйкеліс болмайтын механикалық қозғалыс. Оған мысалы өшпейтін маятник тербелісін, үйкеліссіз идеал сұйықтың қозғалысын, қатты ортада жұтылусыз дыбыс толқындарының таралуын, идеал қатты дене соққысын және тағы басқа үрдістерді жатқызуға болады.Аталған жағдайларда үрдіс тікелей сияқты қайтымды бағытта да оңай жүре алады.

2.Өшпейтін электромагниттік тербелістер.

Кедергі нөлге тең болатын контурда туған электромагниттік тербеліс белгісіз ұзақ уақыт бойы болады және тура және қайтымды үрдістерде электр кернеуінің және магнит өрісінің энергияға айналуы бақыланады. Бұл үрдістер қайтымды болып табылатыны белгілі, өйткені фаза ауысқанда үрдіс жүрген кезде айналада ешқандай жаңа өзгеріс болмайды.

3. Ортада электромагниттік толқынның жұтылусыз таралуы. Электромагниттік толқынның энергиясы жұтылғанда жылу пайда болады. Егер бұл құбылыс болмаса, онда толқынның таралу үрдісі қайтымды болып табылады, бұған тегіс жұтылмайтындай айнадан толқынның шағылу заңынан оңай көз жеткізуге болады. Шағылған сәуленің таралуы тікелей тура үрдіске жүгінуді білдіреді.

4. Термодинамикалық квазистатикалық үрдістер. Жоғарыда көрсетілген теңгерімсіз кеңею, диффузия және жылуөткізгіштік жойылған кезде, сонымен қатар үйкеліс жоқ болғанда квазистатикалық үрдістер үшін шарттарды пайдаланғанда барлық тепе – тең термодинамикалық үрдістер қайтымды болып табылады. Шынымен де, температураның, қысымның, көлемнің, концентрацияның т.б параметрлердің шамалы өзгерісі кезінде бағытының өзгерісі ешқандай рөл ойнамайды. Бірдей өлшемдегі жүйе өзгерісті тура және кері бағытта өткізе алады. Мысалы, температурасы дененің температурасынан болмашы ғана айырмашылығы бар денемен қатынасқа түскенде, соңғысы алады және жылуөткізгіштікті елемеуге болатын сонша аз жылу мөлшерін береді, өйткені барлық оқшауланған жүйедегі елеулі өзгерістерсіз үрдісті тура және кері бағытта жүргізуге болады.

Қарастырылған мысалдардан біз барлық қайтымды үрдістер қайтымды болып табылады деп қорытынды шығара аламыз, өйткені барлық жағдайда қозғалыста үйкеліс туады, барлық ортада электромагниттік толқынның жұтылуы жүреді, әрқашан жылуөткізгіштік құбылысы бақыланады және т.б. Сондықтан солай және квазистатикалық үрдістерді идеал қайтымды үрдіс деп есептеуге болады.

Ал егер үрдіс өзінің соңғы күйінен бастапқы күйге қайтқанда бұрынғы күйлердің бәрінен өте алмай, қоршаған ортаға өзгерістер тудырып жатса, ондай үрдісті қайтымсыз деп атайды.

Қайтымсыз үрдістер үрдістер айналу кезінде жүйенің барлық қасиеті өзгергенде оқшауланған жүйедегі күйдің өзгерісін білдіреді. Былайша айтқанда, оқшауланған жүйеде қайтымды қайтымсыз үрдісте тура үрдісте жүрмеген құбылыстар жүреді.

Қайтымсыздық тұрғысында Планк «әрбір қайтымсыз үрдіспен жүйе ешқандай жағдайда жоғалмайтын бірнеше қадам алға жасайды» деп айтқан болатын. Әрбір қайтымсыз үрдіс жүйеге қайта қалпына келмейтін өзгерістер енгізеді.

Қайтымсыз үрдістерге оқшауланған жүйедегі келесі қарапайым үрдістер жатады:

1.Температураның соңғы айырымындағы жылуөткізгіштік. Егер қызған денені суықпен байланысқа келтірсе, онда бірінші денеден екіншіге жылудың өтуі басталады және температураның тепе – теңдігі орындалғанша жалғасады. Үрдістің басында жүйе келесі шарттармен сипатталады: қызған дене температураға ие, суық дене температураға ие. Соңғы күйде екі температура да Т және температураға ие болады. Тура үрдіс «өздігінен» жүйеде жүреді және екі дененің қатынасуынан басқа ешқандай шарттарды талап етпейді деп айтылғанда оңай. Егер бұл үрдісті қайтаруға тырыссақ, яғни температурасы тең Т болатын қатынасқа түскен денелер күйден шығып, бір дене температураға қызатындай, ал екіншісі температураға салқындайтындай күйге жетеді, онда қайтымды үрдісте тура үрдісте болмаған қосымша шарттар қажет болатынына көз жеткізуге болады, өйткені қайтымды үрдіс өздігінен жүрмейді.

Біз тәжірибеден білеміз бірдей температурадағы екі денені біз қанша бақыласақ та, бір дене қызып, екіншісі суығанда өздігінен температураның айтарлықтай айырмашылығын байқай алмаймыз. Осылайша, оқшауланған жүйедегі жылуөткізгіштік – қайтымсыз үрдіс.

2.Үйкеліспен қозғалыс. Бір қатты дененің басқа дененің бетімен сырғанағанда немесе сұйықтардың қабаттарының арасындағы өзара сырғанауда үйкеліс пайда болады. Бұл үрдіс қайтымсыз, өйткені қозғалыстың механикалық энергиясы есебінен үйкеліс күшіне қарсы жұмыс жасалады. Осылайша қатынасатын беттер қызады. Үйкелісті жеңуге кеткен дененің энергиясы есебінен, денелердің салыстырмалы қозғалысының механикалық энергиясын тағы алу үшін кері үрдісте жүйеге жеткізуде қажет біраз жылу мөлшері бөлінді. Дегенмен алынған жылуды жұмысқа айналдыру мүмкін, бірақ кері үрдіс өздігінен жүрмейді, оны жүзеге асыру үшін тура үрдісте болмаған қосымша шарттар қажет. Сондықтан оқшауланған жүйедегі үйкелісті қозғалыс қайтымсыз үрдісті білдіреді.

3.Соңғы қысымдар айырымында газдардың таралуы. Джоуль мен Томсон тәжірибесінде бастапқыда ыдыста жасалған газ кранды ашқанда газдың бастапқы қысымынан көп аз қысым бар кеңістікке немесе «бос кеңістікке» таралады. Мұндай құбылысты қайтымсыз деп есептеуге болады, өйткені үрдістің айналымы кезінде тура үрдісте болмаған манипуляцияны жүргізуге тура келеді. Газ өздігінен бір ыдыстан екіншісіне ақты, және қысым теңескен соң тоқтады. Кері бағытта үрдіс жүрмейді, яғни газ өздігінен бірінші ыдысқа бұрынғы қысымның бөлінуі түрінде қайтпайды. Дегенмен жасанды түрде, арнайы құрылғылардың көмегімен газға қатысты бұл үрдісті қайтаруға болады, бірақ оларды пайдалану жүйеге енгізуге тура келетін тура үрдіске қатыспаған қосымша шарттарды қолдану болып табылады. Сондықтан, Джоуль – Томсон эффектісі оқшауланған жүйедегі қайтымсыз үрдіс болып табылады.

4.Диффузия. Жүйенің жеке бөлігінде заттың концентрациясының айырмашылығы болатын жүйеде жүретін үрдіс. Егер ыдыстағы ерітіндінің бетіне таза еріткіштің біраз бөлігін мұқият құйса, онда концентрация теңескенге дейін жалғасатын диффузияның ерікті үрдісі басталады. Ерітінді бастапқы күйде концентрацияға ие болды, онда еріткіштегідей с=0 болады. Үрдістің соңында орташа жалпы концентрациясы алынады. Бұл үрдіс қайтымсыз болып табылады, өйткені айналу кезінде тура үрдісте қатыспаған әдіс – тәсілдерді қолдануға тура келеді. Шынымен де, араласқан заттардың өз еркімен бөлінуі жүрмейді, дегенмен жасанды бөліну жүргізуге болатыны бізге белгілі, және бұл үшін көптеген технологиялық үрдістерде қолдануға болады, мысалы қоспаларды бөлуде, изотоптарды бөлуде, ерітіндіден заттарды бөлуде және т.б. Көрсетілген мысалдармен қатар, тағы басқа көптеген қайтымсыз үрдістерді жүргізуге болады. Мұнда өткізгіштегі кедергімен электр тогының жүруін, жұтылатын ортада электромагниттік толқынның таралуын, тез жүретін химиялық үрдістерді (мысалы, жану, жарылу), сонымен қатар радиоактивті ыдырауды жатқызуға болады. Көрсетілген үрдістердің комбинациясы бар түрлі күрделі үрдістер де қайтымсыз болып табылады.

Бұдан басқа, қайтымсыз үрдістер бізді қоршаған әлемде таралған шынайы үрдістер санына жатады. Макроәлемдегі көптеген шынайы үрдістер қайтымсыз, және егер үйкелісті, жылуөткізгіштікті ескермеген жағдайларда ғана бұл үрдіс қайтымдыға жақын болады.

Табиғатта болып жатқан көптеген үрдістерге аса қатты мән бермейміз.Дегенмен, әрбір үрдістің, әрбір заттың «Неге? Не себепті?» деген сұрақтарды туындататыны анық.

Термодинамиканың мәнін ашатын қайтымды және қайтымсыз үрдістер аса терең мәнге ие.

Енді қайтымды және қайтымсыз үрдістердегі энтропияны қарастырайық.

Жоғарыда айтқанымыздай, энтропия ұғымы үш салада: термодинамика, статистикалық физика және киберентикада қолданылады.Энтропияның классикалақы термодинамикадағы анықтамасы:

(9)

Жүйе бір тепе-теңдік күйден екінші тепе-тең күйге көшсе, оны мына өрнек арқылы жазуымызға болады (10):

(10)

Ал кері қайтып келсе, оны мына формула арқылы көрсетуімізге болады(11):

(11)

Бірінші үрдіс l₁ болса, екіншісі l₂ болсын.Кері бағытта өткізгенде тепе-тең күйлерден өтетін немесе бұрынғы өткен күйлерден қайта өткізу мүмкін боса, мұндай үрдіс қайтымды деп аталады.Осы шарт орындалса, яғни l₁-қайтымды үрдіс болып,кері қайтқанда жүйе l₂ үрдіспен бұрынғы өткен күйлерден өтетін болса, онда L=l₁+l₂ қайтымды цикл болады, ал энтропия өзгермейді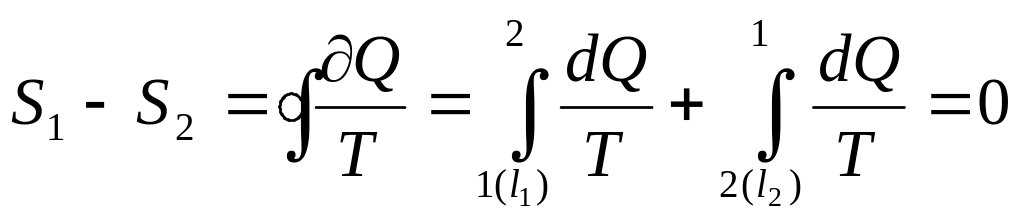(12):

(12)

Бұдан табатынымызды мына теңдеу арқылы жазып көрсетеміз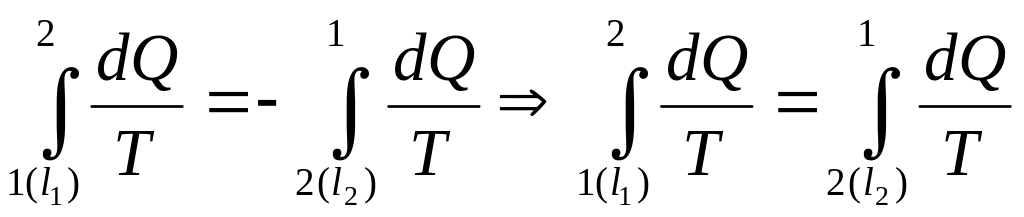(13):

(13)

l₁ және l₂ үрдістері қайтымды болып, басқа жағынан бұлар әр түрлі болғандықтан, (13) теңдіктен көретініміз: бір күйден екіншісіне өткен кезде, өту жолы қандай болса да, интегралы бірдей мәнге ие болады.Демек, бұл шама жүйе күйіне ғана тәуелді.

Энтропияның физикалық мағынасын статистикалық физика ашады.Энтропияны өзгертетін бір фактор- жылу алмасу: болғанда, , яғни, жылу жұтқанда, энтропия артады, ал болғанда, - жылуды маңайдағы ортаға бергенде, энтропия азаяды.

Барлығымыз білетініміздей, «энтропия» ұғымын К.Клаузиус енгізген болатын.ЭН(ергия)ТРОПЕ( түрлену) мағынасын береді.Энтропия белгілі бір тұрақтылыққа дейін дәлдікпен анықталған(14):

(14)

Аддитивті тұрақтыны Нернст теоремасының көмегімен анықтайды.Жүйеге жылу бергенде жүйенің ішіндегі бөлшектердің қозғалысындағы ретісзідігі және ішкі құрылымның тәртіпсіздігі күшейеді, мысалы: кристалды қыздырғанда, жылулық тербеліс амплитудасы күшейіп, ақырында белгілі бір температурада кристалдың құрылымы бұзылады,- атомдар тербелісіне атомдардың бір нүктеден екіншісіне секірулері қосылады.Сөйтіп, энтропия өседі.

Сонымен, энтропия- жүйенің ішкі құрылымындағы ретсіздігінің және құрамындағы бөлшектердің қозғалысындағы реттелмегендігінің өлшемі болып табылады.Осы тұрғыдан келгенде, энтропияның термодинамикадағы және статистикалық физикадағы анықтмалары ұщтасады.

Механикалық үрдісті тура және кері бағытта өткізуіміз мүмкін.Мұндай үрдісті қайтымды деп атайды.

Ал, термодинамикадағы тұйық үрдісті бірдей теңбе-тең күйлер арқылы тура және кері бағытта өткізуіміз мүмкін болса, жаңа айтқанымыздай, бұл үрдіс қайтымды деп аталады,ал мүмкін болмаса, қайтымсыз деп аталады.

Ол жөнінде « тура бағытта жүреді, кері бағытта жүрмейді» деп анықтама берген дұрыс емес.Қайтымсыз үрдісті тура және кері бағытта өткізуіміз мүмкін, тек кері бағыттағысы өздігінен өте алмайды.

Мысалы: денені қыздыру не суыту үрдістерінің біреуі өздігінен өтсе, екіншісі, яғни кері үрдіс тоңазытқышта немесе пеште өтеді.

Қайтымды үрдіс квазистатиклық үрдіс болады және диссипативтік эффектілермен қабаттаса жүрмейді.Мысалы, турбуленттік, үйкеліс немесе электр кедергісі сияқты қайтымсыз ұрдістерге ,яғни тұтқыр сұйықтың турбулентті араласуы, электр зарядтың кедергіден өтуі, газдың вакуумге еркңн таралуы, екі газдың араласуы сияқты үрдістер және серпімсіз деформацияда энергия шығыны, поляризациялану және магниттелу кезіндегі үрдістер жатады.Демек, ол өткеннен кейін маңайдағы денелердің күйінде өзгеріс болуы мүмкін,Үрдісті жүргізіп, одан кейін жүйені кері бағытта сол жолмен алып келгенде, жанындағы ортада өзгерістер болса, онда үрдіс қайтымсыз деп аталады.

Энтропияның өсуі қайтымсыз үрдіспен байланысты.Жүйенің және онымен әсерлескен барлық денелердің энтропиясы өседі.

Барлық табиғи үрдістер қайтымсыз, алайда жуықтап механика мен электрмагнит құбылыстарын қайтымды деп есептеуге болады.Статистикалық физикада газдың изотермиялық ұлғаюы қайтымды үрдіске жатады.Сонымен, қайтымсыз үрдісте энтропия тек жылу беру арқылы ғана емес, сонымен бірге басқа да себептермен өзгереді(15):

(15)

Релаксация нәтижесінде біртесіздіктер жойылады.Бірінші мүшесі оң да теріс болуы мүмкін, екінші мүшесі оң болады.Сондықтан қайтымсыз үрдіс үшін энтропияны былай жазамыз(16):

(16)

Сонымен, қайтымсыз үрдістер кезінде энтропия үнемі өседі.Бұл қорытынды физикада маңызды орын алады.Бұл қайтымсыз үрдістердің маңызды белгісі.Бұл қорытынды ХІХ ғасырда К.Клаузиустың «Әлемнің жылулық ақыры» жөніндегі аты шулы гипотезасына негіз болды.Бұл гипотезасына сәйкес Әлемде энтропия үнемі өсетіндігі салдарынан келешекте энтропия барлық нүктелерде максимумға жетеді және бірыңғайлылық орнайды.Жылу барлық орындарға бірдей таралып, жаңа құрылымдардың пайда болуына түрткі болатын температура градиенті сақталмайды.Бұл гипотеза әлі де толық дәлелденбеген.Оған қарсы шығып, табанды күрескендердің бірі-Больцман болатын.Оның әйгілі Н теоремасы жоғарыда аталған үрдістерген парапар үрдісті сипаттайды.Тепе-тең үрдісте Больцманның Н-функциясы минимумға келеді және осы функция энтропияға пропорцианал болатын шама.

Физикада материялардың қасиеттерін зерттеп, түсіну үшін оларды екі тұрғыдан қарастырады деуге болады.Физикалық құбылыстардың мән-мағынасын тар және кең мағынада ашып көрсетуге болады.

Сонымен қатар табиғатта кездеспейтін, адам өз ойынан ойлап шығарған идеал ұғымымен және осыған қарама-қарсы нақтылық сипаттамаларына ие

«Идеал» ұғымы- физикалық құбылыстардың мағынасын түсінуде , физикалық мәндерді және есептерді шешуде қолданған кезде жеңілірек болады.Қарапайым мысалы ретінде «идеал газды» алуымызға болады.Идеал газдың құрамы, ондағы молекулалардың орналасуы мен қозғалысы, жылдамдығы және тағы да басқа физикалық сипаттамаларын есептеп шығару бізге жеңіл болады.

Сол сияқты термодинамика саласында қолданып келе жатқан идеал түсініктердің бірі –«Карно циклі» болып табылады.

Карно циклін тар мағынада ашып айтатын болсақ, ол - идеал термодинамикалық цикл. Ал кең мағынада, екі адиабаталық және екі изотермиялық үрдістен тұратын айналмалы қайтымды үрдіс.

Карно үрдісінде термодинамикалық жүйе механикалық жұмыс жасайды және температурасы тұрақты, бірақ сан мәні жағынан айырмашылығы бар екі резервуар арасында жылу алмасу жүзеге асады. Температурасы жоғары резервуар қыздырғыш деп аталады, ал төменгі температурасы тоңазытқыш деп аталады.

«Карно циклі» атауын атақты француз ғалымы Сади Карноның құрметіне қойған. Бұл туралы алғаш рет 1824 жылы «Машиналар және отты қозғалтатын күш туралы» еңбегінде сипаттама берген болатын.

Қайтымды үрдістер шексіз өте аз жылдамдықта жүзеге асатындықтан, Карно цикліндегі жылу машиналарының қуаты нөлге тең болады.Ал нақты жылу машиналарының қуаты ешқашан 0-ге тең болмайды, сол себепті нақты үрдістер идеал қайтымды Карно үрдісіне шамамен жуықтап жақындайды.

Карно цикліндегі жылу машиналары басқа жылу қозғалтқыштарына қарағанда максималды мүмкін болатын ПӘК-і мөлшерінде жылуды жұмысқа айналдырады.Олардың жұмыс цикліндегі максималды және минималды температуралары Карно цикліндегі қыздырғыш пен тоңазытқыштың температураларына сәйкес келеді. Карноның зерттеулерінің терең мағынасын түсінуге тырысқан Клаузиус энтропия ұғымын ашқан болатын.

Карно өзінің зерттеулерінде « Егер екі денелердің,яғни қыздырғыш пен тоңазытқыштың арасында қайтымды термодинамикалық үрдіс болатын болса, онда қыздырғыштан Q₁ жылу мөлшерін алып, оның белгілі бір бөлігін Q₂ тоңазытқышқа беру арқылы жұмыс істейтін жылу машиналары құрастырылған еді.Сонымен қатар, берілген жылу мөлшері мен алынған жылу мөлшері қыздырғыштың және тоңазытқыштың температурасына байланысты екенін дәлелдеген болатын.

Яғни, бұл дәлілдемені төмендегі қатынас арқылы көрсетуге болады(17):

ǀQ₁ǀ:ǀQ₂ǀ=ǀT₁ǀ:ǀT₂ǀ (17)

Бұл қатынас кез-келген идеал жылу машинасы үшін нақты болып табылады.

Жазылған қатынасты мына түрде жазуымызға болады:

(18)

«-» таңбасы жұмыс газынан жылу мөлшері алынып жатқанын көрсетеді.Осыдан шығатын теңдік:

(19)

Сақталу заңына ұқсайтын теңдеу аламыз.Карно цикліндегі жұмыс қыздырғыштан «алынған» шама тоңазытқышқа «берілген» шамаға тең болады.

Сади Карно зерттеулер жүргізгенде сутегі элементінің моделін қолданған.Бұл үлгі арқылы жылу сұйықтығының гипотетикалық сақталуын сипаттайтын қатынас түрін алуымызға мүмкіндік береді.

Егер ǀQ₁ǀ=ǀQ₂ǀ қатынасы орындалса, онда сутегі үлгісі жарамды болар еді.Яғни, жылу сақталып, ал жұмыс болса, өте жоғарғы температурадан өте төменгі температураға өту арқылы жүзеге асар еді.

Егер де температура биіктіктің аналогы болса, онда машина жасайтын жұмыс температура айырмасына пропорцианал болар еді.Алайда, зерттеулер барысында байқағанымыздай, қайтымды үрдіс кезінде дененің бойындағы жылу мөлшері тұрақты болмайды.Сондықтан, үрдістің бойындағы жылуды температура шамасына «бөлсек», онда қайтымды үрдіс кезінде сақталатын физикалық шаманы аламыз.

Карно циклін қолдана отырып, газдың күйін сипаттайтын энергия, қысым және температура сияқты параметрлерге ұқсайтын қандай да бір S шамасының бар екенін Клаузиус тұжырымдаған болатын.

Газға аздаған жылу берген кезде ондағы S шамасы өсетіндігін байқалқан.Осы шаманы Клаузиус энтропия деп атаған.

Саади Карноның зерттеулерін пайдалана отырып, Клаузиус жылу мен температура параметрлерінің арасындағы байланысты ашып, оған энтропия деп атау берген еді.

Жалпы, Карно цикліндегі жылу машинасының сипаттамасына тоқталсақ.

Карно цикліндегі машиналар температуралары әр түрлі қыздырғыш пен тоңазытқыш резервуарларынан тұрады.

Яғни, сипаттама беру үшін қыздырғыштың температурасын деп, ал тоңазытқыштың температурасын деп аламыз.Бұл резервуарлардан басқа бізде жұмыс денесі болады.

Карно циклі 4 деңгейден тұрады.Ол деңгейлердің екеуі тұрақты температурада( изотермиялық), ал қалған екеуі тұрақты энтропия кезінде жүзеге асады.Сол себепті Карно циклін координата жүйесінде осы екі тұрақтылар арқылы көрсету ыңғайлы болып табылады.

1.Изотермиялық ұлғаю(суреттегі A→Б үрдісі). Үрдіс басында жұмыс денесі температурасына, яғни қыздырғыштың температурасына ие болады.Одан кейін қыздырғышпен жалғап, тұрақты температурада жылу мөлшерін береді.Бұл кезде жұмыс денесінің көлемі ұлғайып, жұмыс жасайды және оның энтропиясы өседі.

2.Адиабаталық ұлғаю(суреттегі Б→В үрдісі).Жұмыс денесі қыздырғыштан ажыратылып, қоршаған ортада жылу алмасусыз ұлғаюын жалғастырады.Бұл кезде дене температурасы тоңазытқыштың температурасына дейін төмендеп , дене жұмыс жасайды.Ал энтропия тұрақты болып қалады.

3.Изотермиялық сығылу (суреттегі В→Г үрдісі ). температурасына ие жұмыс денесін тоңазытқышқа жалғап, сыртқы күштердің әсерінен изотермиялық түрде сығыла бастайды.Бұл кезде тоңазытқышқа жылу мөлшерін береді.Дене жұмыс жасайды және оның энтропиясы төмендей бастайды.

4. Адиабаталық сығылу (суреттегі Г→А үрдісі ). Жұмыс денесі тоңазытқыштан ажыратылып, жылуалмасусыз, сыртқы күштердің әсерінен қораған ортада сығыла бастайды.Бұл кезде дененің температурасы қыздырғыштың температурасына дейін ұлғайып, дене жұмыс жасайды және оның энтропиясы тұрақты болып қалады, ол 1-суретте көрсетілген

Сурет 1 Координатадағы Карно циклі T- S

Cонымен қатар, Карноның цикліндегі жылу машинасының жұмыс істеу принципін тереңірек қарастырайық.(2 суретте көрсетілген)

2- сурет- Карно циклі.

Карноның қайтымды машинасы циклдің идеал сызбасын көрсетеді, және оның іс – әрекеті келесідей болады. Поршенді цилиндрде идеал газдың бір молі орналасқан. Цилиндр және поршень жылу өткізбейтін материалдан жасалған, ал цилиндрдің түбіне жылуды өте жақсы өткізгіш орналастырылған. Поршень үйкеліссіз цилиндрдің қабырғасы бойымен сырғанауы мүмкін. Осы құрылғының көмегімен қайтымды үрдісті жүзеге асыра отырып цилиндрдегі газ күйінің өзгерісінің циклін жүргіземіз, және машина жұмысы мен пайдалы әсер коэфицентін табамыз. Жұмысты табуға байланысты ең тиімді үрдіс изотермиялық және адиабаталық үрдіс болып табылады, өйткені біріншіден оларды барлық берілген жылу толығымен жұмысқа айналады, екіншіден жұмыс газдың ішкі энергиясының жоғалуының есебінен жасалады. Газ бастапқыда температураға ие болсын, оның көлемі мен қысымы және . Цилиндрді үлкен өлшемді температураға ие шартты түрде қыздырғыш немес жылу көзі деп аталатын табақшаға қоямыз, және біртіндеп поршеннен жүкті шеше отырып газды тұрақты =const температурада көлемге дейін қайтымды таратамыз. Үрдіс изотермомен көрсетілген (1-2). Мұнда изотермиялық үрдісте қыздырғыштан алынған жылу осы үрдістегі жұмысқа тең деп есептелген (20):

(20)

2-ші күйге жеткен соң қыздырғышты алып тастаймыз, цилиндрдің түбіне жылу өткізейтін материалдан пластиананы орналастырамыз, және поршендегі жүкті азайта отырып, газды адиабаталық таралуға ұшыратамыз (Q=0). Осыдан оның температурасы көлемге жеткенше - ға дейін төмендейді. Осыдан кейін жылу өткізбейтін пластинаны алып тастап, цилиндрді осы сәттегі газ температурасына тең болатын температураға ие үлкен өлшемді дененің бетіне қоямыз. Бұл біраз суық дене, шарт бйынша тоңазытқыш деп атаймыз. Енді изотермиялық және қайтымды түрде көлемін -тен - ке кішірейте отырып газды сығамыз, оның шамасын төменде есептейміз. Осыдан газ тоңазытқышқа газбен жасалған жұмысқа тең болатын жылу береді, бұны мына теңдік арқылы көрсетуге болады(21):

(21)

көлемге жеткен соң тоңазытқышты алып тастаймыз және қайтадан цилиндр түбіне жылуөткізбейтін пластинаны төсейміз. Қайтымды адиабаталық үрдісті (Q=0) жүргізе отырып газды сығуды жалғастырамыз. Осыдан газ температурасы жоғарылайды, және газ температураға қайта қызғанда біз сығуды тоқтатамыз.

Егер көлем дұрыс таңдалған болса, онда газ температураға ие бола отырып бастапқы көлемге қайта ие болады және операцияның бір циклін өтіп бастапқы 1 – ші күйге өтеді.

Енді Карно машинасының жұмыс барысында жүйеге енгізетін өзгерістеріне байланысты әрекетін бағалаймыз. Бір циклде жылудың біраз бөлігі қыздырғыштан алынды және жылудың басқа бөлігі тоңазытқышқа берілді, < , жылу бөлігі - газдың пайдалы әсер коэфицентіне кеткені айқын, яғни

. (22)

Карно машинасының пайдалы әсер коэфиценті басқа жылу машиналарындағыдай мынадай қатынаспен өрнектелуі мүмкін:

, (23)

болғанда, және осыдан

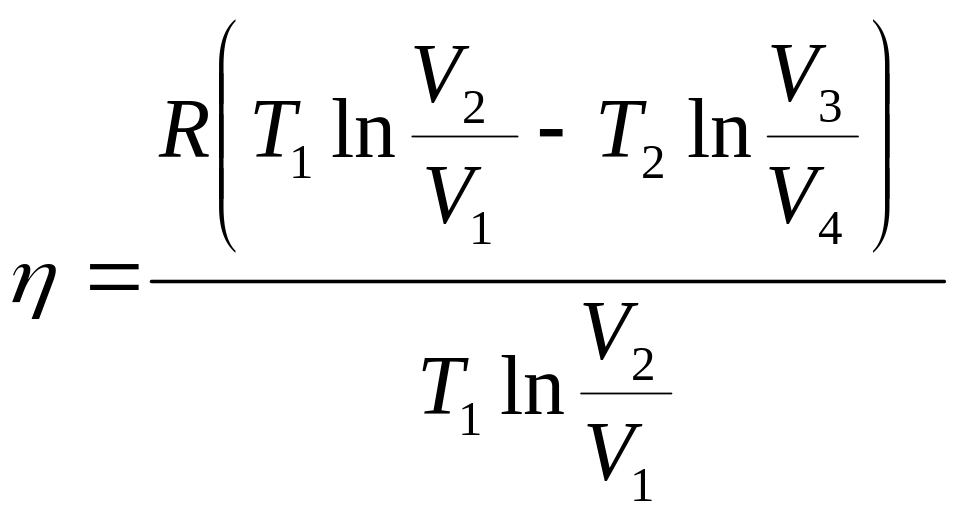. (24)

және көлемдерінің байланысын анықтаймыз. Бұл үшін адиабаталық үрдісте температураны көлеммен байланыстыратын формуланы пайдаланамыз. Адиабаталық үрдіс үшін (2-3) ;

, (25)

Онад адиабатадағы сияқты (4-1)

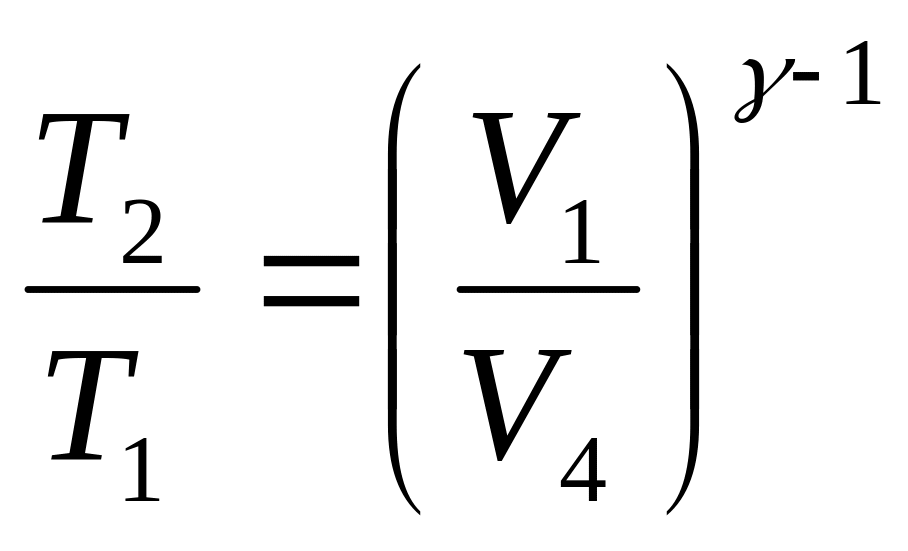. (26)

(20) және (21) теңдулерді салыстыра отырып, табамыз

. (27)

Соңғы пропорциядан шығатыны

. (28)

Сондықтан Карно машинасының пайдалы әсер коэффициенті

(29)

Осы өрнектен ең алдымен практикалық салдары шығады. Изотермиялық және адиабаталық үрдісте пайдалы жұмысты алу тұрғысынан ең тиімді пайдаланылатын идеалды қайтымды машина үшін де пайдалы әсер коэффициенті 100% - ға жетпейді.

Соңында тоңазытқыш температурасы абсолют нөлге тең болғанда пайдалы әсер коэффициенті бірлікке айналады,бірақ бұл жағдай қол жетімсіз. Өйткені, , онда Карноның барлық идеал машиналары үшін .

Жұмыс істейтін дене, яғни газ циклдің аяқталуына қарай бастапқы күйге өтетінін байқаймыз, және ішкі энергиясының өзгермегенін білдіреді; сондықтан қыздырғыштан алынған жылу , - көлемі жұмысқа айналды, ал қалған қыздырғыштан алынған тоңазытқышқа беріледі. Сәйкесінше, газ соңында жылуды алған да жоқ, берген де жоқ, ол тек қыздырғыш пен тоңазытқыш арасындағы байланыстырушы дене болып табылады. Қарастырылатын Карно машинасы кері цикл бойынша жұмыс істейтін кері машинадан айырмашылығы қайтымды машина деп аталады. Соңғысының біріншіден айырмашылығы операцияның циклінің айналуынан тұрады (бірақ поршень жүрісінің бағытының өзгерісінде емес).

Карноның қайтымды машинасының кері әрекетін қысқаша қарастырамыз. Онда операция циклін келесі қайтымды үрдістерге бөлуге болады (3 суретте көрсетілген):

3- сурет.Карноның кері циклы.

-Адиабата бойынша (1-2) көлемнің - дің -ге өзгерісінде -ден -ге газдың салқындауымен газдың адиабаталық таралуы;

-Изотерма бойынша (2-3) көлемнің - ден - ке өзгерісінде тұрақты температурада изотермиялық таралуы;

-Адиабата бойынша (3-4) көлемнің - тен - ке азаюы кезінде -ден -ге қыздыру жүргендегі адиабаталық сығылу;

-Көлемнің -тен бастапқы -ге өзгеруінде температурада изотермиялық сығылу (4-1).

-Газдың изотермиялық таралуы кезінде (2-3) температурада суық денеден толық жұмысқа айналатын жылу алынады; керісінше, изотермиялық сығылу кезінде (4-1) жолы бойынша жылу температурасы көбірек қыздырылған денеге беріледі ( әрине, > ), және газбен ішкі жұмыс жасалады.

Осындай машинаның жұмысында цикл бойынша келесілер алынатыны белгілі: - - ге тең болатын және қисықсызықты фигура ауданымен салынған (1,2,3,4) газбен жасалған сығылу жұмысы жылуға айналады және жылуы суық денеден жылыраққа өтті.

Қызған денеге берілген жылу мөлшері суық денеден алынған және сығылу жұмысынан алынған - жылудан құралатыны белгілі.

Қайтымды машина пайдалы жұмыс бермейді, өйткені цикл бойынша жасалған жұмыс газдың өзінің жұмысынан көп, бірақ бұл машинаның өзі негізінде пайдалы болып табылады, себебі оның көмегімен суық денеден жылуды алып және оны біртіндеп салқындатуға болады. Карно қайтымды машинасы тиімді тоңазытқыш машина болып табылады. Біз оның пайдалы әсер коэфицентін табуға тоқталмаймыз, өйткені бізге белгілідей тура машинадағыдай мына формула бойынша табылуы мүмкін:

. (30)

Бұл жағдайда да газ байланыстырушы дене болып табылады және бір циклде бастапқы күйге өтеді; нәтижесінде оның ішкі энергиясы өзгеріссіз қалатынын байқаймыз. Соңында қыздырғыш пен салқындатқыш арасында бірі тура, ал екіншісі қайтымды болып табылатын екі Карноның қайтымды машиналары жұмыс істейтін елестетеміз. Олардың бірлескен жұмысында оқшауланған жүйеде еш өзгеріс болмайтыны белгілі. Бірінші машинадан алынған - пайдалы жұмысты толығымен екінші машинада газды сығуға жұмсай аламыз; нәтижесінде қыздырғышта да, тоңазытқышта да еш өзгеріс болмайды және екі газ мөлшері де өзгеріссіз алады.

Соңғы дәлелдемелер бойынша Карно циклі бойынша жұмыс жасайтын жылу машинасының ПӘК-і тек қыздырғыш пен тоңазытқыштың температурасына ғана тәуелді екенін дәлелдедік. Жылу машинасының ПӘК-і осы құрылғыға да,оның түріне де және жұмыс денесінің қасиетіне де байланысты емес.Бұл нәтиже Карноның бірінші теоремасы болып табылады.

(31)

Егер тоңазытқыштың температурасы абсолют 0-ге тең болса ғана, құрылғының ПӘК-і 100 % бола алады.Бұл мүмкін емес.Дегенменде, табиғатта абсолют нөлге жету еместігін термодинамиканың үшінші бастамасы анықтаған.Бірақ, Карно циклінде бұның себебін ғалымдардың бірі циклдің түріне байлансыты десе, енді бірі Карно циклінің екі адибаталық және изотермиялық үрдістердің жиынтығынан пайда болатындығымен байланыстырады.

Сөл себепті, кез-келген жылу машинасының ПӘК-і Карноның қайтымды машинасының ПӘк-нен асып түсе алмайды.Бұл тұжырымдама-Карноның екінші теоремасы.

(32)

Осы теореманың арқасында кез-келген жылу машинасының ПӘК-нің шегі анықталған және құрылғының нақты ПӘК-нің максималды мәннен қаншалықты ауытқығанын бағалауға мүмкіндік береді.

Сондықтан, Карно теоремасы — жылу қозғалтқыштарының пайдалы әрекет коэффициенті туралы теорема.

1.4 Температураның термодинамикалық шкаласы

Термодинамика бөлімінің маңызды параметрлерінің бірі температура болып табылады. Температура- жылу құбылыстарымен тығыз байланысты негізгі физикалық шама.

Температура туралы түсінік ғылымда бірнеше жүздеген жылдар бұрын пайда болған.Ертедегі ғалымдар жылудың күйі туралы жылуды немесе суықты нақты сезіну арқылы тұжырымдар жасағанмен, бұл тұжырымдар субъективті, дәл және анық емес еді. Дене әр түрлі дәрежеде қызу қасиетіне ие бола алады.Бұл қасиетті температура деп атайды.

XVIII ғасырда құрастырылған аспаптардың барлығы су, сынап және спирт бағаналары ұзындығын қолданa отырып, температураны өлшеген болатын.

Екі бірдей термометрді құрастырып, олардың көрсеткіштері әрқашан бірдей болатындай жағдай жасауға болатын еді.Бірақ та, термометрлер температураны өлшеген кезде белгілі бір шекті интервалы болды.Термометрдегі сұйықтықтар біресе қайнап, біресе қатып қалатын.Сол себепті, төменгі және жоғарғы температураларды өлшеу мүмкін емес еді.Сонымен қатар, температура шкаласының әр түрлі орнындағы градустар арақатынасын білген де пайдалы.

Осындай мәселелердің туындауынан жаңа термометрлер, өлшеу әдістері және шкала түрлері дүниеге келген.

Алайда, жаңадан қадам бастап келе жатқан термометрия саласының алдында мынадай екі мәселе туындаған еді.

Біріншісі, термометр шкаласының нүктелері сәйкес келетін қандай да бір шартты тағайындау керек.Көбінесе, шкаланың басына және санау ретіне қатты назар аударылды.

Екіншісі, белгілі бір термометрге тәуелді болмайтын градус ұғымына анықтама беру керек еді және ол Жердің кез-келген нүктесінде және кез-келген уақытта қолданатындай шкала құрастыруды жүзеге асыруы тиіс болатын.

Тұрмыста және техникада жиі қолданылатын Цельсий температура шкаласының басы мен соңғы градус мәндері белгіленіп, шкаланың аралық интервалдары бірдей бөлікке бөлінген.Дегенменде, сынап бағанасы бір градусқа көтерілген кезде температурасы өлшеніп отырған дененің бойында қандай өзгерістер болатындығын анықтау қажет еді.

Дененің температурасы жоғарылаған кезде дененің энергиясы да ұлғаяды.Осы шаманың дене массасына қатынасы арқылы өрнектелетін физикалық шаманы меншікті жылусыйымдылық деп атайды.

Алайда, тәжірибеден көргеніміздей, әр түрлі дененің жылусыйымдылығы да әр түрлі болады және шкаланың әрбір орнында дененің температурасын 1°-қа жоғарылату үшін жұмсалатын жылу мөлшері де әр түрлі болып өзгереді.Сондықтан, бұл мақсатты орындау үшін қарапайым заттар жарамсыз болды.

Жарамды заттардың қатарына идеал газды жатқызуға болады.Гей-Люссак заңына сәйкес көлем тұрақты болып,оның қысымы температура шамасына сызықты түрде өзгереді.Нақты газдар өзінің қасиеттері мен параметрлерінің сипаттамасына қарай идеал газға өте жақын келеді.

Әрине, кез-келген температурада және қысымда бұл әдісті қолдануға болмайды.Өйткені, қайсыбір уақытта нақты газда идеал газ болуын тоқтатады.Молекулалық физикадан білетініміздей, газ қысымы температураға тәуелді:температура жоғарылаған сайын газ қысымы ыдыстың қабырғасына көбірек түседі де, ал температура төмендесе, қысым кемиді.Молекулалық теория тұрғысынан қарағанда, молекулалардың температурасы артқан сайын олар шапшаң қозғалып,ыдыс қабырғасына қатты соғылады.

Егер газы(аргон, неон, сутек немесе гелий) бар баллонды манометрмен жалғайтын болсақ, онда газ термометрді деп аталатын құралды алуға болады.Температурасы өлшенетін денемен баллонды жылулық байланысқа келтіреді.Біраз уақыттан кейін дене мен баллондағы газдың температуралары теңеседі де, манометрдің көрсетуі бойынша дененің температурасын білуге болады.

Газ термометрі- өте күрделі құрылғы.Оны негізінен, неғұрлым қарапайым, екінші реттік термометрлерді градуирлеуге пайдаланады.Сонымен қатар, бұндай газ термометрлері көптеген зертханалық жұмыстарды және тәжірибелерді орындау кезінде зертханалық орындарда қолданылады.

Егер температура физикалық шама болатын болса,онда термометрдің сұйықтығының материалына тәуелсіз болатын өлшеудің қандай да бір әдісін ойлап табу керек еді. Термодинамика ғылымы дүниеге келген соң ғана осы сұрақтың жауабын Карно цикліне сүйене отырып, 1848 жылы Клаузиус тапқан болатын.

Ғалым Кельвиннің температура туралы теорияларынан кейін мынадай тәжірибелік мәселе туындады: нақты өлшеулерге жарайтын термометрдің эталон шкаласы қандай қағида бойынша құрастырылуы керек?

Көптеген жылдар бойы температура шкаласы үшін екі нүкте таңдап алынған: мұздың қату температурасы мен судың қайнау температурасы.Олардың арасы 100 бөлікке бөлініп, әрбір бөлік градус деп есептелінеді.Осындай екі шекті нүктесі бар термометр бүкіл Әлемде қолданысқа ие болды.

Жалпы бұндай температура шкаласының басты кемшілігі бар еді: мұздың қатуы мен судың қайнауы үшін қандай жағдай жасалуы керек деген сұрақ туындады.

Бір ғана тірек нүктесі бар термометрді қолданған ыңғайлы болар еді.Мысалы, мұздың балқу нүктесі.

Ең алғаш рет бір ғана тірек нүктесі бар шкала туралы идеяны 1873 жылы Д.И.Менделеев ұсынған екен.

Карно теоремасына негізделген Кельвин-Менделеев шкаласын бір ғана тірек нүктесі бар шкалалармен сәйкестендіру қиын емес.

Температураның термодинамикалық шкаласы(Кельвин-Менделеев шкаласы) - термометрлік заттық қасиетіне тәуелді болмайтын температураның абсолютті шкаласы( абсолютті нөл температурадан бастап саналады).Температураның термодинамикалық шкаласы термодинамиканың екінші бастамасына негізделіп жасалған.

Термодинамикалық температураның өлшем бірлігі- Кельвин(К). Судың үштік нүктесінің термодинамикалық температурасының ¹/_273,16  бөлігімен анықталады.

Сонымен қатар, термодинамикалық температура дегеніміз- термодинамикалық тепе-теңдік күйіндегі макроскопиялық жүйені сипаттайтын күй параметрі.Кейде оны абсолютті температура деп те атайды.

Табиғаттағы ең төменгі шектік температура- 273,15 °С-қа тең.Ол абсолютті нөл температура деп аталады.Өте төмен температуралар жөнінде айту артық болады.Себебі, термодинамиканың үшінші бастамасына сәйкес абсолюттік нөл немесе одан төмен температураны алу мүмкіндігі жоқ, себебі диаметрі нөлден кіші сым жасау мүмкін емес.

Халықаралық бірліктер жүйесінде температуралардың абсолюттік термодинамикалық шкаласы-Кельвин шкаласы қабылданған.Ол ХІХ ғасырдағы ағылшынның көрнекті ғалымы лорд Кельвиннің есімімен аталған.

Термодинамикалық шкаланың тұрақты нүктесі болып абсолютті нөл саналады.Бұл кезде молекулалардың жылулық қозғалысы тоқтап, олардың тек нөлдік деңгейдегі тербелісі қалады. Бұл кезде судың үштік нүктесі,яғни мұз, су және су буы термодинамикалық тепе-теңдікте болады. Термодинамикалық шкаланың екінші тірек нүктесіне су бір мезгілде қатты, сұйық және газ тәрізді-үш күйде қатар болатын температура қабылданған.Бұл күйді- үштік нүкте деп атайды.

Осы нүктелердің арақашықтығын тура 273,16 бөлікке бөлініп, оларға Кельвин деген атау берілген.Тура осындай бөлікке бөлінуінің басты себебі, температураның халықаралық шкаласы-Цельсий шкаласына (°С) сәйкестендіріліп алынған.Судың үштік нүктесінің темпеартурасы 0,01 °C болады, Яғни, 1 К-Цельсий шкаласы бойынша температура бірлігіне, яғни 1 градусқа тең: 1 K=1°С.

Цельсий шкаласы бойынша температура мен абсолютті термодинамикалық Кельвин шкаласы арасындағы байланыс:

T = (t°C+273,15)K немесе t°= (Т-273,15) °С (33)

Абсолютті шкаладағы судың қайнау температурасы 373 К болады.

Аталмыш температуралық шкаланы пайдаланып, температуранаы өлшеу термометрлік дене( спирт,сынап, газ) көлемінің өзгерісіне байланысты жүргізіледі,ол- температуралық шкаланы жасаудың бірден-бір мүмкін тәсілі.

Енді, энтропияның температурамен байланысын мына формула арқылы көрсетуге болады(34):

(34)

Планк постулатына сәйкес энтропия басқа да термодинамикалық функцияларға қарағанда басты ерекшелігі- санау нүктесінің болуы.Бұл-термодинамиканың үшінші бастамасында көрсетілген негізгі қағидалардың бірі.Яғни, абсолют нөл температурада барлық идеал кристалдардың энтропиясы бірдей болады және ол нөлге тең.

Температураға абсолют нөлге ұмтылған кезде, тек энтропия ғана нөлге ұмтылмайды.Сонымен қатар, оның барлық термодинамикалық параметрлерге қатысты туындылары да нөлге тең болады.

( x=p,V). (35)

Бұл дегеніміз – абсолют нөлге жақындаған барлық термодинамикалық үрдістер энтропияның өзгерісінсіз жүзеге асады деген сөз.Оны жылулық Нернст теоремасы деп атайды.

Абсолюттік нөл температураға жету мүмкін емес, сондықтан Нернст теоремасының дұрыстығы туралы тек заттың абсолюттік нөл температурасына жақын температурадағы заттың сипаттамаларының өзгерісіне қарап айтуға болады. Нернст теоремасын Больцман формуласымен, демек энтропияның ықтималдылық бойынша интерпретациясына сүйеніп түсіндіруге болады. Ол үшін жүйенің абсолюттік нөл температурадағы күйінің статистикалық салмағын табу керек. Бұл жерде классикалық әдіс жарамсыз болады. Себебі классикалық механика абсолюттік нөл температурада да жүйенің үздіксіз көптеген динамикалық күйлері болатындығын көрсетеді. Кванттық күй деп жүйенің жалпы күйін қарастырамыз, ал жүйенің өзі тұйықталған болуы керек. Абсолюттік нөл температурада жүйенің күйі минимал. Жүйенің мүмкін болатын кванттық күйлерінің саны минимал энергия деңгейі туындалған болмаса бірге тең, ал бұл деңгей туындалған болса бүтін сан болатын туындалу еселігіне тең болады. Осы санмен жүйенің статистикалық салмағы да өрнектеледі. Сондықтан Больцман формуласы бойынша энтропия мәні шекті мәнге тең болады.

Осы теореманың арқысында Планк постулаты абсолютті энтропия ұғымын енгізуге мүмкіндік береді.Қалыпты жағдайдағы заттың абсолютті энтропиясын есептеу үшін әрбір фазадағы заттың жылусыйымдылығының температураға және энтальпияның фазалық ауысуына тәуелділігін білу қажет.Мысалы, Т температурадағы газ тектес заттың абсолютті энтропиясы мынадай түрде жазылады:

(36)

Көбінесе, термодинамикалық кестелерде 298 К температурадағы қалыпты жағдайдағы абсолютті энтропияның мәндері беріледі.Бұл мәндер химиялық реакциялардың энтропия өзгерісін есептеу үшін қолданылады.