Практическое занятие 2

Тема: АЛГОРИТМЫ ПОИСКА МНОЖЕСТВА ПУТЕЙ

Контрольные вопросы

1. Алгоритмы поиска множества путей.

2. Основные правила и законы булевой алгебры.

3. Правила разложения булевых определителей.

4. Разложение булевого определителя структурной матрицы В.

5. Основные правила преобразования матрицы и определителей.

6. Возведение структурной матрицы В в степень.

7. Сетевой алгоритм поиска множества путей.

Основное назначение сети связи заключается в том, чтобы предоставлять абонентам соединительные пути для передачи сообщений в соответствии с адресами и требуемыми качественными показателями (качеством обслуживания, скоростью передачи, надежностью и т.д.); при этом выбор соединительных путей должен осуществляться таким образом, чтобы обеспечить наиболее эффективное использование оборудования сети, минимально возможную длину путей, число транзитных участков в путях, необходимое число каналов в путях и т.д.

При решении разных задач анализа и синтеза сетей связи возникает необходимость поиска множества путей, существующих между заданной парой узлов сети (вершин графа). Все методы поиска множества путей в сети можно поделить на два класса – матричные и сетевые.

Матричные методы основаны на преобразовании различных матриц – топологических или матриц характеристик ребер графа, сетевые – на присвоении вершинам графа некоторых обозначений, которые называют пометками (или индексами).

Алгоритмы поиска множества путей. Все алгоритмы поиска множества путей делятся на матричные и сетевые.

Матричные алгоритмы поиска множества путей делятся на:

– разложение булевого определителя структурной матрицы В;

– возведение структурной матрицы В в степень.

Разложение булевого определителя структурной матрицы В. Если в сети есть возможность передачи информации из узла i в узел j ( по прямым каналам или через промежуточные узлы), то говорят, что существует связь от i до j. Для осуществления связи должен существовать соответствующий путь или пути.

Введем следующие обозначения:

µ_ij – путь из узла i в узел j (из вершины i к вершине j графа);

m_ij – множество путей из узла i в узел j .

Путь µ_ij – это упорядоченный набор ребер, его составляющих.

Длина пути µ_ij – L_ij – это сумма длин l_xy ребер, его составляющих:

L_ij =

Ранг пути R _ij -число ребер, образующих путь.

Для графа, изображенного на рис. 2.1, для пути µ₁₄ = а₁₂, а₂₅, а₅₃, а₃₄ ранг R₁₄ = 4; для пути µ₁₄ = а₁₄ ранг R₁₄= 1; для пути µ_{14 =} а₁₂, а₂₃, а₃₄ ранг R₁₄ =3.

Структурная матрица графа черт. 2.1, представленная в табл. 2.1, может рассматриваться как булева матрица, поскольку ее элементами являются булевы переменные. Действительно, любой элемент матрицы В – это переменная, ее инверсия, константы 0 или 1. Таким образом, путь как последовательность ребер может быть представлен конъюнкциєю (логическим умножением) ребер, его составляющих. Рассмотренные пути µ₁₄ запишем в форме

µ₁₄ = agfc; µ₁₄ =h; µ₁₄ =abc

Множество путей можно записать в дизъюнктивной нормальной форме, применив операцию дизъюнкции (логического сложения) к путям, которые представляют множество.

Так, в рассматриваемом примере

m₁₄ = agfc + h + abc .

Здесь для обозначения логического умножения и сложения применяются символы алгебраического умножения и сложения. Кроме указанных символов, используются также символы: ٨ – для обозначения конъюнкції, ٧ – для обозначения дизъюнкции.

Таблица 2.1 – Структурная матрица графа, изображенного на рис. 2.1

В =

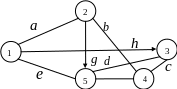
Рисунок 2.1 – Изображение графа структурной матрицы табл. 2.1

Множество путей m_ij может быть получено разложением определителя матрицы В, из которой предварительно вычеркивается столбец с номером i и строка с номером j , т.е.:

(2.1)

Разложение определителя матрицы В _іj проведено по строке с номером k. Разложение (2.1) можно проводить по любой строке (столбцу). Здесь В _іj – матрица, полученная из исходной структурной матрицы после вычеркивания i –го столбца и j –й строки.

В столбцах каждой вершины графа записаны ребра, в неё входящие; в строках каждой вершины графа записаны ребра, исходящие из вершины.

Вычеркнув столбец i и строку j, мы тем самым исключим те ребра, которые не могут образовывать путей множества m_ij. |В_kl | – определитель, полученный из det В_іj после вычёркивания k –й строки и l–го столбца.

Разложение определителя(2.1) нужно проводить по известным правилам линейной алгебры, однако операции алгебраического умножения и сложения заменяются на операции логического умножения и сложения, соответственно.

При преобразовании матрицы и определителей нужно использовать основные правила и законы булевой алгебры:

1). 1 + а = 1; 1·а = а;

2). 0 + а= а; 0·а = 0;

3). ; ;

4). а + а = а; а· а = а – закон повторения;

5). а + ab = а – закон поглощения;

6). (а + х) (а + у) = а + ху – распределительный закон.

При разложении булевых определителей необходимо также пользоваться следующими правилами:

1). определитель, который имеет единицу в каждой строке и столбце, тождественно равен единице;

2). если какая-либо строка или столбец состоит из нулей, то определитель тождественно равен нулю;

3). если перед определителем записан множитель «а», то все элементы «а» в определителе можно заменить на «1», а все элементы «а» в определителе можно заменить на «0»;

4). если в определителе поменять местами две строки или два столбца, или произвести его транспонирование, то значение определителя не изменится.

Рассмотрим получение множества путей m₁₄ из матрицы В (см.табл.2.1):

m₁₄ = det В _іj =

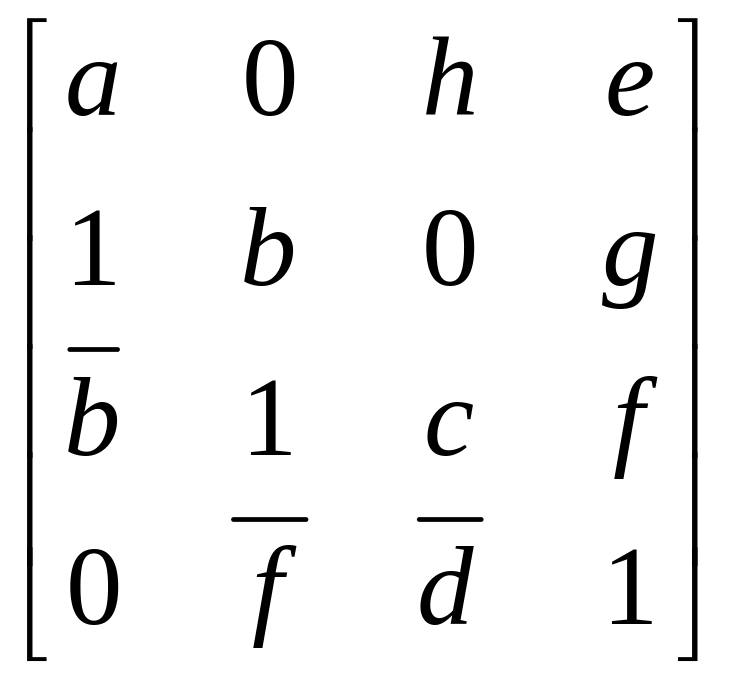
Разложение определителя проведем по столбцу с номером 4:

m₁₄=

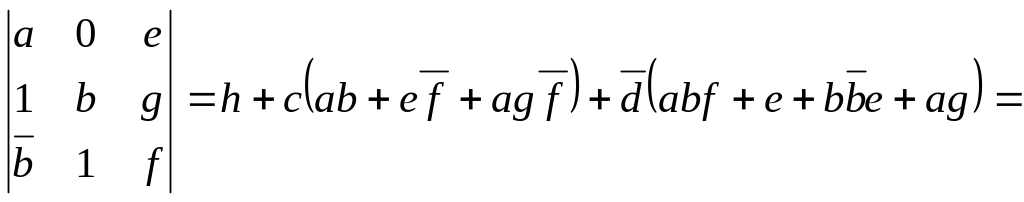
Упорядочим полученные пути по рангу, учтя последовательность ребер в путях. Получим:

m₁₄ =

Такой же результат получим, разложив определитель, например, по первой строке:

m₁₄ =

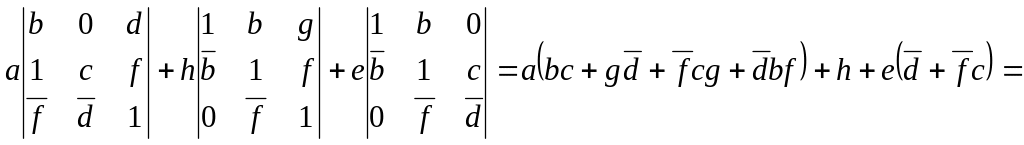
Возведение структурной матрицы В в степень. Начальная структурная матрица В является матрицей прямых связей, то есть в ней записаны все пути первого ранга, существующие в графе. При возведении матрицы в квадрат каждый ее элемент будет представлять множество путей до второго ранга включительно, существующих между вершинами i и j. Возведение матрицы В в степень Rmax= n – 1 приводит к получению всех путей, существующих между каждой парой (и,j) вершин графа, то есть:

Здесь n – число вершин графа, Rmax – максимально возможный ранг путей в графе. Rmax = n – 1 в случае, если какой-нибудь путь проходит через все вершины графа.

При возведении матрицы в степень пользуются известными правилами линейной алгебры:

В⁽²⁾ = В⁽¹⁾ · В⁽¹⁾ ,

В⁽³⁾ = В⁽²⁾ · В⁽¹⁾ и т.д.

Элемент матрицы – сомножителей С=A*D в линейной алгебре получают согласно выражения

(2.2)

n– общий размер матриц А і D (число столбцов матрицы А и строк матрицы D, в случае возведения квадратной матрицы B в степень n – число вершин).

Поскольку матрица В – булева, возведение ее в степень осуществляется с использованием законов и тождественностей булевой алгебры. Кроме того, в выражении (2.2) операции алгебраического умножения и сложения заменяют на операции логического умножения и сложения соответственно. При возведении матрицы В в степень q каждый элемент bij ^(q) матрицы В^(q) вычисляется по следующим правилам:

1) элементы і–ой строки матрицы В^(q-1) логически умножаются на соответствующие элементы j–го столбца матрицы В⁽¹⁾;

2) полученные логические сомножители логически складываются, образовывая искомое значение элемента bij ^(q). Если при возведении в некоторую степень q окажется, что В^(q) = В^(q-1) вычисление нужно прекратить. При этом В^(q) = В^(q-1) = =В^(Rmax) .

Покажем процесс получения матрицы B⁽²⁾ для графа рис. 2.1, матрица которого представлена в табл. 2.1.

Для получения элемента необходимо использовать элементы первой строки и второго столбца матрицы В⁽¹⁾ :

= − I строка В⁽¹⁾ ─ II строка В⁽¹⁾

Аналогично получим элементы матрицы B⁽²⁾:

и т.д.

Полученные результаты сведем в матрицу B⁽²⁾ (табл 2.2)

Таблица 2.2 – Матрица B⁽²⁾

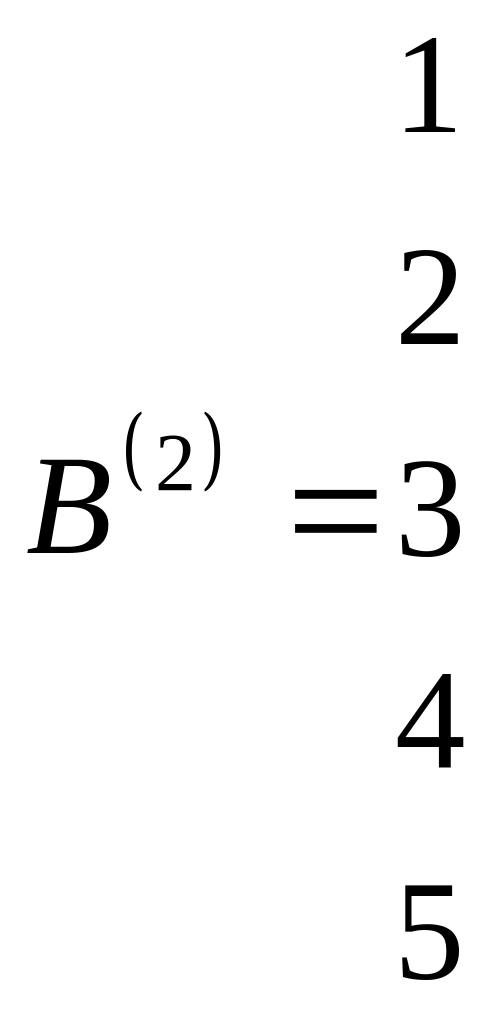
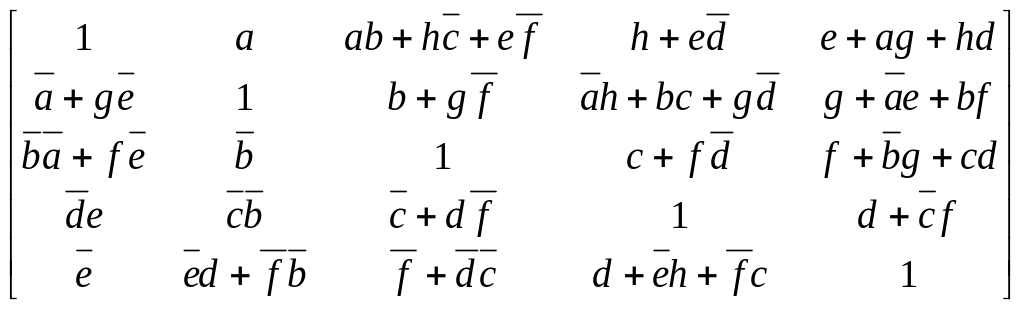
Из сравнения B⁽²⁾ и B⁽¹⁾ (табл.2.2 и 2.1) вытекает, что полученная матрица B⁽²⁾ не является результирующей, поскольку B⁽²⁾ ≠ B⁽¹⁾ и процесс вычислений нужно продолжать, а именно:

1. Вычислить B⁽³⁾ = B⁽²⁾B⁽¹⁾.

2. Если B⁽³⁾= B⁽²⁾ ,то B⁽³⁾= В^(Rmax) , результат получен.

Если B⁽³⁾ ≠B⁽²⁾ , продолжить вычисление, то есть получить B⁽⁴⁾

Поскольку R_max=4 для данного графа сети, матрица будет результирующей в любом случае, даже если B⁽⁴⁾ ≠ B⁽³⁾.

В полученной результирующей матрице В^(Rmax), как отмечалось раньше, каждый элемент bij^(Rmax)=mij , то есть определяет множество всех путей из вершины i в вершину j.

Итак,

и т.д.

Сетевой алгоритм поиска множества путей.

Сетевые методы определения множества путей между заданными узлами сети является графическим эквивалентом матричных методов.

Определение множества путей основано на построении дерева путей из фиксированной вершины-истока («корень» дерева) во все остальные вершины–стоки графа. Сетевые методы определения множества путей между заданными узлами сети является графическим эквивалентом матричных методов.

Для построения дерева путей необходимо прежде всего отметить «ярусы» дерева. На ярусе R=0 располагается вершина–исток – «корень» дерева. На ярусе R=1 располагаются вершины, смежные вершине–истоку, т. е. вершины, пути в которые из вершины-истока имеют ранг, равный единице. На ярусе R=2 располагаются вершины, смежные вершинам, расположенным на ярусе R=1, и т.д.

При записи вершин на ярус R=2 и последующие ярусы необходимо следить за тем, чтобы образующие пути рангов 2, 3 и т.д. были простыми (самонепересекающимися), т. е. чтобы ни одна вершина в пути не повторялась более одного раза.

Максимальное значение яруса (ранга пути) R_maх = n–1 (n –число вершин графа).

Дерево путей содержит все пути из фиксированной вершины–истока во все остальные вершины. При этом на ярусе 1 содержатся все пути первого ранга, на ярусе 2 – все пути второго ранга и т.д.

Таким образом, на некотором k-м ярусе содержится информация обо всех путях k-гo ранга из фиксированной вершины-истока графа во все остальные вершины.

Для графа черт. 2.1 построим дерево путей из вершины 1. Данная вершина является корнем дерева и помещается на нулевой ярус. Значение ранга пути здесь R=0. На первый ярус R=1 помещаются вершины 2, 4, 5, имеющие непосредственную связь с вершиной 1. Дальше на второй ярус от вершины 2 помещаются вершины, связанные с вершиной 2, а именно 3 и 5. Вершина 1 исключается из рассмотрения, поскольку путь в вершину 2 прошел через вершину 1.

От вершины 4 на второй ярус записываются вершины 3 и 5, от вершины 5- вершины 4 и 3. Аналогично записываются вершины на остальные ярусы дерева.

Построенное дерево для вершины-истока 1 представленное на рис. 2.2. Как видно, в дереве имеется три пути первого ранга (R=1): а, h, e; шесть путей второго ранга (R = 2): ab, ag, hс, hd, e , e , на третьем ярусе (R = 3) записаны пути третьего ранга: ab , abc, ag , ag , hc , hсf, hd , e , e c, e . Наконец, пути четвертого ранга (R = 4): ab , abсd, ag с, ag , hс g, hd b, e .

Естественно, из дерева можно получить множество путей из фиксированной вершины в любую вершину графа последовательным просмотром ярусов дерева. Так,

^.

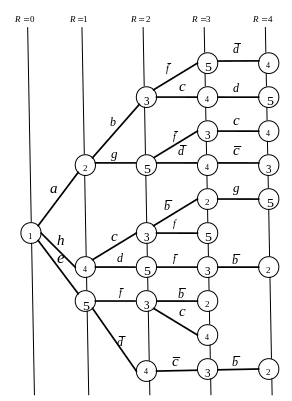
Рис. 2.2 – Дерево путей для вершины-истока 1.