Министерство науки и образования РФ

Федеральное государственное образовательное учреждение высшего профессионального образования

Волгоградский государственный технический университет

Кафедра

«Технология материалов»

Семестровая работа по дисциплине: «Механические свойства металлов»

Тема: «Вязкость разрушения. Взаимосвязь коэффициента интенсивности напряжений со структурой сплавов».

Выполнил: Власюк А.А

Группа: М – 435;

Проверил: доц.к.т.н

Водопьянов В.И.

Волгоград,2016.

Содержание:

Введение: 2

1.Теоретическая часть. 4

2.Экспериментальная часть. 7

3.Выводы: 9

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 10

Введение:

Способность тел сопротивляться распространению трещин обусловлена структурным состоянием материала и его механическими свойствами. В ходе развития трещины процесс разрушения контролируется свойствами материала у вершины дефекта.

В качестве характеристики, отражающей предельное состояние материала в локальном объеме у вершины трешины обычно используется вязкость разрушения где У - поправочный множитель, учитывающий геометрию плоского тела с трещиной. Кроме геометрических характеристик тел с дефектом. вязкость разрушения зависит от многих параметров, в первую очередь, от температуры и скорости нагружения , а также от проч-ностных характеристик материала, в частности, предела текучести , и размера зерна.

1.Теоретическая часть.

В ГОСТ 25.506-85 [3], посвященном характеристикам трещиностойкости при статическом нагружении, рекомендуется определение силовых, деформационных и энергетических критериев разрушения. В качестве основных рекомендуются испытания по определению критических значений коэффициентов интенсивности напряжений в условиях плоской деформации Кlc и Кс. Если известна величина Кlc для данного материала, то можно рассчитать величину напряжения, которое будет вызывать нестабильное разрушение при наличии в теле дефекта определённого размера и формы при наиболее жёстком напряжённом состоянии . То есть по коэффициенту Кlc и длине трещины можно найти напряжения, возникающие у вершины трещины, и оценить прочность конструкций. [2]

Для получения предварительных оценок роста и ветвления трещиноподобных дефектов в реальных материалах в условиях обобщенного напряженного состояния проведены эксперименты по трехточечному несимметричному изгибу балок, изготовленных из материалов, существенно различающихся по структурным, прочностным и деформационным характеристикам: алюминиевого сплава Д16Т, стали Cт. 3(Ст3сп ).В балках выполнялся пропил, имитирующий трещину, шириной 1,5 мм и глубиной l (в миллиметрах). Схема нагружения образцов, когда сосредоточенная сила P приложена в центре, а сжимающие напряжения σ < 0 — по торцам образцов, приведена на рис. 1. При этом длина образцов между опорами L = 100 мм, длина краевой трещины-пропила для балок из алюминиевого сплава Д16Т l = 7,5 мм, для стальных образцов l = 6,8 мм, расстояние от точки приложения сосредоточенной силы до трещины s = 30 мм, высота образцов из алюминиевого сплава Д16Т b = 20 мм, высота образцов из стали b = 17 мм, толщина всех образцов t ≈ 10 мм, α — угол излома траектории трещины. В табл. 1 приведены жесткостные, прочностные и деформационные характеристики алюминиевого сплава Д16Т и стали Cт. 3, полученные авторами данной работы в предварительных экспериментах, согласующиеся со справочными данными.

Рисунок 1- Схема нагружения образцов:сплошная линия — касательная, штриховая — траектория трещины.

Таблица 1- Характеристики материалов, из которых выполнены образцы.

Материал	E, МПа	σ02, МПа	σ ∗ , МПа	ν	ε ∗ , %
Сплав Д16Т	7 ·	400 ÷ 450	610	0,34	10 ÷ 12
Сталь Ст. 3	20·	220	400 ÷ 450	0,28	≈ 25

П р и м е ч а н и е. Для характеристик материала приняты следующие обозначения: E — модуль Юнга, σ02 — предел упругости, σ ∗ — предель- ные напряжения при разрыве, ν — коэффициент Пуассона, ε ∗ — предельное относительное удлинение, при котором происходит разрыв. [1]

Таблица 2-Химический состав

Марка стали	Содержание элементов , %
	C	Si	Mn	Ni	S	P	Cr	Cu	As	N	Fe
Cт. 3	0,14 - 0,22	0,15 - 0,3	0,4 - 0,65	до 0.3	до 0.05	до 0,04	до 0.3	до 0.3	до 0.08	до 0,008	~97

Марка стали	Fe	Si	Mn	Cr	Ti	Al	Cu	Mg	Zn	Примеси
Д16Т	до 0.5	до 0.5	0.3 - 0.9	до 0.1	до 0.15	90.9 - 94.7	3.8 - 4.9	1.2 - 1.8	до 0.25	прочие, каждая 0.05; всего 0.15

Для расчета величины вязкости разрушения по максимальной нагрузке предлагается следующая формула:

= ,

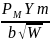где: 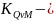условная вязкость разрушения коротких образцов;

– максимальная нагрузка испытания;

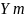– коэффициент минимальной интенсивности напряжений, для образцов с W/b = 1,45 ,Y m = 29,21;

b – диаметр образца;

W – длина образца. [2],

Откуда: =