Прямые методы синтеза
Название «прямые методы» означает, что в данном случае не используется аналоговый прототип. Исходными данными для синтеза служат какие-либо параметры фильтра (чаще всего – его АЧХ), которые могут задаваться, вообще говоря, произвольно.
Они делятся на две категории. На рисунке ниже представлен вид разделения.
оптимальные методы, в которых численными итерационными методами ищется минимум заданной функции качества;
субоптимальные методы, не дающие в точности оптимального решения, но позволяющие значительно упростить вычисления по сравнению с оптимальными методами. Как правило, эти методы используют специфику решаемой задачи, например дробно-рациональный вид функции передачи рекурсивного фильтра или экспоненциальный вид отдельных слагаемых его импульсной характеристики.
Оптимальные методы синтеза
Чаще всего отправной точкой при расчете фильтра служит его желаемая частотная характеристика – либо АЧХ (когда фазовые характеристики не важны), либо комплексный коэффициент передачи. В качестве минимизируемой меры отклонения характеристики фильтра от заданной в общем случае используется p-норма ошибки. Чаще всего используются два значения p: p = 2 (квадратическая ошибка) и р= ∞ (максимальное абсолютное значение ошибки).
Где е(х) = f(x) – g(x) – это величина ошибки в точке х, то есть разность между желаемой f(x) и фактической g(x) величинами.
Поскольку корень p-й степени при любом p является монотонно возрастающей функцией, при расчете минимизируемой величины его можно не вычислять.
Оптимальные методы синтеза
Если при синтезе фильтра нас интересует только его АЧХ, минимизируемая функция при использовании p-нормы ошибки рассчитывается следующим образом:
Где
D(
)
– желаемая АЧХ, |K(
)|
- АЧХ фильтра, w(
)
неотрицательная
вещественная весовая функция.
Использование весовой функции позволяет придать разную значимость различным участкам частотной оси. В частности, это дает возможность задать переходные зоны, поведение АЧХ в которых не имеет значения. В этих зонах значение весовой функции должно быть нулевым.
Если необходимо аппроксимировать заданную частотную зависимость комплексного коэффициента передачи, норма ошибки аппроксимации рассчитывается так:
Где р - степень(2, ∞); w – весовая функция.
В большинстве случаев задача минимизации функции (1) или (2) не имеет аналитического решения и должна решаться итерационными численными методами. Исключение составляет синтез нерекурсивного фильтра при р = 2, когда рассматриваемая оптимизационная задача приводит к системе линейных уравнений относительно коэффициентов фильтра.
При р = ∞ рассматриваемая норма ошибки равна максимальному абсолютному отклонению характеристики от заданной. Минимизация этой нормы соответствует минимаксной аппроксимации и дает фильтры с равномерными пульсациями АЧХ.
Метод Ремеза
Предназначен он для синтеза нерекурсивных фильтров путем минимаксной аппроксимации заданной АЧХ.
Синтаксис вызова функции следующий:
[b, delta, opt] = remez(n, f, a, w, ‘ftype’, {lgrid})
Где n – порядок фильтра;
f и a – векторы, совместно задающие АЧХ;
w – весовые коэффициенты для частотных полос;
ftype – ‘’, ‘hilbert’, ‘differentiator’.
Функция remez предназначена для синтеза нерекурсивных фильтров с линейной ФЧХ и кусочно-линейной АЧХ с возможными зонами неопределенности. Здесь n-порядок рассчитываемого фильтра (его импульсная характеристика будет содержать n+1 ненулевых отсчетов). Параметры f и a должны быть векторами одинаковой четной длины, они совместно определяют желаемую АЧХ синтезируемого фильтра. Вектор f содержит значения частот, нормированные к частоте Найквиста, а вектор a – соответствующие этим частотам значения АЧХ. В промежутках между заданными точками АЧХ интерполируется по линейному закону. Частоты в векторе f должны образовывать строго возрастающую последовательность.
Синтезируемая АЧХ определяется следующим образом:
- в полосах частот от f(2k-1) до f(2k) АЧХ линейно меняется от a(2k-1) до a(2k). Здесь k целые числа от единицы до половины длины векторов f и a;
- в полосах частот от f(2k) до f(2k+1) АЧХ считается незаданной и в процессе синтеза может оказаться произвольной.
Остальные параметры являются необязательными. Параметр w задает весовые коэффициенты для оптимизируемых частотных полос. При отсутствии параметра ftype производится синтез фильтра с симметричной импульсной характеристикой, при его наличии – с несимметричной.
Параметр {lgrid} задает плотность сетки частот. Выходной параметр delta содержит величину пульсаций АЧХ полученного фильтра. Выходной параметр opt представляет собой структуру, содержащую дополнительную информацию.
В качестве примера синтезируем ФНЧ 32-го порядка, имеющий полосу пропускания в диапазоне от 0 до 0.2 от частоты Найквиста, переходной зоной от 0.2 до 0.25 и полосой задерживания от 0.25 до 1.
Код программы и результат выполнения, представлен на рисунках ниже.
» n = 32; %порядок фильтра » f = [0 0.2 0.25 1]; %вектор частот » a = [1 1 0 0]; %значение желаемой АЧХ » [b, delta, opt] = remez(n, f, a); Расчёт фильтра » plot(reshape(f,2,length(f)/2), reshape(a,2,length(a)/2), 'g'); %график желаемой АЧХ » hold on » [h,w] = freqz(b); %комплексный коэффициент передачи » plot(w./pi, abs(h)); %график полученной АЧХ
Рисунок - Результат выполнения программы
Как уже говорилось, субоптимальные методы синтеза дискретных фильтров позволяют упростить вычисления за счет учета специфики решаемой задачи. При этом, в частности, может использоваться тот факт, что коэффициенты числителя функции передачи фильтра линейно связаны с его частотной характеристикой и потому влияют на ее форму значительно слабее, чем коэффициенты знаменателя. Кроме того, для поиска коэффициентов знаменателя часто используются методы авторегрессионного анализа.
Субоптимальный синтез с использованием окон предназначен для синтеза нерекурсивных фильтров.
Идея
его очень проста. Прежде всего мы задаем
желаемый комплексный коэффициент
передачи
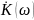в
виде непрерывной функции, определенной
в диапазоне частот от нуля до частоты
Найквиста, (если синтезируется вещественный
фильтр) или до частоты дискретизации
(если проектируется комплексный фильтр).
Обратное преобразование Фурье этой
характеристики, вычисленное с учетом
ее периодического характера
,
даст бесконечную в обе стороны
последовательность отсчетов импульсной
характеристики h(k).
Для получения реализуемого нерекурсивного фильтра заданного порядка эта последовательность h(k) усекается – из нее выбирается центральный фрагмент нужной длины. Из-за усечения первоначально заданная частотная характеристика искажается. Появляются переходные полосы между областями пропускания и задерживания, наблюдаются колебания коэффициента передачи в полосах пропускания, а в полосах задерживания АЧХ, как правило, приобретает лепестковый характер. Для ослабления эффектов искажений, h(k) умножается на весовую функцию (окно), плавно спадающую к краям.
В качестве примера рассчитаем нерекурсивный фильр(ФНЧ) 32-го порядка с частотой среза, равной ¼ от частоты Найквиста. Прежде всего рассчитаем бесконечную импульсную характеристику. Обратное преобразование Фурье от интересующей нас АЧХ (ФЧХ считаем нулевой) дает следующее (1).
Для получения фильтра 32-го порядка выбираем 33 отсчета этой импульсной характеристики, расположенных симметрично относительно нуля, то есть используем k= -16 … 16.
Выбор симметричного фрагмента бесконечной импульсной характеристики позволяет получить фильтр с линейной ФЧХ и, следовательно, постоянной групповой задержкой, равной (в отсчетах) половине порядка фильтра.
Код программы:
» к = (-16:16)';
» b = sinc(k/4)/4; %импульсная характеристика
» impz(b); % график импульсной характеристики
» figure % новое графическое окно
» [h, f] = freqz(b, 1, [], 2); %ЧХ фильтра
» plot(f, 20*1og10(abs(h))); % график АЧХ в децибелах
» ylim([-50 50]); %ограничение по оси у
» grid on %включаем линии сетки
Построим графики импульсной характеристики полученного фильтра и его АЧХ. Из графика АЧХ видно, что уровень боковых лепестков составляет -21 дБ, а их ширина равна 1/32 от частоты дискретизации. Рисунок представлен ниже.
Теперь воспользуемся какой-либо весовой функцией, например, окном Хэмминга, которое используется по умолчанию при синтезе фильтров данным методом в MATLAB (функции fir1 и fir2). Как видно, уровень лепестков в полосе задерживания упал примерно до -52 дБ за счет некоторого расширения полосы пропускания.