Под проектированием (синтезом) цифрового фильтра понимается выбор таких наборов коэффициентов фильтра удовлетворяют заданным требованиям. Строго говоря, в задачу проектирования входит и выбор подходящей структуры фильтра с учетом конечной точности вычислений. Это особенно актуально при реализации фильтров «в железе» - с использованием специализированных БИС или цифровых сигнальных процессоров.
В первую очередь надо определиться, какой тип цифрового фильтра мы хотим использовать. Существует два распространенных типа фильтров с бесконечной и конечной импульсной характеристикой – БИХ и КИХ.
КИХ фильтры обычно используют из-за их огромного преимущества – линейности фазовой характеристики, что во многих приложениях может быть жизненно необходимым. В остальных случаях используют БИХ фильтры, поскольку они значительно более эффективны.
Особенностью БИХ фильтров является возможность самовозбуждения при недостаточной разрядности коэффициентов фильтра или неправильном расчете передаточной характеристики. Для того, чтобы уменьшить влияние ограниченной разрядности коэффициентов, БИХ фильтры синтезируют последовательным соединением секций БИХ фильтров малого порядка (обычно 2-го порядка).
Проектирование фильтра производится в среде Filter Design & Analysis Tool.
В пакете Signal Processing имеется две графические среды, позволяющих рассчитывать и анализировать дискретные фильтры. Это среда fdatool (Filter Design & Analysis Tool) и блок работы с фильтрами, входящий в более старую универсальную среду sptool. В программе fdatool поддерживаются больше методов синтеза.
Для запуска программы расчета фильтров необходимо набрать ее имя в
командной строке MATLAB: >> fdatool
После этого появится окно программы, показанное на рисунке.
Рисунок – среда fdatool
Методы синтеза цифровых фильтров можно классифицировать по различным признакам:
По типу получаемого фильтра:
А) методы синтеза рекурсивных фильтров.
Б) методы синтеза нерекурсивных фильров.
2) по наличию аналоговых прототипов:
А) методы с использованием аналоговых прототипов.
Б) методы без использования аналового прототипа(прямые методы).
Синтез рекурсивных фильтров по аналоговому прототипу.
При синтезе дискретного фильтра по аналоговому прототипу необходимо реализовать переход из H(s) →H(z) s-области в z-область, то есть преобразовать функцию передачи аналогового фильтра в функцию передачи дискретного фильтра. Получающийся дискретный фильтр не может быть полностью идентичен аналоговому по своим характеристикам – хотя бы потому, что частотные характеристики дискретного фильтра являются периодическими. Можноговорить об определенном соответствии характеристик аналогового и дискретного фильтров.
Далее рассмотрим два метода синтеза рекурсивных дискретных фильтров по аналоговым прототипам:
Метод билинейного z-преобразования
Метод инвариантной импульсной характеристики.
Метод билинейного z-преобразования
Билинейное z-преобразование:
2fД
Метод билинейного z-преобразования позволяет синтезировать рекурсивный дискретный фильтр по частотной характеристике аналогового прототипа.
Функция передачи аналогового фильтра представляет собой дробно-рациональную функцию переменной s. Чтобы получить функцию передачи дискретного фильтра, необходимо перейти из s-области в z-область, причем дробно-рациональный характер функции должен сохраниться. Поэтому замена для переменной s должна представлять собой также дробно-рациональную функцию переменной z. Чтобы частотные характеристики аналогового и дискретного фильтров были связаны простой зависимостью, искомая замена переменной должна отображать мнимую ось в s-области на единичную окружность в z-области. В этом случае частотные характеристики аналогового и дискретного фильтров будут связаны лишь трансформацией частотной оси и никаких искажений «по вертикали» не будет.
Простейшей из функций, удовлетворяющей перечисленным требованиям, является билинейное z-преобразование (bilinear transformation) (1).
Связь
частотных характеристик:
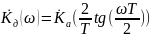
На
низких частотах
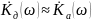
Частотные
характеристики аналогового
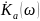и
дискретного
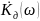фильтров
связаны
друг с другом лишь трансформацией
частотной оси (1).
На
низких частотах, когда
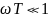тангенс
примерно равен своему аргументу, так
что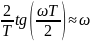
если
.
Поэтому в области низких частот частотные
характеристики
аналогового и дискретного фильтров
почти совпадают. Далее, по мере ускорения
роста функции тангенса, частотная
характеристика дискретного фильтра
все сильнее сжимается по горизонтали
(по сравнению с аналоговым прототипом)
и на частоте Найквиста, равной
π/Т,
достигает значения, которое частотная
характеристика аналогового фильтра
имела бы на бесконечной частоте.
Для
получения дискретного фильтра с заданными
частотами среза необходимо
скорректировать
частоты среза аналогового прототипа
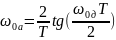, чтобы
компенсировать
искажения
частотной оси. Так, для синтеза дискретного
ФНЧ с частотой среза
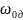аналоговый фильтр-прототип должен иметь
частоту среза
,
связанную с
следующим образом.
При билинейном z-преобразовании левая половина s-плоскости отображается внутрь единичной окружности на z-плоскости, поэтому синтез по устойчивому аналоговому прототипу даст гарантированно устойчивый дискретный фильтр.
Функция bilinear
Функция bilinear предназначена для синтеза дискретных фильтров по произвольным аналоговым прототипам методом билинейного z-преобразования. Она может преобразовывать заданные различными способами аналоговые описания систем в дискретные и поэтому имеет три варианта синтаксиса:
[bz, az] = bilinear (b, a, Fs, Fp);
[zz, pz, kz] = bilinear(z, p, k, Fs, Fp);
[Az, Bz, Cz, Dz] = bilinear(A, B, C, D, Fs, Fp)
Где Fs – частота дискретизации;
Fp – частота, на которой коефициенты передачи аналоговой и дискретной систем будут совпадать.
Аналоговый прототип при использовании функции bilinear должен быть физически реализуемым, то есть степень полинома числителя функции передачи не должна превышать степень полинома ее знаменателя. Параметр Fs задает частоту дискретизации в герцах. Последний входной параметр Fp является необязательным. Если он задан, то он задает частоту в герцах, на которой коэффициенты передачи аналоговой и дискретной систем будут совпадать.
В качестве примера рассмотрим синтез дискретного фильтра по аналоговому прототипу методом билинейного преобразования с частотой дискретизации 1 Hz. Код программы приведён ниже:
hold on;
>> b = [1 2 3 4];
>> a = [-0.4 0.9 -0.1 0.8]; %Коэффициенты знаменателя ф-ции передачи
>> [h, w] = freqs (b, a); % комплексный коэффициент передачи
>> p1 = plot (w, abs(h));
>> set(p1, 'Color','blue');
>> [bd, ad] = bilinear(b, a, 1); % Синтез дискретного фильтра
>> [hd, wd] = freqz(bd, ad); % Комплексный коэффициент передачи
>> p2 = plot(wd, abs(hd));
>> set(p2, 'Color','green');
>> legend('Аналоговый','Дискретный');
>> grid on;
>> axis([0 5 0 15]);
Представлен результат работы программы.
В пакете Signal Processing имеются готовые функции расчета фильтров Баттерворта, Чебышева 1-го и 2-го рода, а также эллиптических фильтров. Они выполняют расчет дискретных ФНЧ, ФВЧ, полосовых и режекторых фильтров по аналоговым прототипам Баттерворта, Чебышева (1-го и 2-го рода) и эллиптических фильтров методом билинейного z-преобразования.
Butter(n, w0, type) – расчёт фильтра Баттерворта
Cheby1(n, Rp, w0, type) – Чебышева 1-го рода
Cheby2(n, Rs, w0, type) – Чебышева 2-го рода
Ellip(n, Rp, Rs, w0, type) –эллиптических
Где n – порядок фильтра прототипа;
Rp – уровень пульсации АЧХ в полосе пропускания;
Rs – уровень пульсации АЧХ в полосе задерживания;
w0 – частота среза;
type – тип фильтра(‘’, ‘high’, ‘stop’)
Перечисленные функции могут рассчитывать как дискретные, так и аналоговые фильтры. Признаком дискретного расчета служит отсутствие строки ‘s’ в конце списка входных параметров.
Рассмотренные функции расчета фильтров требуют задания в качестве входных параметров порядка фильтра и его частоты среза. При этом понятие частоты среза для фильтров разных типов определяется по-разному. Однако исходными данными при разработке фильтров, как правило, являются другие параметры: частотные границы полос пропускания и задерживания, а также допустимая неравномерность АЧХ в полосе пропускания и минимально необходимое затухание в полосе задерживания.
Выбрать минимально необходимый порядок фильтра позволяют следующие однотипные функции пакета Signal Processing:
[n, Wn] = buttord (Wp, Ws, Rp, Rs);
[n, Wn] = cheb1ord (Wp, Ws, Rp, Rs);
[n, Wn] = cheb2ord (Wp, Ws, Rp, Rs);
[n, Wn] = ellipord (Wp, Ws, Rp, Rs);
Где:
Rp –Допустимый уровень пульсации в полосе пропускания(в децибелах);
Rs – минимально необходимое затухание в полосе задерживания (в децибелах);
Wp и Ws –граници полос пропускания и задерживания(нормированные к частоте Найквиста).
В качестве примера зададим очень жесткие требования к АЧХ фильтра нижнихчастот – узкую переходную полосу, малые пульсации в полосе пропускания и большое затухание в полосе задерживания - и посмотрим, каким окажется минимальный порядок фильтра Баттерворта.
Результат показывает, что для фильтра Баттерворта требуется очень большой порядок.
Код программы:
>> Wp = 0.2; % конец полосы пропускания
>> Ws = 0.21; % начало полосы задерживания
>> Rp = 1; % пульсации АЧХ в полосе пропускания(дБ)
>> Rs = 60; %затухание в полосе задерживания(дБ)
>> [n, Wn] = buttord(Wp, Ws, Rp, Rs)
n =145
Wn =0.2009