
- •Завдання № 10 кінематична схема механізму пресу
- •1. Вступ
- •Передумови розробки, її цілі і призначення:
- •2. Кінематичний аналіз механізму
- •2.1. Основні задачі кінематичного дослідження
- •2.2. Поняття масштабного коефіцієнта
- •2.3 Побудова планів положень механізму
- •2.4 Визначення швидкостей повзуна
- •3. Динамічний аналіз механізму
- •3.1 Приведення сил корисного опору до кривошипа і побудова графіка приведеного моменту
- •3.2 Визначення роботи сил корисного опору, роботи рушійних сил та моменту рушійних сил
- •2. Вибір двигуна
- •3. Підбір редуктора
- •4.Кінематичний розрахунок приводу
- •5. Розрахунок клинопасової передачі
- •6. Розрахунок відкритої зубчастої передачі
- •7. Розрахунок валу
- •8. Перевірочний розрахунок підшипників
- •9. Вибір шпонки
- •Список використаної літератури
2.2. Поняття масштабного коефіцієнта
Масштабний коефіцієнт μ – це ціла або дробова частина, яка визначає відношення дійсної фізичної величини, вираженій у відповідній розмірності, до відрізку, який на кресленні представляє цю фізичну величину в міліметрах.
Масштабний коефіцієнт фактичних розмірів при побудові планів положень механізму:
 м/мм
м/мм
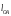 - дійсна
довжина ланки
- дійсна
довжина ланки
 ,
м;
,
м;
- довжина відрізки, який зображує ланку довжиною на кресленні, мм.
Масштабний коефіцієнт швидкостей при побудові плану швидкостей:
 (м/с)/мм
(м/с)/мм
де
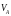 - фактичне значення лінійної швидкості
точки
- фактичне значення лінійної швидкості
точки
 ,
м/с;
,
м/с;
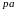 - довжина
відрізку що зображує вектор лінійної
швидкості
на плані швидкостей, мм.
- довжина
відрізку що зображує вектор лінійної
швидкості
на плані швидкостей, мм.
Масштабний коефіцієнт сили при побудові графіка сили корисного опору:
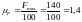 кН/мм.
кН/мм.
Масштабний коефіцієнт моменту сили при побудові графіку моменту сил корисного опору та моменту рушійних сил:
(кН∙м)/мм.
2.3 Побудова планів положень механізму
Плани
положень механізму – це кінематична
схема механізму, зафіксована в довільний
проміжок часу, або для якогось положення
кривошипу
 .
.
Основна задача побудови планів положень механізму – це визначення крайніх (нульових) точок, що визначають робочий хід.
В курсовій роботі необхідно побудувати 12 планів положень механізму, які відповідають 12 положенням вхідної ланки .
Для визначення робочого ходу повзуна розіб’ємо повний оборот в 360° ведучої ланки – кривошипа на 12 однакових частин по 30° кожна. Для кожного положення кривошипа побудуємо план положень ланок механізму. В результаті отримаємо 12 положень повзуна. З них 2 є крайніми.
Якщо
потрібно, для більш точного визначення
кожного з двох крайніх положень повзуна
ту частину в
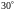 повного обороту кривошипа, якій
відповідають попередньо крайнє і
найближче до нього положення повзуна,
розіб’ємо
на 3 підчастини по
повного обороту кривошипа, якій
відповідають попередньо крайнє і
найближче до нього положення повзуна,
розіб’ємо
на 3 підчастини по
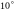 кожна і для них побудуємо плани положень
ланок механізму.
кожна і для них побудуємо плани положень
ланок механізму.
З
отриманих двох крайніх положень повзуна
те, від якого повзун рухається назустріч
силі коричного опору
 ,
приймемо за початок робочого ходу(нульове
положення). Після цього введемо нумерацію
положень рухомих кінематичних пар: для
прямого ходу повзуна назустріч силі
– з індексами від 0 до 6, для зворотнього
ходу – з індексами від 6 до 12 (12 співпадає
з 0).
,
приймемо за початок робочого ходу(нульове
положення). Після цього введемо нумерацію
положень рухомих кінематичних пар: для
прямого ходу повзуна назустріч силі
– з індексами від 0 до 6, для зворотнього
ходу – з індексами від 6 до 12 (12 співпадає
з 0).
Описані операції виконані на плакаті “Кінематично-динамічне дослідження механізму”.
2.4 Визначення швидкостей повзуна
Швидкості повзуна в кожний з 12 моментів часу , що розглядаються , знайдемо графоаналітичним методом планів швидкостей .
План швидкостей – це місце, де шуканий вектор швидкості отримують шляхом складання (за правилами складання векторів) відомих векторів швидкостей та векторів швидкостей з відомою лінією дії (направленням).
Спочатку
виберемо центр
 плану швидкостей , який відповідає
нерухомим точкам механізму
(
плану швидкостей , який відповідає
нерухомим точкам механізму
( ).
Далі
виберемо масштаб
).
Далі
виберемо масштаб
 для зображення векторів швидкостей на
плані швидкостей .
для зображення векторів швидкостей на
плані швидкостей .
Визначимо аналітично швидкість кривошипа за формулою:
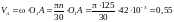 м/с.
м/с.
За
направленням
 .
Зобразимо
її на плані швидкостей вектором
.
Зобразимо
її на плані швидкостей вектором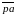 :
:
 ,
,
 .
.
Швидкість
наступної точки В , яка пов’язана через
ланки механізму з точками
 і
і
 ,
швидкості яких уже відомі, знайдемо
шляхом сумісного розв’язання системи
векторних рівнянь:
,
швидкості яких уже відомі, знайдемо
шляхом сумісного розв’язання системи
векторних рівнянь:
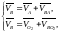
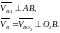
Де
 ,
,
 - відносні швидкості точки В у її
обертальному русі навколо точок А і
відповідно
(відомі тільки направлення (лінії дії)
цих швидкостей). Ці рівняння складаємо
на плані швидкостей, де їх запис має
вигляд:
- відносні швидкості точки В у її
обертальному русі навколо точок А і
відповідно
(відомі тільки направлення (лінії дії)
цих швидкостей). Ці рівняння складаємо
на плані швидкостей, де їх запис має
вигляд:
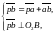
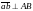 (1.1)
(1.1)
Порядок розв’язання системи (1.1):
Розв’язання
першого рівняння: в кінці (точка
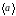 )
відомого вектора
(
)
відомого вектора
( )
проводимо лінію дії вектора
(
),
яка
перпендикулярна до ланки
)
проводимо лінію дії вектора
(
),
яка
перпендикулярна до ланки
 на кінематичній схемі.
на кінематичній схемі.
Розв’язання
другого рівняння:
через центр
проводимо лінію дії
вектора

( ),
яка перпендикулярна до ланки
),
яка перпендикулярна до ланки
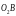 на кінематичній схемі.
на кінематичній схемі.
Розв’язок
системи (1.1) – точка
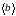 перетину побудованих двох ліній дій,
вектор
є зображенням швидкості
точки
В з кінематичної схеми.
перетину побудованих двох ліній дій,
вектор
є зображенням швидкості
точки
В з кінематичної схеми.
Далі є 2 різновиди схем.
В
схемах першого різновиду
між повзуном С і точкою В, швидкість
якої вже знайдена, знаходиться додаткова
обертальна кінематично пара (точка D)
, додаткова обертальна кінематична
пара (точка
D)
, прочому
точки B
і O2
розташовані
на одній
прямій.
В цьому випадку швидкість
точки D
знаходимо за допомогою теореми подібності
ланки (прямої фігури
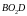 )
плану швидкостей цієї ланки (прямої
фігури
)
плану швидкостей цієї ланки (прямої
фігури
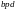 ):
):
 положення точки
d,
а значить і
швидкість
точки D
(
положення точки
d,
а значить і
швидкість
точки D
( ).
Швидкість
повзуна С знаходимо так само, як і
в схемах другого різновиду , де замість
швидкості
використовуємо
).
Швидкість
повзуна С знаходимо так само, як і
в схемах другого різновиду , де замість
швидкості
використовуємо
 .
.
В схемах другого різновиду з кінематичною парою (точкою В) безпосередньо пов’язаний через шатун повзун С. В цьому випадку швидкість повзуна С знаходимо шляхом сумісного розв’язання системи умов:
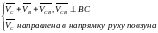
Ці умови на плані швидкостей мають вид
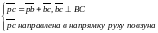 (1.2)
(1.2)
Порядок розв’язання системи (1.2):
Розв’язання
першого рівняння: в кінці (точка
)
відомого вектора
(
)
проводимо
лінію дії вектора
 ,
яка перпендикулярна до ланки ВС на
кінематичній схемі.
,
яка перпендикулярна до ланки ВС на
кінематичній схемі.
Виконання
другої умови: через центр
проводимо лінію дії вектора
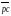 (
( ),
яка паралельна напрямку руху повзуна
С.
),
яка паралельна напрямку руху повзуна
С.
Розв’язок
системи (1.2) – точка
 перетину побудованих двох ліній дій,
вектор
є зображенням шуканої швидкості
повзуна
С:
перетину побудованих двох ліній дій,
вектор
є зображенням шуканої швидкості
повзуна
С:

Описані операції виконані на плакаті «Кінематично-динамічне дослідження механізму»
Швидкості повзуна для семи його положень, які він займає на прямому ході, приведень і табл 1.1
Табл.1.1
Положення повзуна |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Швидкість повзуна м/с |
0 |
… |
… |
… |
… |
… |
0 |
