48. Мп довгого соленоїда. Індуктивність довгого соленоїда

Циркуляцією вектора  по замкненому контуру називається інтеграл  де  - вектор елементу довжини контура, напрямлений вздовж обходу контура,  – проекція  на дотичну до контура, α – кут між  та  (рис. 4.9).

Розглянемо найпростіший випадок – магнітне поле нескінченно довгого прямолінійного струму. Лініями напруженості цього поля є кола, центри яких лежать на осі провідника, а площини перпендикулярні до нього.

Знайдемо циркуляцію  вздовж кола радіусом R:

, (4.15)

бо  .

В загальному випадку, коли провідник охоплений замкненою лінією довільної форми (рис. 4.10, а),

,

. (4.16)

Якщо контур не охоплює провідник зі струмом (рис. 4.10, б), то в (4.16)  адже радіальна пряма спочатку рухається в одному напрямку (ділянка 1-2,  ), а потім – в іншому (ділянка 2-1,  ). Отже,

. (4.17)

Якщо магнітне поле створюється кількома струмами  , то за принципом суперпозиції  і, враховуючи (4.16), остаточно одержимо

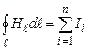. (4.18)

Ця формула є математичним виразом теореми про циркуляцію вектора напруженості магнітного поля: циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі сил струмів, охоплених даним контуром (позитивним вважається струм, що зв’язаний з напрямком обходу правилом свердлика; струм протилежного напрямку вважається негативним). Вираз (4.18) є математичною ознакою вихрового характеру магнітного поля.

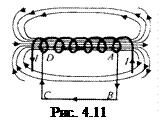
Використаємо теорему про циркуляцію  для розрахунку магнітного поля довгого соленоїда – циліндричної котушки, на яку намотано N витків дроту. Виберемо контур інтегрування у вигляді прямокутника ABCD, в якому сторона AD лежить всередині соленоїда і паралельна до його осі, а сторона ВС дуже віддалена від соленоїда (рис. 4.11).

Тоді згідно з (4.18)

. (4.19)

Магнітне поле соленоїда швидко зменшується при віддалені від нього, тому  . Крім того,  оскільки проекція на сторони AB і CD дорівнює нулю.

Отже, в лівій частині (4.19) залишається один доданок

.

Проекція  на паралельний йому відрізок DA дорівнює модулю цього вектора:  , а  (довжина сторони DA).

Таким чином,

 

 і  , (4.20)

де  – кількість витків на одиниці довжини соленоїда (густина витків). Отже, напруженість магнітного поля всередині довгого соленоїда дорівнює добутку сили струму на густину витків, а індукція поля

. (4.21)

 

49. Енергія мп. Густина енергії

Щоб зарядити провідник, треба виконати роботу проти кулонівських сил електростатичного відштовхування між однойменно зарядженими частинками. Так, для збільшення заряду на dq слід виконати роботу   , але   , тобто  . Отже, повна робота при електризації провідника від потенціалу 0 до потенціалу φ дорівнює:   .

За законом збереження енергії, робота з електризації йде на збільшення енергії зарядженого провідника, а отже   − є енергією електростатичного поля навколо провідника.

Енергія електричного поля для конденсатора може бути обрахована з останньої формули:   . Враховуючи, що   , а значить,  , маємо   . Але S·d=V − об’єм поля між пластинами конденсатора. Густина енергії − енергія, яка припадає на одиницю об’єму, тобто   .

Знаючи об’ємну густину енергії ω_Е , можна визначити загальну енергію довільного електростатичного поля. Так, якщо поле неоднорідне, то його можна розділити на нескінченно малі об’єми, в межах яких поле − однорідне. Тоді повна енергіяелектростатичного поля в довільному об’ємі V:

 . 50. Струм зміщення. Узагальнений закон повного струму

Розглянемо рівняння Дж. Максвела в інтегральному вигляді.

1.        Теорема Остроградського−Гаусса: потік вектора електричного зміщення через довільну замкнену поверхню, що обмежує електричні заряди дорівнює алгебраїчній сумі останніх:

 ,

де ρ − об’ємна густина заряду; dV − елемент об’єму всередині поверхні.

        Це фактично відома теорема  Гауса стосовно потоку ліній індукції електричного поля і стверджує, що лінії індукції    можуть починатись та закінчуватись лише на заряджених частинках чи тілах, тобто що електростатичне поле обов’язково пов’язане із зарядженими тілами.

2.        Узагальнений закон повного струму (закон Максвела−Ампера). Розглянемо довільний контур, який охоплює провідник зі струмом та розіб’ємо його на елементарні ділянки Δl ( рис.13.4). Як відомо, Ампер встановив, що сума добутків  довжин елементарних ділянок на складову вектора    пропорційна результуючій силі струму, тобто  , а оскільки    , то можна записати, що    .

       Максвелл узагальнив даний закон та подав його у вигляді:

 ,

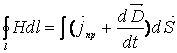тобто, циркуляція вектора напруженості магнітного поля по довільному контуру  дорівнює повному струмові, що пронизує будь-яку поверхню, пов’язану із даним контуром.

       Це рівняння стверджує, що навколо будь-якого струму провідності та змінного електричного поля неодмінно існує вихрове магнітне поле, причому     _┴   .

3.        Закон електромагнітної індукції Фарадея: змінне в часі магнітне поле породжує навколо себе вихрове електричне поле:

 .

       Це рівняння є узагальненням явища електромагнітної індукції та стверджує, що змінне в часі магнітне поле утворює вихрове електричне поле. Лінії напруженості електричного поля    охоплюють лінії індукції магнітного поля    у вигляді замкнутих кривих.

4.         Магнітний потік через довільну замкнуту поверхню завжди дорівнює нулю

 ,

тобто поле вектора    являється чисто вихровим.

                   Це рівняння виражає теорему Гауса відносно потоку ліній магнітної індукції через довільну замкнуту поверхню і стверджує, що ці лінії завжди замкнуті.

                   Рівняння Максвела виражають основні закони електромагнетизму. Головний висновок можна сформулювати так. Електричне та магнітне поле можна розглядати окремо, якщо вони незмінні в часі. Якщо ж вони змінні в часі, то розглядати їх окремо не можна, оскільки змінне в часі магнітне поле породжує змінне в просторі електричне, а змінне в часі електричне − призводить до виникнення змінного в просторі магнітного поля. Отже, головним висновком є умова виникнення електромагнітних хвиль. Цей висновок для вакууму в загальному можна математично описати системою рівнянь: