32. Циркуляція мп. Закон повного струму. Вихровий характер мп

Ц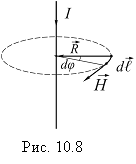 иркуляцією вектора напруженості   магнітного поля вздовж замкнутого контуру L називається інтеграл вигляду  , де H_l − складова вектора Н у напрямку контура, dl − елемент довжини контуру.

З електродинаміки відомо, що циркуляція сторонніх сил дорівнює ЕРС джерела, тому циркуляцію вектора напруженості магнітного поля вздовж  замкнутого контуру називають магніторушійною силою ε_m.

Розглянемо найпростіший випадок: визначимо ε_m вздовж якоїсь лінії напруженості магнітного поля прямого струму. З рис. 10.8    , тоді   , або можна записати   .

Це рівняння справджується для будь-яких провідників довільної конфігурації, не залежить від природи струму і форми замкнутого контуру.

Якщо контур охоплює струми І₁, І₂,...., І_n, то остання формула має вигляд  . Цим рівнянням виражається закон Біо−Савар−Лапласа в інтегральній формі, який називають законом повного струму. Вихровий характер магнітного поля

Лінії магнітної індукції неперервні: вони не мають ні початку, ні кінця. Це має місце для будь-якого магнітного поля, викликаного якими завгодно контурами зі струмом. Векторні поля, що володіють безперервними лініями, отримали назву вихрових полів. Ми бачимо, що магнітне поле є вихровий поле. У цьому полягає істотна відмінність магнітного поля від електростатичного.

33. Теорема Гауса для мп

Теорема Гауса — один з основних законів електродинаміки, що входить в систему рівнянь Максвелла.

В системі СІ теорема Гауса має вигляд:

,

де D - вектор електричної індукції,   - сумарний електричний заряд в об'ємі, оточеному поверхнею S:

де   - густина заряду.

В гаусовій системі одиниць СГСГ теорема Гауса формулюється

,

де   - напруженість електричного поля.

Теорема Гауса в диференціальній формі[ред. • ред. Код]

Теорему Гауса можна записати у вигляді диференціального рівняння в часткових похідних, враховуючи формулу Остроградського-Гауса (система СГС):

.

Оскільки це співвідношення справедливе для будь-якого об'єму, рівними повинні бути й підінтегральні вирази:

.

В системі СІ цей вираз має вигляд:

Теорема Гауса для полів у середовищі[ред. • ред. Код]

Теорема Гауса, як одне з основних рівнянь електродинаміки, загалом, справедлива і для середовища, у своїй основній формі. Наприклад, використовуючи систему СГС:

,

якщо під Q розуміти всі заряди, враховуючи мікроскопічні. Однак, присутність зовнішнього заряду призводить до перерозподілу мікроскопічних зарядів у речовині. Тому, якщо внести зовнішній заряд q в діелектрик, то деякі із мікроскопічних зарядів, змістившись, покинуть той об'єм, по якому проводиться інтегрування, інші - увійдуть у цей об'єм зовні - речовина поляризується.

Для врахування цих ефектів в електродинаміці суцільних середовищ усі заряди розділяються на вільні та зв'язані. Вільними вважаються ті заряди, які можна привнести зовні, зяряджаючи тіла, зв'язаними - електричні заряди електронів та ядер речовини, які в зовнішніх полях зміщуються, одні відносно інших, створюючи поляризацію:

,

де   - густина зв'язаних зарядів,   - густина вільних зарядів. Густина зв'язаних зарядів пов'язана з поляризацією:  .

Тоді теорема Гауса записується у вигляді

.

Вводячи вектор електричної індукції

,

отримуємо теорему Гауса для діелектричних середовищ:

,

або в диференціальній формі

.