1.Електричні заряди та їх властивості. Закон збереження електричного заряду.

Існує два види зарядів: позитивно заряджений і негативно.

Позитивно зарядженими називають тіла, які діють на інші заряджені тіла так само, як скло, наелектризоване тертям об шовк.

Негативно зарядженими називають тіла, які діють так само, як ебоніт, наелектризований тертям об хутро.

Зако́н збере́ження електри́чного заря́ду — один із фундаментальних законів фізики. Він полягає в тому, що повний заряд(алгебраїчна сума зарядів) ізольованої замкнутої фізичної системи тіл залишається незмінним при будь-яких процесах, які відбуваються всередині цієї системи.

Для неізольованих систем закон збереження заряду набирає вигляду рівняння неперервності

,

де   - густина заряду,   - густина струму.

Це математичний запис твердження, що зміна густини заряду в достатньо малому об'ємі дорівнює потоку заряду через поверхню цього об'єму (в диференційній формі).

2.Взаємодія електричних зарядів. Сила Кулона. Умови застосування закону Кулона

Взаємодiя зарядiв. Закон Кулона

П ерший кількісний закон взаємодій між елекрично-зарядженими тілами встановлено Шарлем Кулоном у 1780 році. Цей закон справедливий для точкових заряджених тіл. Кулон скористався крутильними терезами, спираючись при цьому на геніальну здогадку, що при контакті зарядженої кульки з незарядженою − заряд між ними розподілиться порівну. Таким чином Кулону вдалось легко поділити початковий заряд на нерухомій кульці в 2, 4, 8, 16 і т.д. разів.

Вимірюючи величину сили взаємодії між зарядами за кутом закручування пружньої дротини, Ш. Кулон встановив кількісний закон: сили взаємодії двох точкових заряджених тіл прямо пропорційні добуткові величини їх зарядів, обернено пропорційні квадратові відстані між зарядами, залежать від природи середовища та напрямлені вздовж лінії центрів тіл:

де, k − коефіцієнт пропорційності, який залежить від вибору системи одиниць вимірювання та для системи СІ дорівнює   (тут ε₀ − має зміст діелектричної проникності вакууму, має розмірність [ε₀]=[Кл²/(Н·м²]);

 − одиничний вектор, напрямлений вздовж вектора   (рис.1);

ε − відносна діелектрична проникність середовища (це число, яке показує у скільки разів сила взаємодії двох точкових зарядів у даному середовищі менша, ніж у вакуумі).

Одиницею заряду в системі СІ є 1 Кл − це кількість електрики, що переноситься зарядженими частинками через переріз провідника за одну секунду при силі струму в 1 А, тобто [1 Кл] = [1 А·1 с].

  3.Напруженість ЕСП. Напруженість точкового заряду . Умова однорідності ЕСП.

Постійне електростатичне поле (ЕСП) — це поле нерухомих електричних зарядів, що здійснює взаємодію між ними.

ЕСП характеризується напруженістю (Б).

Напруженість ЕСП — це відношення сили, що діє в полі на точковий електричний заряд, до величини цього заряду. Одиницею виміру напруженості ЕСП є вольт на метр (В/м).

ЕСП створюється в енергетичних установках і при електротехнічних процесах. Залежно від джерела утворення вони можуть існувати у вигляді власного електростатичного поля (поля нерухомих зарядів) або стаціонарного електричного поля (електричне поле постійного струму).

Напруженість електричного поля у будь-якій точці поля − це відношення сили, що діє на пробний заряд до величини цього заряду: 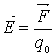  . Звідси слідує, що коли пробний заряд   внести в електричне поле напруженістю   , то на нього буде діяти сила, величиною F=q₀·Е.

Остання формула справедлива для обрахування сили, що діє з боку поля на довільний електричний заряд. При цьому вектори   та   збігаються за напрямком, коли q>0 та мають протилежні напрямки, якщо q <0.

За одиницю напруженості в СІ взято напруженість у такій точці поля, де на пробний заряд величиною в 1 Кл діє сила в 1 Н, тобто [E] = [1 Н/Кл].

В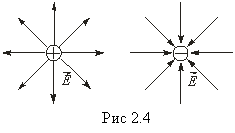 раховуючи із закону Кулона, що  напруженість електричного поля навколо точкового заряду q на довільній відстані rвід нього можна розрахувати як:  .

Для графічного зображення електричних полів користуються методом ліній напруженості − це криві, проведені в електричному полі, дотичні до яких в кожній точці збігаються з напрямком вектора напруженості. Лініям напруженості приписують напрямок, що збігається з напрямком вектора напруженості   . Вважають, що лінії напруженості завжди починаються на поверхні позитивного заряду і закінчуються на поверхні негативного − вони є незамкнутими лініями. Якщо   у всіх точках поля мають однакове значення і напрямок, при цьому лінії напруженості мають рівну густину та паралельні між собою, то поле називають однорідним. Прикладом такого поля може бути електричне поле в зазорі між пластинами конденсатора, хоча вже на краях пластин це поле − неоднорідне (рис.2.6 ). Прикладом неоднорідних полів є й поля навколо точкових зарядів.

4. Силові лінії ЕСП та їх властивості.

Повне уявлення про розподіл поля можна дістати з рисунка, на якому зобразити вектори напруженості, а також показати неперервні лінії, дотичні до яких в кожній точці, через яку вони проходять, збігаються з вектором напруженості. Ці лінії називаються силовими лініями або лініями напруженості (рис.4.1.7). Силові лінії можна зробити видимими, якщо довгасті кристалики діелектрика, наприклад, хініну (ліків від малярії) добре перемішати у в'язкій рідині (рициновій олії) і помістити туди заряджені тіла; поблизу цих тіл кристалики "вишикуються" в ланцюжки вздовж ліній напруженості.

Зобразимо поле різних тіл (рис. 4.1.8 - 4.1.11).

Силові лінії електричного поля точкових зарядів незамкнені. Вони починаються на позитивних електричних зарядах і закінчуються на негативних (рис. 4.1.8 - 4.1.11). Віддалік від країв пластин силові лінії паралельні: електричне поле однакове у всіх точках (рис. 4.1.11).

Електричне поле, напруженість якого однакова у всіх точках простору, називають однорідним.

5. Принцип суперпозиції характерний тим, що він зустрічається в багатьох розділах фізики. Це деякий положення, яке застосовується при ряді випадків. Це один із загальних фізичних законів, на яких будується фізика, як наука. Цим він і примітний для вчених, які застосовують його в різних ситуаціях.

Якщо розглянути принцип суперпозиції в найзагальнішому сенсі, то згідно з ним, сума впливу зовнішніх сил, що діють на частинку, буде складатися з окремих значень кожної з них.

Даний принцип застосовується до різних лінійним системам, тобто таким системам, поведінка яких можна описати лінійними співвідношеннями. Прикладом може послужити проста ситуація, коли лінійна хвиля поширюється в якійсь певній середовищі, в цьому випадку її властивості будуть зберігатися навіть під дією збурень, що виникають через самої хвилі. Ці властивості визначаються як конкретна сума ефектів кожної з гармонійних складових.

Сфери застосування

Як вже було сказано, принцип суперпозиції має досить широкі сфери застосування. Найбільш яскраво його дію можна побачити в електродинаміки. Проте важливо пам'ятати, що розглядаючи принцип суперпозиції, фізика не вважає його конкретним постулатом, а саме наслідком з теорії електродинаміки.

Наприклад, в електростатики даний принцип діє при вивченні електростатичного поля. Система зарядів у конкретній точці створює напруженість, яка буде складатися з суми напруженостей полів кожного з заряду. Даний висновок використовується на практиці, тому що з його допомогою можна порахувати потенційну енергію електростатичного взаємодії. У цьому випадку потрібно буде підрахувати потенційну енергію кожного окремого заряду.

Це підтверджується рівнянням Максвелла, яке лінійно у вакуумі. Звідси також випливає той факт, що світло не розсіюється, а поширюється лінійно, тому окремі промені не взаємодіють один з одним. У фізиці це явище часто називають принципом суперпозиції в оптиці.

Варто також відзначити, що в класичній фізиці принцип суперпозиції випливає з лінійності рівнянь окремих рухомих лінійних систем, тому є наближеним. Він грунтується на глибоких динамічних принципах, але наближеність робить його не універсальним і не фундаментальним.

Зокрема сильне гравітаційне поле описується іншими рівняннями, нелінійними, тому і принцип не може застосовуватися в даних ситуаціях. Макроскопічне електромагнітне поле також не підкоряється даному принципу, тому що залежить від впливу зовнішніх полів.

Однак принцип суперпозиції сил є фундаментальним в квантовій фізиці. Якщо в інших розділах він застосовується з деякими похибками, то на квантовому рівні працює досить точно. Будь квантомеханические система зображується з хвильових функцій і векторів лінійного простору, і якщо вона підпорядковується лінійним функціям, то її стан визначається за принципом суперпозиції, тобто складається з суперпозиції кожного стану і хвильової функції.

Межі застосування досить умовні. Рівняння класичної електродинаміки лінійні, але це не є основним правилом. Більшість фундаментальних теорій фізики будуються за нелінійним рівнянням. Це означає, що в них принцип суперпозиції виконуватися не буде, сюди можна віднести загальну теорію відносності, квантову хромодинаміки, а також теорію Янга-Міллса.

У деяких системах, де принципи лінійності застосовні тільки почасти, може умовно застосовуватися і принцип суперпозиції, наприклад, слабкі гравітаційні взаємодії. Крім того, при розгляді взаємодії атомів і молекул принцип суперпозиції також не зберігається, цим пояснюється різноманітність фізичних і хімічних властивостей матеріалів. цип суперпозиції електричних полів та приклади його застосування.

6.Індукція ЕСП.Потік вектора індукції.Теорема Остроградського-Гауса.

Слово «індукція» походить від латинського кореня, який означає наведення.

На заряд у суцільному середовищі з боку інших зарядів діють сили відмінні від сил у вакуумі. Причиною цього є поляризація середовища. Будь-який матеріал складається із електронів і йонів, які під дією зовнішнього поля зміщуються. В результаті ці наведені заряди створюють свої поля, згідно з принципом Лешательє-Брауна, реакція будь-якої системи на зовнішній влив намагається зменшити ефект цього впливу. Електричне поле, яке діє на пробний заряд з боку інших зовнішніх зарядів менше, ніж у випадку відсутності середовища.

Напруженість електричного поля, розрахована без врахування наведених зарядів і поляризації, й називається вектором електричної індукції у системі СГС. В системі СІ вектор електричної індукції визначений із іншою розмірністю, ніж розмірність напруженості електричного поля, а тому результат розрахунку потрібно ще помножити на   — діелектричну проникність вакууму.

Формулу (8.15) можна узагальнити і на випадок, коли поле створене системою точкових зарядів q₁, q₂,…, q_n. Урахувавши принцип суперпозиції електричних полів, дістанемо

Отже, потік вектора електричної індукції через довільну замкнену поверхню не залежить від діелектричних властивостей середовища і дорівнює алгебраїчній сумі електричних зарядів, що містяться всередині цієї поверхні. Отриманий результат називають теоремою Остроградського — Гаусса.

Теорему Остроградського — Гаусса застосовують для розрахунку індукції (або напруженості) полів, які створюються довільним зарядом, оскільки будь-який заряд можна подати у вигляді суми нескінченно великої кількості точкових зарядів.

Електричний потік (Electric Flux)- потік вектора електричної індукції ( ) через поверхню   (не обов'язково замкнуту).

Відомо, що напруженість електричного поля   залежить від властивостей фізичного середовища, в якому діє електричне поле ( ). Тому для повної характеристики електричного поля вводиться фізична величина, котра має назву електричної індукції (абоелектричного зміщення).

У випадку слабких^[1] електричних полів, відсутності анізотропії та дисперсії, вектор електричної індукції та напруженість електричного поля зв'язані формулою:

,

де  - діелектрична стала. Очевидно, що електрична індукція є векторна величина, що не залежить від властивостей середовища (оскільки останні просто входять в неї):

.

Електричний потік вектора електричної індукції   через довільну поверхню   в певній точці визначається через одиничний вектор нормалі   до цієї поверхні в цій точці:

Звичайно, ця формула справедлива у випадку плоскої поверхні  . В загальному випадку довільної поверхні необхідно брати інтегральний вираз для потоку вектора електричної індукції:

.

7.Потік вектора напруженость ЕСП.Теорема Остроградського-Гауса.

Формулу (8.15) можна узагальнити і на випадок, коли поле створене системою точкових зарядів q₁, q₂,…, q_n. Урахувавши принцип суперпозиції електричних полів, дістанемо

Отже, потік вектора електричної індукції через довільну замкнену поверхню не залежить від діелектричних властивостей середовища і дорівнює алгебраїчній сумі електричних зарядів, що містяться всередині цієї поверхні. Отриманий результат називають теоремою Остроградського — Гаусса.Теорему Остроградського — Гаусса застосовують для розрахунку індукції (або напруженості) полів, які створюються довільним зарядом, оскільки будь-який заряд можна подати у вигляді суми нескінченно великої кількості точкових зарядів.

Потоком вектора напруженості будемо називати величину

  або   ,

де   – проекція вектора   на напрямок вектора нормалі, а вектор  .

Повний потік вектора напруженості через довільну поверхню S буде

.

Знак потоку залежить від вибору напрямку нормалі. Для замкнених поверхонь нормаль, яка виходить назовні, прий­мається за додатну. Тоді там, де вектор   напрямлений назовні,   та   додатні, а коли   входить в середину поверхні,   та   від’ємні (рис. 107).

Для замкнених поверхонь

.

Нехай навколо точкового заряду   який знаходиться у вакуумі, описано довільну замкнену поверхнюS (рис. 108).

Лінії напруженості виходять з цієї поверхні. Виділимо довільну елементарну площадку dS, нормаль   до якої складає кут   з вектором  . Спроектуємо елемент dS поверхні S на поверхню радіуса r з центром в місці знаходження заряду q.Тоді

 

8. ЕСП рівномірно зарядженої частини

Важливим прикладом системи зарядів є заряджена площину. В якості нескінченної площини ми можемо розглядати будь-яку плоску пластину, якщо відстань від точки, в якій шукається поле, до пластини багато менше розмірів самої пластини. Заряджена площину характеризується величиною поверхневої щільності заряду. Що це таке? Візьмемо невелику ділянку площині площею S. Нехай заряд цієї ділянки дорівнює q. Тоді поверхнева щільність заряду визначається як відношення заряду до площі. Іншими словами, поверхнева щільність заряду – це заряд одиниці площі. Поверхнева щільність заряду може мінятися від дільниці до дільниці. Але якщо на будь-якій ділянці площині поверхнева щільність заряду однакова (а = const, т. Е. Заряд розподілений рівномірно), то площина називається рівномірно зарядженою. Вектор напруженості поля рівномірно зарядженої площини перпендикулярний площині; він спрямований від площини, якщо площина заряджена позитивно, і до площини, якщо площина заряджена негативно Приклад зарядженої площини важливий тому, що ми зустрічаємося тут з поняттям однорідного поля. Електричне поле в даній області простору називається однорідним, якщо вектор напруженості поля однаковий в кожній точці області. Іншими словами, напруженість поля в кожній точці розглянутій області має одне й те ж напрямок і незмінну величину. Поле точкового заряду, наприклад, не є однорідним. Справді, напруженість поля точкового заряду може змінюватися від точки до точки як за величиною, так і за напрямком (вона обернено пропорційна квадрату відстані до заряду і спрямована вздовж прямої, що з’єднує заряд з точкою спостереження). А ось заряджена площина створює однорідне електричне поле в кожному з напівпросторів, на які вона розбиває простір. Напруженість цього поля обчислюється за формулами (3.6) або (3.7). ЕСП двох паралельних пластин

Для встановлення кількісних закономірностей поля в діелектрику внесемо в однорідне зовнішнє електростатичне поле, яке створюється двома нескінченними паралельними різнойменно зарядженими пластинами, пластину з однорідного діе­лектрика (рис. 127).

Під дією поля діелектрик поляризується, тобто відбувається зміщення зарядів. Внаслідок цього на правій грані діе­лектрика буде надлишок позитивного заряду з поверхневою густиною  , на лівій – від’ємного заряду з поверхневою густиною  . Ці нескомпенсовані заряди, що появляються внаслідок поляризації діелектрика, називаються зв’язаними. Ос­кільки їх поверхнева густина   менша від густини   вільних зарядів площин, то не все поле   компенсується зарядами діе­лектрика: на границі діелектрика відбувається розрив ліній напруженості зовнішнього електричного поля. Отже, поляризація діелектрика викликає зменшення в ньо­му поля порівняно з початковим зовнішнім полем. Поза діелектриком  . Поява зв’язаних зарядів приводить до виникнення електричного поля  , яке ослаблює  . Результуюче поле всередині діелек­трика:

.

Оскільки поля   і   створені двома нескінченними зарядженими площинами, то

   і    .

Тому результуюче поле

.

Отже, напруженість поля при наявності діелектрика обчислюється за такою ж формулою, як і для вакууму з тією лише відмінністю, що до вільних зарядів треба додати зв’язані заряди протилежного знака.

9. потенціал ЕСП. Потенціальна енергія заряду в ЕСП. Робота сил поля з переміщення заряду

З погляду теорії близькодії на заряд безпосередньо діє електричне поле, створене іншим зарядом. Під час переміщення заряду, діюча на нього з боку поля сила виконує роботу. Тому можна стверджувати, що заряджене тіло в електричному полі має енергію.

Розглянемо дві пластинки, розміщені вертикально. Ліва пластинка В заряджена негативно, а права С - позитивно (рис. 4.1.14). Обчислимо роботу, що виконується полем А під час переміщення заряду q із точки 1, яка знаходиться на відстані d₁ від пластини В, у точку 2, розміщену на відстані d₂ < d₁ від тієї ж пластинки. Точки 1 і 2 лежать на одній силовій лінії.

На ділянці шляху Dd = d₁ - d₂ електричне поле виконує додатну роботу:

A = qE(d₁ - d₂) = - (qEd₂ - qEd₁).                    

Оскільки ця робота не залежить від форми траєкторії, то вона дорівнює зміні потенціальної енергії, взятій з протилежним знаком:

A = - (W_p2 - W_p1) = - DW_p.                           

Порівнюючи рівняння бачимо, що потенціальна енергія заряду в однорідному електричному полі

W_p = qEd,

де заряд q може бути і позитивним, і негативним.

На замкненій траєкторії, коли заряд повертається в початкову точку, робота поля дорівнює нулю:

A = DW_p = - (W_p2 - W_p1) = 0.

Поля, що мають цю властивість, називають потенціальними (гравітаційні, електростатичні).

Потенціальна енергія в електростатичному полі пропорційна заряду, тому відношення W_p до q не залежить від вміщеного в поле заряду. Це дозволяє ввести нову кількісну характеристику поля - потенціал - відношення потенціальної енергії до заряду:

,

[φ] = В = Дж/Кл.

Потенціал - скалярна фізична величина, що є енергетичною характеристикою електричного поля і визначає потенціальну енергію заряду q в довільній точці електричного поля.

Потенціал поля в даній точці рівний тій роботі, яку виконає поле переміщуючи одиничний заряд з даної точки в нескінченність, тобто туди, де поля немає 

 Потенціал однорідного поля

.

В загальному випадку, якщо поле неоднорідне

Е(r)=-φ(r)' 

тобто функція залежності  напруженості поля від відстані є похідною від функції потенціалу, взтій з знаком "мінус". Знак тут вказує на те, що вектор напруженості направлений завжди в сторону зменшення потенціалу 

Потенціал поля точкового заряду

.

Потенціал в довільній точці поля визначають як суму потенціалів, створених окремими точковими зарядами:

j = j₁ + j₂ + … + j_n.

Практичне значення має не сам потенціал, а його зміна. Оскільки W_p = qj, то робота

A = - (W_p2 - W_p1) = - q(j₂ - j₁) = q(j₁ - j₂) = qU,

де U = (j₁ - j₂) - різниця потенціалів або напруга. Вона дорівнює:

U = (j₁ - j₂) =  .

Різниця потенціалів або напруга між двома точками - це фізична скалярна величина, що дорівнює відношенню роботи поля, яка виконується для переміщення заряду із початкової точки поля в кінцеву, до величини цього заряду.

Напруга вимірюється у СІ у вольтах (В):

.

Напруга U = 1 В, якщо під час переміщення заряду в 1 Кл із однієї точки в іншу поле виконує роботу в 1 Дж.

Знаючи потенціал в кожній точці поля, можна знайти напруженість поля. Між напруженістю електростатичного поля E і напругою існує зв'язок. Оскільки A = qEDd і A = qU, то у разі рівності лівих частин рівними будуть і праві частини цих формул. Отже, звідси

.                 

Ця формула показує:

1) чим менше змінюється потенціал на відстані Dd, тим меншою є напруженість електричного поля;

2) якщо потенціал не змінюється, то напруженість дорівнює нулю;

3) напруженість електричного поля напрямлена в бік зменшення потенціалу.

Виходячи з формули (4.1.11), одиницею напруженості буде:

.

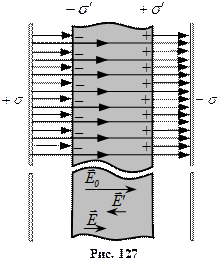
Під час переміщення заряду під кутом 90° до силових ліній електричне поле не виконує роботу, оскільки сила перпендикулярна до переміщення, а це означає, що всі точки поверхні, перпендикулярної до силових ліній, мають однаковий потенціал. Поверхні однакового потенціалу називають еквіпотенціальними. Еквіпотенціальні поверхні однорідного поля єплощинами (рис.4.1.15), а поля точкового заряду - концентричними сферами (рис.4.1.16).

.

Силові лінії, так само, як і еквіпотенціальні поверхні, якісно характеризують розподіл поля в просторі. Вектор напруженості електричного поля перпендикулярний до еквіпотенціальних поверхонь. Еквіпотенціальною є будь-яка поверхня провідника в електростатичному полі.

10. взаємна енергія системи зарядів

Нагадаємо, що потенціал точкового заряду на деякій відстані r математично описується виразом.   , а потенціал, це робота з переміщення заряду в потенціальному полі, тобто   .

Взаємну потенціальну енергію двох зарядів визначають із співвідношення  . Якщо система складається із N точкових зарядів q₁, q₂, …, q_N,, то енергія взаємодії такої системи буде дорівнювати сумі енергій взаємодій зарядів, взятих попарно, тобто   . Оскільки 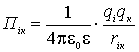  , то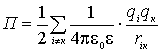  . В останній формулі індекси і та к пробігають незалежно одне від іншого всі значення від 1 до N, не враховуючи значення, де і=к, отже, останню формулу можна подати у вигляді   . У цьому виразі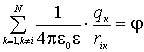  − є потенціалом, що задають всі заряди, крім q_i в тій точці, де розміщений заряд q_i. Тоді й маємо, що   (1).

Нескладно описати й енергію зарядженого провідника, для цього будемо розглядати його, як систему точкових елементарних зарядів q_i. Оскільки поверхня провідника еквіпотенціальна, то потенціали точок, в яких знаходяться точкові заряди q_i, однакові і дорівнюють потенціалу провідника φ.

Користуючись (1), можемо записати:   , де q − сумарний заряд провідника. Пам’ятаючи, що ємність     .

Визначимо енергію зарядженого конденсатора. Нехай потенціал пластини конденсатора, на якій знаходиться заряд +Q дорівнює φ₁, а потенціал пластини, на якій знаходиться заряд −Q − φ₂. Це значить, що кожен із елементарних зарядів q_i, які складають заряд +Q знаходяться в точках із потенціалом φ₁, відповідно, кожен із елементарних зарядів, що складають заряд −Q, розташовані в точках з потенціалом φ₂. Відповідно до формули (1) енергія такої системи зарядів буде дорівнювати

 ,

або скориставшись співвідношенням між електроємністю, потенціалом та зарядом, одержимо:   .

  11. еквіпотенціальні поверхні та лінії

Уявна поверхня, всі точки якої мають однаковий потенціал називаютьсяеквіпотенціальними поверхнями. Їх рівняння мають вигляд:

φ(x, y ,z)=const.

При переміщенні по еквіпотенціальній поверхні на dl потенціал φ не змінюється (dφ=0). Тоді дотична до поверхні складова вектора напруженості дорівнює нулю. Отже, вектор напруженості в кожній точці направлений по нормалі до еквіпотенціальної поверхні, яка проходить через дану точку. Звідси, лінії напруженості в кожній точці ортогональні до еквіпотенціальної поверхні.

Еквіпотенціальну поверхню можна провести через будь-яку точку поля, тоді таких поверхонь може бути безліч. Проводять такі поверхні таким чином, щоб різниця потенціалів для двох сусідніх поверхонь була всюди одна і та ж сама. В такому випадку, по густині еквіпотенціальних поверхонь можна судити про величину напруженості поля. Чим густіше розташовані еквіпотенціальні поверхні, тим швидше змінюється потенціал при переміщенні вздовж нормалі до поверхні, відповідно, тим більше в даному місці   і Е.

 Для однорідного поля еквіпотенціальні поверхні представляють собою систему рівновіддалених одна від одної площин, перпендикулярних до напрямку поля.

Для точкового заряду еквіпотенціальні поверхні можна представити у вигляді, показаному на рис.1.5.

Рис.1.6

1.7. Електричний диполь

Електричним диполем називається система двох однакових за величиною різнойменних точкових зарядів +q і –q, відстань l між якими значно менша відстані до тих точок, в яких визначається поле системи. Пряма, яка проходить через обидва заряди називається віссю диполя; l – плече диполя.

Поле диполя має осьову симетрію. Якщо відстань між зарядами не змінюється, то такий диполь називається жорстким. Якщо довжина плеча диполя l мала порівняно з відстанню r до точки спостереження, то такий диполь називаєтьсяточковим.

 Основною характеристикою електричного диполя є його електричний дипольний момент р – вектор, який чисельно дорівнює добуткові заряду на плече і направлений від негативного заряду до позитивного.

 .

12. що таке градієнт фізичної величини. Чому дорівнює градієнт потенціалу?

Градіє́нт, Ґрадіє́нт — міра зростання або спадання в просторі якоїсь фізичної величини на одиницю довжини.

Для позначення градієнта використовується оператор Гамільтона  , або оператор  .

Градієнт, як завжди вважають, — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Але при замінах координат, градієнт перетворюється інакше, ніж вектор, і тому його не можна розглядати як справжній вектор.

Для скалярного поля   градієнт визначається формулою

де  ,  ,   — орти системи відліку.

Це означення узагальнюється на простори будь-якої розмірності

.

Приклади[ред. • ред. код]

Градієнт скалярного поля[ред. • ред. код]

Градієнт скалярного поля (рос. градиент скалярного поля, англ. gradient of scalar field, нім. Skalarfeld-Gradient m) — вектор, проекціями якого на координатні осі є частинні похідні функції, яка описує дане поле. Практичне тлумачення полягає в тому, що він визначає напрям, у якому задане скалярне поле змінюється найшвидше.

Градієнт тиску[ред. • ред. код]

Градієнт тиску (рос. градиент давления; англ. pressure gradient; нім. Druckgradient m, Druckgefälle n) — втрата тиску на одиниці довжини шляху руху рідини (газу).

Градієнт метановості вугільних шахт[ред. • ред. код]

Градієнт метановості вугільних шахт (рос. градиент метанообильности угольных шахт, англ. gradient of methane content of coal-mine, нім. Methanmengegradient m in den Grubenbauen) — приріст середньої відносної газовості вугільних шахт при зануренні гірничих робіт в зону метанових газів. Здебільшого вимірюється в м³/т при заглибленні на 1 або 100 м.

Оскільки електростатичне поле є потенційним робота з переміщення заряду в такому полі може бути представлена, як різниця потенційних енергій заряду в початковій і кінцевої точках шляху. (Робота дорівнює зменшенню потенційної енергії, або зміні потенційної енергії, узятому зі знаком мінус.)

 

Постійну визначають із умови, що при видаленні заряду q₀ на нескінченність його потенційна енергія повинна дорівнювати нулю.

.

Різні пробні заряди q_0i, поміщені в дану точку поля будуть мати в цій точці різні потенційні енергії:

    … 

 

Відношення W_{пот i}  до величини пробного заряду q_0i, поміщеного в дану точку поля є величиною постійною для даної точки поля для всіх пробних зарядів. Це відношення називається ПОТЕНЦІАЛОМ.

ПОТЕНЦІАЛ – енергетична характеристика електричного поля. ПОТЕНЦІАЛ чисельно дорівнює потенційної енергії, якої має в даній точці поля одиничний позитивний заряд.

Роботу з переміщення заряду можна представити у вигляді

.

Потенціал виміряється у Вольтах

ЕКВІПОТЕНЦІАЛЬНИМИ ПОВЕРХНЯМИ називаються поверхні рівного потенціалу (φ = const). Робота з переміщення заряду уздовж еквіпотенціальної поверхні дорівнює нулю.

Зв'язок між напруженістю   й потенціалом φ можна знайти, виходячи з того, що роботу з переміщення заряду q  на елементарному відрізку  d? можна представити як

                                       

З іншої сторони                               

 - градієнт потенціалу

Напруженість поля дорівнює градієнту потенціалу, узятому зі знаком мінус.

Градієнт потенціалу показує, як міняється потенціал на одиницю довжини. Градієнт перпендикулярний функції й спрямований убік зростання функції. Отже, вектор напруженості перпендикулярний еквіпотенціальної поверхні й спрямований убік убування потенціалу.

Розглянемо поле, створюване системою N точкових зарядів q₁, q₂, … q_n. Відстані від зарядів до даної точки поля рівні  r₁, r₂, … r_n. Робота, чинена силами цього поля над зарядом q₀, буде дорівнювати алгебраїчній сумі робіт сил, кожного заряду окремо.

гле 

 

 

               

Потенціал поля, створюваного системою зарядів, визначається як алгебраїчна сума потенціалів, створюваних у цій же точці кожним зарядом окремо.

 

13.Зв’язок напруженості ЕСП з потенціалом

14. Циркуляція есп. Потенціальний характер есп

Система заряджених тіл, між якими діють центральні кулонівські сили, має запас енергії взаємодії між тілами, яку називають потенціальною.

Під дією кулонівських сил заряджені тіла рухаються з прискоренням і їх кінетична енергія замкнутої системи збільшується лише тоді, коли потенціальна зменшується (і навпаки).

Електростатичне поле створене системою заряджених тіл являється потенціальним. Циркуляція вектора напруженості електростатичного поля дорівнює нулю.

Крім силової векторної характеристики поля – напруженості для кожної точки поля існує скалярна енергетична характеристика – потенціальна. Між ними існує зв’язок.

Потенціальний характер електростатичного поля. Циркуляція вектора напруженості електростатичного поля

Під час переміщення заряду під дією електростатичного поля виконується робота. Знайдемо роботу, яка виконується під час переміщення точкового заряду   із точки А в точку В у полі точкового заряду q .

Рис. 1

На заряд   з боку q діє кулонівська сила

,

яка залежить від відстані.

Для знаходження роботи розіб’ємо весь шлях АВ на елементарні ділянки dl , де силу можна вважати сталою. Тоді елементарна робота на dl

,

де a – кут між напрямком сили і напрямком переміщення:

 (по рис.).

Зміна відстані заряду   від  ;

Тому  .

Повна робота на всьому шляху знайдеться при інтегруванні від   до  .

.

Отож, з цієї роботи можна зробити висновки:

1. Робота по переміщенню заряду в електростатичному полі не залежить від форми траєкторії руху і визначається тільки кінцевим ( ) і початковим ( ) положенням заряду, (а також від величин зарядів   і q і діелектричної проникності e ). Поля з такими властивостями називаються потенціальними (консервативними). Так чином електростатичне поле – потенціальне.

1. Якщо шлях замкнутій траєкторії можна визначити

,

 – елементарна переміщення.

За означенням

.

Тоді  .

Таким чином  .

Інтеграл по замкнутому контуру   називається циркуляцією вектора напруженості електричного поля.

Силове поле, циркуляція силового вектора якого дорівнює 0, називається потенціальним, консервативним. Таким чином, електростатичне поле потенціальне.

Потенціал. Різниця потенціалів

За законом збереження енергії робота в електростатичному полі виконується за рахунок зменшення потенціальної енергії зарядженого тіла.

При переміщенні заряду   в електростатичному полі заряду q виконується робота:

,

яка дорівнює

.

Якщо заряд   переміщується в нескінченність 

тоді

;  .

Потенціальна енергія заряду на нескінченості вважається рівною 0.

Таким чином заряд   в електростатичному полі зарядуq на відстані r від нього має потенціальну енергію (в системі СІ):

.

Для різних пробних зарядів  і т.д. в одній і тій де точці поля (r = const ) потенціальна енергія різна   і т.д., але відношення потенціальної енергії до відповідних зарядів одне й те саме.

.

Це відношення характеризує певну точку поля називається потенціалом і позначається j .

Потенціалом електростатичного поля в будь-якій його точці називається фізична величина, що дорівнює потенціальній енергії одиничного позитивного заряду, розміщеного в цій точці. ( ).

А також потенціал можна визначити:

Фізична величина, що дорівнює роботі виконуючій силі поля при переміщенні одиничного позитивного заряду із даної точки поля на нескінченність:  .

Очевидно, що ця робота в числовому виразі дорівнює роботі зовнішніх сил проти сил електростатичного поля при переміщенні одиничного позитивного заряду із нескінченності в дану точку поля.

На практиці зручніше приймати рівним 0 потенціал Землі.

Це можливо тому, що при будь-яких розрахунках важливо знати різницю потенціалів між двома точками електростатичного поля, а на їх абсолютне значення.

За одиницю потенціалу в системі СІ приймається В (вольт). Потенціал в один вольт має точка поля, в якій заряд в один кулон має потенціальну енергію в 1 джоуль.

.

Потенціал точкового заряду має вираз:

.

Тоді робота по переміщенню заряду   в електростатичному полі заряду q із точки потенціалом   в точку з потенціалом   визначається

, або 

Таким чином, робота сил електростатичного поля при переміщенні точкового заряду дорівнює добутку величини цього заряду на різницю потенціалів в початковій і кінцевій точках траєкторії:

,

тому різниця потенціалів двох точок електростатичного поля (  вимірюється роботою сил при переміщенні одиничного позитивного заряду між цими точками.

Потенціал, за визначенням, енергетична характеристика електростатичного поля; величина алгебраїчна (скалярна).

Потенціал електростатичного поля системи зарядів в будь-якій точці поля дорівнює алгебраїчній сумі потенціалів кожного точкового заряду.

.

В цьому суттєва перевага скалярної характеристики поля (потенціалу) перед його векторною силовою характеристикою (напруженістю), що дорівнює геометричній сумі складених напруженостей.