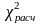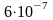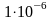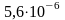5.3. Анализ полученных результатов моделирования.
В результате аналитического моделирования получены интересующие нас вероятностные характеристики системы. При аналитическом моделировании система ПРО рассматривалась в виде графа гибели и размножения, что позволило определить вероятности состояний из системы уравнений. Также эти характеристики могут быть посчитаны по заранее известным формулам. Расчет по этим формулам произведён в программе an_model.pas, листинг которой представлен в Приложении 1. Результаты аналитического моделирования представлены также в Приложении 2. А требуемые графики в Приложении 3.
Проводя моделирование при увеличении числа обслуживающих приборов от 2 до 4, наблюдаем:
увеличение вероятности обслуживания;
уменьшения вероятности занятости канала;
увеличение среднего времени простоя канала.
6. Сопоставление полученных результатов для разработанных моделей.
Что бы убедиться
в адекватности применяемых моделей
СМО, воспользуемся статистическим
критерием
,
который служит для проверки однородности
двух независимых выборок.
Если выборки
однородны, то считают, что они извлечены
из одной генеральной совокупности и,
следовательно, имеют одинаковые, причем
неизвестные, непрерывные функции
распределения
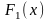и
.
Таким образом,
нулевая гипотеза состоит в том, что при
всех значениях аргумента функции
распределения равны между собой:
Для того чтобы при
заданном уровне значимости
и количестве степеней свободы
проверить нулевую гипотезу
:
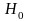об
однородности двух независимых выборок
объемов
и
(
)
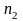при конкурирующей гипотезе
:
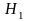необходимо
найти величину
по формуле:
,
и сравнить полученное
значение с табличным
для данных
и
.
Если
,
нулевую гипотезу отвергают.
Если
,
гипотеза об однородности выборок
принимается.
Зададимся уровнем
значимости
(число степеней свободы
),
при объеме выборки
.
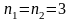Значение для данных параметров равно 0,004.
В качестве выберем вероятность плотность потока обслуженных заявок для аналитической модели, а – для имитационной модели.
Результаты расчетов сведем в таблицу.
|
|
|
0,5336 |
0,5338 |
|
0,7407 |
0,7459 |
|
0,8946 |
0,8912 |
|
|
|
|
Таблица 3. Расчёт значения
Из таблицы получили , поэтому принимаем нулевую гипотезу об однородности выборок. Проведя аналогичные вычисления для среднего времени простоя канала, получили следующие результаты:
Следовательно, выдвинутая гипотеза в этом случае также принимается.
Таким образом, результаты сравнения показывают адекватность моделей.
7. Выводы.
В процессе выполнения данной индивидуальной работы мы познакомились с системами массового обслуживания на примере системы ПРО с отказами и упорядоченным обслуживанием. Данная система ПРО была рассмотрена как система массового обслуживания с отказами и ограниченным временем пребывания заявок в системе.
Для заданной системы были построены две модели: аналитическая модель и имитационная модель. В основе аналитической модели лежит представление работы системы в качестве графа гибели-размножения. По этому графу можно путем решения алгебраической системы уравнений (рассматривается статический режим и пуассоновский поток на входе) можно определить вероятностные характеристики системы – вероятность обслуживания, вероятность занятости канала, среднее время простоя канала и др. Для вычисления этих параметров была написана программа an_model.pas, листинг которой приведён в Приложении 1.
Имитационная модель строилась с учетом всех особенностей функционирования реальной системы и поэтому она достаточно точно описывает все вероятностные процессы. Листинг программы имитационного моделирования также приведён в Приложении 1.
На этапе сравнения двух построенных моделей с помощью критерия были сделаны следующие выводы:
с точки зрения вычисления такой характеристики системы как вероятность отказа модели (аналитическая и имитационная) адекватны.
с точки зрения вычисления среднего времени простоя канала модели - также адекватны.
Также была выявлена зависимость вероятностных характеристик системы от числа обслуживающих приборов, были получены следующие закономерности. Проводя моделирование, при увеличении числа обслуживающих приборов от 2 до 4 наблюдаем:
увеличение вероятности обслуживания;
уменьшения вероятности занятости канала;
увеличение среднего времени простоя канала.
Соответствующие зависимости в виде графиков представлены в Приложении 3.