5. Разработка аналитической модели.

5. 1 Математическое описание аналитической модели

Рассматривается система ПРО с отказами и упорядоченным обслуживанием. Упорядоченное обслуживание состоит в том, что заявки строго распределены по свободным каналам (нет случайного распределения заявок и нет взаимопомощи). С точки зрения СМО рассматриваемая система представляет СМО с отказами в обслуживании и «нетерпеливыми» заявками, когда канал мгновенно освобождается либо при обслуживании заявки (поражение самолёта), либо при уходе заявки из системы (непоражение самолёта)

Рассмотрим работу n – канальной системы ПРО с ограниченным временем пребывания заявки в системе. Алгоритм работы системы следующий: если к моменту поступления заявки в систему свободен хотя бы один из n каналов, то эта заявка принимается к обслуживанию только одним из свободных каналов. Если к моменту поступления заявки в систему все каналы заняты, то данная заявка остаётся необслуженной. На занятый канал действует пуассоновский поток освобождений с интенсивностью . Эта интенсивность является суммой интенсивности потока обслуживаний одного канала и интенсивности потока уходов заявки из под обслуживания .

- интенсивность простейшего входящего потока заявок;

- интенсивность потока обслуживания заявок;

- интенсивность потока освобождения канала;

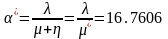
В любой момент времени рассматриваемая система может находиться в одном из следующих состояний:

- в системе нет ни одной заявки (свободны все каналы);

- одна заявка в системе и она обслуживается одним (любым) из n каналов;

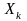- ровно заявок в системе и все они обслуживаются (каждая заявка одним каналом);

- ровно n заявок в системе обслуживается n каналами.

Этой системе соответствует граф состояний:

За состояние принимается загрузка канала обслуживания заявки.

Так как система пуассоновского типа, то . Поэтому можно записать систему алгебраических уравнений в общем виде:

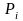- вероятность того, что система находится в состоянии .

Последнее уравнение системы представляет собой условие нормировки, так как мы имеем дело с полной группой событий. Решив данную систему алгебраических уравнений можно найти вероятности нахождения системы в каждом из состояний.

А также вероятности состояний могут быть найдены по следующим формулам:

,

где , и - табличные функции пуассоновского распределения

Интересующие нас характеристики определяются следующим образом:

1. Плотность потока обслуженных заявок

2. Среднее число занятых каналов

.

3. Вероятность занятости канала

.

4. Среднее время простоя канала

5. Среднее время занятости канала (по условию оно распределено по показательному закону с параметром ). Следовательно, среднее время занятости будет

Расчет по этим формулам произведён в программе аналитического моделирования

5.2. Расчёт параметров смо.

Рассчитаем параметры системы по графу состояний СМО.

1. Запишем граф состояний и систему уравнений для двухканальной СМО ( ).

Система будет иметь 3 состояния:

1. X₀ – нет заявок на обслуживании;

2. X₁ – 1 заявка на обслуживании;

3. X₂ – 2 заявки на обслуживании;

Граф состояний имеет вид:

Этому графу соответствует система алгебраических уравнений, которую необходимо решить для получения интересующих параметров.

Программа для расчёта требуемых параметров приведена в Приложении 1:

Определим требуемые параметры:

Плотность потока обслуженных заявок:

Вероятность занятости канала:

Среднее время простоя канала:

2. Запишем граф состояний и систему уравнений для трёхканальной СМО ( ).

Система будет иметь 4 состояния:

4. X₀ – нет заявок на обслуживании;

5. X₁ – 1 заявка на обслуживании;

6. X₂ – 2 заявки на обслуживании;

7. X₃ – 3 заявки на обслуживании;

Граф состояний имеет вид:

Этому графу соответствует система алгебраических уравнений, которую необходимо решить для получения интересующих параметров.

Программа для расчёта требуемых параметров приведена в Приложении 1:

Определим требуемые параметры:

Плотность потока обслуженных заявок:

Вероятность занятости канала:

Среднее время простоя канала:

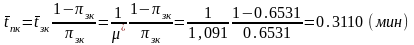
3. Запишем граф состояний и систему уравнений для четырёхканальной СМО ( ).

В этом случае система будет иметь 5 состояний.

Граф состояний имеет вид:

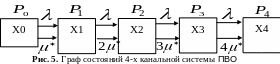
Этому графу соответствует система алгебраических уравнений, которую необходимо решить для получения интересующих параметров.

Определим требуемые параметры:

Плотность потока обслуженных заявок:

Вероятность занятости канала:

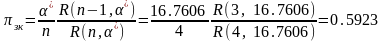
Среднее время простоя канала:

Число каналов обслуживания,	Искомый параметр	Аналитическая модель
		0,5338
		0.7131
		0.2400
		0,7459
		0.6531
		0.3110
		0,8912
		0.5923
		0.3417

Таблица 2. Результаты аналитического моделирования