4. Разработка имитационной модели.
4.1. Математическое описание имитационной модели.
Имитационное моделирование основано на искусственной реализации вероятностных законов. С помощью генератора вырабатываются независимые реализации случайного процесса. Интересующие нас характеристики находятся путём усреднения по множеству реализаций.
Приведём построение имитационной модели для заданной СМО.
Исходные данные для имитационной модели:
Дисциплина обслуживания - СМО с отказами и упорядоченным обслуживанием.
- число каналов обслуживания;
- интенсивность простейшего входящего потока заявок;
Интенсивность потока обслуживания заявок;
(час-1)
≈5,3(мин-1)
(мин-1)
- интенсивность простейшего потока освобождения канала;
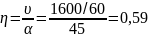(мин-1)
(мин-1)
Интенсивности поступления и обслуживания заявок распределены по пуассоновскому закону.
При разработке
имитационной модели для реализации
входного потока заявок и потока
обслуживания из равномерной случайной
величины, генерируемой ЭВМ, необходимо
получить случайную величину, распределённую
по пуассоновскому закону. Пусть
-
случайная величина, равномерно
распределённая в интервале
.
Для пуассоновского распределения примем
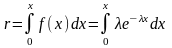
Осуществив интегрирование, получим:
Решая это уравнение
относительно
,
имеем:
.
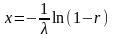Случайное число
распределено равномерно в интервале
,
следовательно
также случайная величина, принадлежащая
интервалу
.
Поэтому
и
распределены одинаково. Отсюда имеем:
.
Определяемая этим соотношением случайная величина имеет пуассоновский закон распределения. Таким образом, интервал времени между заявками определяется следующим образом:
,
где
- случайная величина в диапазоне
,
генерируемая ЭВМ.
Требуемые характеристики СМО можно определить следующим образом:
1) Абсолютная пропускная способность определяется по формуле:
.
где - вероятность обслуживания.
2) вероятность занятости канала:
,
где
-
время занятости
- го канала;
- время моделирования;
- число каналов обслуживания.
3) среднее время простоя канала:
,
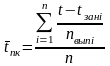где
-
время занятости
- го канала;
- время моделирования;
- число каналов обслуживания;
- количество заявок, выполненных
- тым каналом за время моделирования.
Таким образом, используя имитационную модель можно получить требуемые параметры.
Имитационное моделирование включает следующие этапы:
1. Построение входного потока заявок. Время появления заявки определяется следующим образом:
,
где
- модельное время.
2. Обслуживание заявок. Для каждой заявки, стоящей на обслуживании, проверяется, не истекло ли время её обслуживания. Если время истекло, то заявка считается обслуженной и занятые ей приборы освобождаются.
3. Генерация новой заявки. Генерируется время выполнения пришедшей заявки, т.к. оно распределено по пуассоновскому закону, то время выполнения:
,
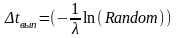где
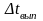- время выполнения пришедшей заявки.
Блок- схема имитационного моделирования приведена в приложении 4. Описание блок-схемы алгоритма приведено ниже.