
437. Теңдеуді шешіңіз: Решить уравнение.
438.
![]() теңдеуін шешу үшін қолданылатын тәсіл:
Чтобы решить уравнение
теңдеуін шешу үшін қолданылатын тәсіл:
Чтобы решить уравнение
![]() надо применить метод:
надо применить метод:
 ауыстыруын
жасау. Сделать замену y=хt
ауыстыруын
жасау. Сделать замену y=хt
 ауыстыруын
жасау. Сделать замену x=yt
ауыстыруын
жасау. Сделать замену x=yt
Айнымалыларын бөліп алу. Разделить переменные
Тұрақтыны түр өзгерту тәсілі. Метод вариации произвольных постоянных
Тікелей интегралдау тәсілі. Применить непосредственное интегрирование.
439.
![]() дифференциалдық теңдеуінің реті неге
тең: Порядок дифференциального уравнения
равен:
дифференциалдық теңдеуінің реті неге
тең: Порядок дифференциального уравнения
равен:
2
9
1
0
3
440. Теңдеуді шешіңіз: Решите уравнение
441. Теңдеуді шешіңіз: Решите уравнение .
442.
![]() функциясы берілген.
функциясы берілген.
![]() -ті
табыңыз. Для функции
частная производная
равна
-ті
табыңыз. Для функции
частная производная
равна
443.
Біртекті
сызықтық
дифференциал
теңдеудің
дербес
шешімінің
түрін
анықтаңыз.
Определить
вид
частного
решения
линейного
неоднoродного
дифференциалного
уравнения
![]()
444.
![]() функциясы берілген.
функциясы берілген.
![]() -ті
табыңыз. Найти
,
функции
-ті
табыңыз. Найти
,
функции
445.
Дифференциал теңдеудің ретін анықтаңыз.
Порядок дифференциального уравнения
![]() равен:
равен:
3
2
1
0
4
446.
![]() функциясы берілген.
-ті
табыңыз.Дана функция
,
найти производные
.
функциясы берілген.
-ті
табыңыз.Дана функция
,
найти производные
.
447.
Біртекті сызықтық дифференциал теңдеудің
дербес шешімінің түрін анықтаңыз.
Определить вид частного решения
линейного неоднородного дифференциального
уравнения
![]()
448.
Теңдеуді шешіңіз. Решите уравнение:
![]()
449.
![]() функциясы берілген.
функциясы берілген.
![]() нүктесіндегі
нүктесіндегі
![]() -ты
есептеңіз: Найдите
в
точке
-ты
есептеңіз: Найдите
в
точке![]() ;
;
2
-4
-8
8
-2
450.
![]() функциясы берілген.
функциясы берілген.
![]() -ты
есептеңіз. Найти
,функции
-ты
есептеңіз. Найти
,функции
451.
![]() функциясы берілген.
-ты
есептеңіз. Для функции
частная производная
равна
функциясы берілген.
-ты
есептеңіз. Для функции
частная производная
равна
452. Дифференциал теңдеудің қайсысы бірінші ретті сызықтық теңдеу болады. Какие из следующих дифференциальных уравнений первого порядка являются линейными:
б) в) ?
б,в
б
а,б
а,в
в
453.
Егер![]() функциясы
біртекті болса, онда оның біртектілік
дәрежесін анықтаңыз. Если функция
однородная, то её степень однородности
равна:
функциясы
біртекті болса, онда оның біртектілік
дәрежесін анықтаңыз. Если функция
однородная, то её степень однородности
равна:
0
2
1
4
-3
454.
![]() функциясы берілген.
функциясы берілген.
![]() -ты
есептеңіз. Дана функция
-ты
есептеңіз. Дана функция
![]() найти производную
найти производную
455. Теңдеуду шешіңіз.Решить дифференциальное уравнение
456.
Берілгені: Дано:![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]()
2y
B)2x
y
2xy
x
457.
Берілгені: Дано:
![]() .
Табыңыз:
Найти:
.
Табыңыз:
Найти:
458.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
459.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]()
6y
0
3
x + y
2x
460. Берілгені: Дано: . Табыңыз: Найти:
y3z – 4
6xy2 - 4
461.
Берілгені: Дано:
 .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]()
462.
Берілгені:
Дано:
 .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]()
2
463.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
464.
Берілгені:
Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
465.
Берілгені: Дано:
![]() .Табыңыз:
Найти:
.Табыңыз:
Найти:
6x + 8y
8y + 12x
3x2 + 8xy – 6
6x - 8y
8x - 6y
466.
Берілгені: Дано:
![]() .Табыңыз:
Найти:
.Табыңыз:
Найти:
6y - 12x
6y +12x
12y - 6x
12y + 6x
4x2 - 12xy
467. Берілгені: Дано: .Табыңыз: Найти:
3x2y2 + y
x2y + 5x
468.
Берілгені: Дано:
![]() .Табыңыз:
Найти:
.Табыңыз:
Найти:
![]()
2xy + 2
469. Берілгені: Дано: .Табыңыз: Найти:
2x3y+2.
470.
Берілгені: Дано:
![]() .Табыңыз:
Найти:
.Табыңыз:
Найти:
2x – y + 3
2y - x – 2
2x – y
2x + 3
2y - x
471. Берілгені: Дано: .Табыңыз: Найти:
2y – x - 2
2x - y + 3
2y – x
2y - 2
2x - y
472.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
2xsin(x - y)
473. Берілгені: Дано: . Табыңыз: Найти:
2xsin(x - y)
474.
Берілгені:
Дано:
![]() .Табыңыз:
Найти:
.Табыңыз:
Найти:
10yx
3x2 + cosx
.
475. Берілгені: Дано: .Табыңыз: Найти:
10yx
3x2 + cosx
–3x2 +10xy
 .
.
476.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
2x2 - 4y2
3x2 -4y2.
477. Берілгені: Дано: . Табыңыз: Найти:
478.
Берілгені: Дано:
![]() .Табыңыз:
Найти:
.
.Табыңыз:
Найти:
.
0
479. Берілгені: Дано: .Табыңыз: Найти:
0
480.
Берілгені:
Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
481. Берілгені: Дано: . Табыңыз: Найти:
482.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
ysin(xy) – e
ycos(xy)+2ex-y.
483.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]() .
.
9
8
10
6
484. функциясының М(1;-2) нүктесіндегі табыңыз: значение выражения в точке М(1;-2):
9
6
1
3
-1
485.
Берілгені:
Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
486. Берілгені: Дано: . Табыңыз: Найти:
487.
Берілгені: Дано:
![]() .
.
Табыңыз:
Найти:
![]() .
.
6у - 12х
6х + 4у
8ху - 6х
-6у2 + 3у3
8ху - 12у + 6у2
488. Берілгені: Дано: .Табыңыз: Найти: .
6x +8y
6х + 4у
8ху - 6х
-6у2 + 3у3
8ху - 12у + 6у2
489.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]()
4
3
6
5
2
490.
Берілгені: Дано:
![]() .
Табыңыз: Найти:
.
Табыңыз: Найти:
![]() .
.
= 14у3 + 6у2 – у
= 21х2у2 – 12ху + 18
491.
Берілгені: Дано:
.
Табыңыз: Найти:
![]() .
.
= 0
= 14ху3
= 14ху3 – 6у2
492.
Теңдеуді шешіңіз: Решите
уравнение:
![]()
493.
Берілгені: Дано:
![]() .
Нүктесіндегі А(0; 1)
.
Нүктесіндегі А(0; 1)
![]() -ті
табыңыз: Найти в точке А(0; 1)
:
-ті
табыңыз: Найти в точке А(0; 1)
:
-
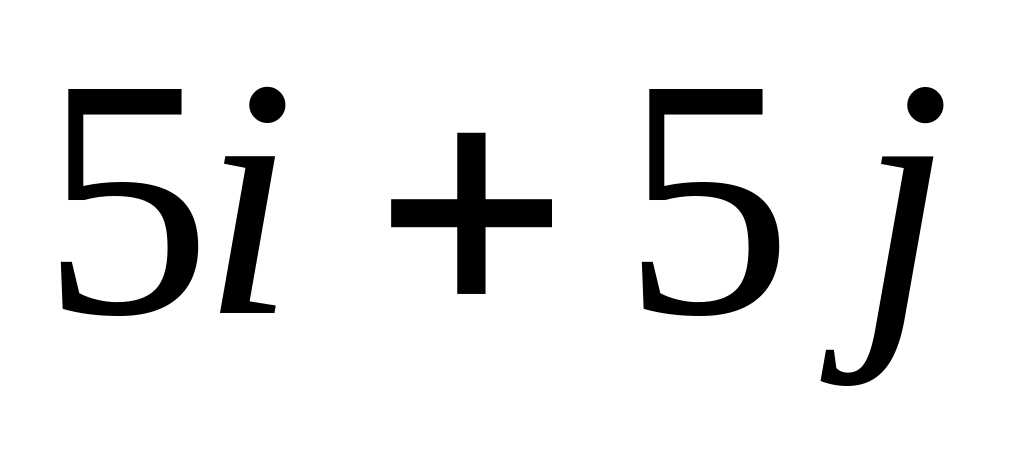

0
-

494.
Дифференциалдық теңдеуінің ретін
табыңыз.Найти порядок дифференциального
уравнения:![]()
1
4
0
3
2
495.
Берілгені: Дано:
![]() .
Нүктесіндегі А(0; 1)
-ті
табыңыз:
.
Нүктесіндегі А(0; 1)
-ті
табыңыз:
Найти в точке А(0; 1) :
496.
Берілгені: Дано:
![]() .
Нүктесіндегі А(0; 1)
-ті
табыңыз:
.
Нүктесіндегі А(0; 1)
-ті
табыңыз:
Найти в точке А(0; 1) :
-

0
-

497.
Теңдеуді шешіңіз: Решите уравнение:
![]()
498.
Теңдеуді шешіңіз: Решите
уравнение:
![]()

2


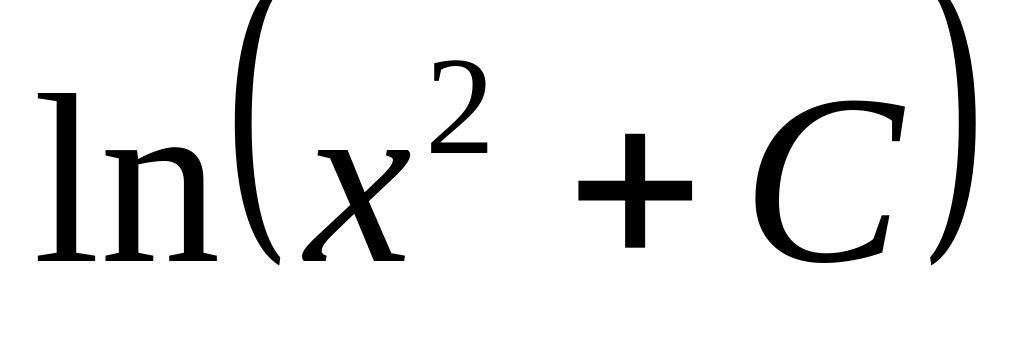

499.
Теңдеуді шешіңіз: Решите
уравнение:
![]() .
.
500.
Теңдеуді шешіңіз: Решите
уравнение:
![]()
