
- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
§ 5. Уравнение линии как множество точек плоскости
Равенство вида
F(x,y)= 0 |
(1) |
называется уравнением с двумя переменными х, у, если это равенство справедливо не для всех пар чисел хиу. Примеры уравнений:
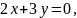
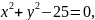
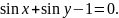
Если (1) справедливо для всех пар чисел х и у то оно называется тождеством. Примеры тождеств:
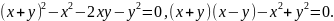
Определение. Уравнение (1) называется уравнением линии L (в заданной системе координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Из определения следует, что линия L представляет собой множество всех тех точек плоскости (х; у), координаты которых удовлетворяют уравнению (1).
Если (1) является уравнением линии L, то говорят, что уравнение (1) определяет (задает) линию L.
Линия L может определяться и уравнением вида
F(ρ,φ)=0,
содержащим полярные координаты.
52.
Даны
точки:
(2;
-2),
(2;
2),
(2;1),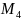 (3;-3),
(3;-3),
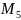 (5;-5),
(5;-5), (3;-2).
Установить, какие из данных точек лежат
на линии, определенной уравнением х +
7=0, и какие из них не лежат на ней.
(3;-2).
Установить, какие из данных точек лежат
на линии, определенной уравнением х +
7=0, и какие из них не лежат на ней.
53.
Установить, какие линии определяются
уравнениями (построить их): 1)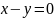 ;
;
2)
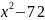 = 0; 3)
= 0; 3)
 ;
4)
;
4)
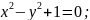
5)
 ,
где
,
где
 и
—
полярные координаты; 6)
а)
и
—
полярные координаты; 6)
а)
 б)
б)
 в)
в)
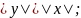 г)
г)
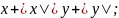 7) a)
7) a)
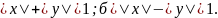
54.
Даны точки
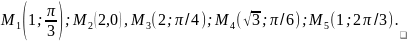 Установить,
какие из данных точек лежат на линии,
определенной уравнением в полярных
координатах
Установить,
какие из данных точек лежат на линии,
определенной уравнением в полярных
координатах
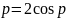 ,
и
какие не лежат на ней.
,
и
какие не лежат на ней.
55. Вывести уравнение множества точек, каждая из которых отстоит от точки С(α, β) на расстоянии R. Иными словами, вывести уравнение окружности радиуса R с центром в точке С (α;β).
56.
Показать, что уравнение
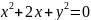 задает на плоскости некоторую окружность.
задает на плоскости некоторую окружность.
57. На плоскости даны точки А и В. Найти множество точек M, удаленных от А вдвое дальше, чем от В.
58.
Установить: а) лежит ли точка N(4,1;
1,9) на окружности с центром С(1; -2) и
радиусом 5; б) лежит ли точка K(0;2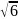 -2)
на этой же окружности; в) лежит ли точка
A(160;
-1)
на окружности с центром (147; -6)
и радиусом 13.
-2)
на этой же окружности; в) лежит ли точка
A(160;
-1)
на окружности с центром (147; -6)
и радиусом 13.
59. Написать уравнение окружности с центром С(-2; 3) н радиусом, равным 5. Известно, что точка А (а; -1) лежит на этой окружности. Найти а.
60. Написать уравнение линии, по которой движется точка М(х; y), равноудаленная от точек А(0; 2) и В(4; -2).
61. Написать уравнение траектории точки M(х; 7), которая при своем движении остается вдвое ближе к точке А(- 1; I), чем к точке B(-4; 4).
62.
Написать уравнение множества точек,
сумма расстояний каждой из которых от
точек F1
(2;
0)
и (-2;
0)
равна 2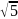 .
.
63. Написать уравнение множества точек, равноудаленных от точки F(2; 2) и от оси Ох.
64. Написать уравнение линии, по которой движется точка М(x; у), оставаясь вдвое дальше от оси Ох, чем от оси Оу.
65. Написать уравнение множества точек, равноудаленных от оси Оу и точки F(4; 0).
66. Написать уравнение линии, по которой движется точка М(х; у), равноудаленная от начала координат и от точки А(-4; 2).
67. Написать уравнение траектории точки М(х; у), которая при своем движении остается вдвое ближе к точке A(0; -1), чем к точке В (0; 4).
