§ 3. Простейшие задачи аналитической геометрии на плоскости

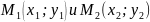1. Расстояние между двумя точками на плоскости

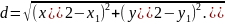
2. Площадь S треугольника ABC с вершинами 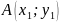, 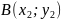и .

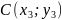
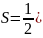3. Деление отрезка в данном отношении. Если точка 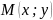делит отрезок с концами и 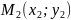в отношении 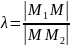, то

В частности, при делении пополам, т.е. в отношении

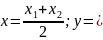
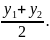
20. Даны точки 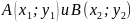. Показать, что формула расстояния между точками А и В не зависит от знаков их координат.

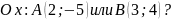21. а) Какая точка дальше от оси б)Какая из этих точек дальше от оси 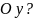в) Чему равны расстояния от точки 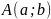до осей 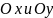соответственно?

22. Даны точки 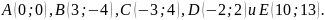Определить расстояние между точками:

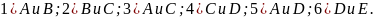
23. Вычислить площадь треугольника, вершинами которого являются точки:

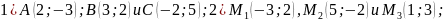
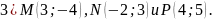
24. Точка М является серединой отрезка ОА, соединяющего начало координат О с точкой

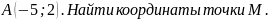
25. Построить точки 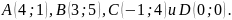Если точки построены правильно, то получен квадрат. Какова его площадь? Чему равна длина стороны этого квадрата? Найти координаты середин сторон квадрата.

26. Площадь треугольника равна 10 кв. ед., две его вершины – точки 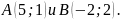Найти координаты третьей вершины, если известно, что она лежит на оси абсцисс.

27. Найти площадь четырехугольника с вершинами в точках

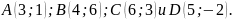
28. Определитель середины сторон треугольника с вершинами

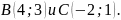
29. Точки 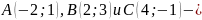середины сторон треугольника. Найти координаты его вершин.

30. Найти координаты центра тяжести однородной пластинки, имеющей форму треугольника с вершинами

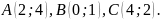
31. Площадь треугольника равна 3 кв. ед., две его вершины – точки 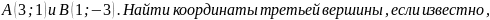что она лежит на оси ординат.

32. Площадь параллелограмма равна 12 кв. ед., две его вершины – точки 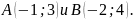Найти две другие вершины этого параллелограмма, если известно, что точка пересечения его диагоналей лежит на оси абсцисс.

33. Вершины треугольника – точки 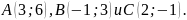Найти длину его высоты, проведенной из вершины C.

34. Три вершины параллелограмма – точки 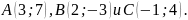Найти длину его высоты, опущенной из вершины В на сторону АС.

35. Отрезок, ограниченный точками 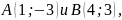разделен на три равные части. Определить координаты точек деления.

36. Определить координаты концов А и В отрезка, который точками

37. Прямая проходит через точки 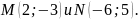Найти на этой прямой точку, ордината которой равна .

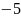38. Прямая проходит через точки 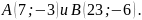Найти точку пересечения этой прямой с осью абсцисс.

39. Три вершины параллелограмма – точки

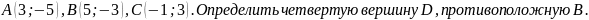
40. На плоскости заданы точки 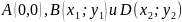(рис. 5). Какие координаты должна иметь точка С, чтобы четырехугольник ABCD был параллелограммом?

Рис.5

§ 4. Полярные координаты

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из нее луча ОЕ называемого полярной осью, и масштаба для измерения длит отрезков.

Пусть задана полярная система координат и пусть М - произвольная точка плоскости. Обозначим через расстояние точки М от точки О, а через (φ — угол, на который нужно повернуть против часовой стрелки полярную ось для совмещения с лучом ОМ (рис. 6).Полярными координатами точки М называются числа ρ и φ. Число ρ называют полярным радиусом, а φ – полярным углом. Символ М(ρ;φ) обозначает, что точка М имеет полярные координаты ρ и φ.

Обычно считают, что ρ и φ изменяются в пределах: 0<ρ<+∞, 0<φ<2 . Однако в ряде случаев рассматриваются углы, большие 2 , а также отрицательные, т. е. углы, отсчитыва­емые от полярной оси по часовой стрелке.

Пусть начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью и пусть точка М имеет прямоугольные координаты х и у и полярные координаты ρ и φ (рис. 7). Тогда переход от полярных координат точки М к прямоугольным осуществляется по формулам

х=ρ*cosφ, у=ρ*sinφ,

а выражение полярных координат через прямоугольные следует из этих формул:

ρ= ,

(1)

Пример. Даны прямоугольные координаты точки (2; 2). Найти ее полярные координаты, считая, что полюс совмещен с началом прямоугольной системы координат, а полярная ось совпадает с положительной полуосью абсцисс.

Решение. По формулам (1) имеем 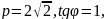откуда 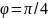или , так как 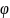изменяется от 0 до 2π. Но так как 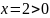и 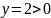, то следует взять

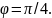
41. Построить точки, заданные полярными координатами:

А (2; π/2); В(3; π/4); С(3; Зπ/4); D(4; 0); F(2; Зπ/2) и Р(3; π).

42. Найти полярные координаты точек, симметричных относительно полярной оси точкам А (3; π/3); В(4;-π/4).

43. Найти полярные координаты точек, симметричных от­носительно полюса точкам А(1;π/4); (5;-π/З).

44. Даны точки а полярной системе координат A(2; π/4),

В(4; π/2). Найти их прямоугольные координаты,

45. Даны точки а прямоугольной системе координат 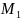(0; 5);

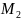(-3; 0); 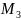( ; 1). Найти их полярные координаты.

46. Даны точки в полярной системе координат A(8;-2π/3) и В(6;π/3). Найти полярные координаты середины отрезка, соединяющего точки А и В.

47. Даны точки в полярной системе координат А(3.;π/6) и В(5; 2π/3). Найти расстояние d между ними.

48. Даны точки в полярной системе координат А( 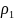; ) и В(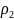 ; 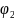). Найти расстояние d между ними.

49. Одна из вершин треугольника ОАВ находится в полюсе, две другие — точки А(5;π/4) и B(4;π/12). Найти площадь этого треугольника.

50. Найти площадь треугольника, вершины которого — точки A(3; π/8), B(8; 7π/24) и С (6; 5π/8).

51. Дана точка в полярной системе координат (10; π/6). Найти ее прямоугольные координаты, если известно, что полюс полярной системы находится в точке (2; 3), а полярная ось параллельна оси абсцисс.