Глава 3.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

§ 1.Направленные отрезки и их величины. Числовая прямая

1. Ось и отрезки. Прямая с выбранным на ней положительным направление называется осью (рис.1). Рассмотрим на оси две произвольные точки: А и В.

Определение 1. Отрезок с граничными точками А и В называется направленным, если указано, какая из точек А и В считается началом, а какая – концом отрезка.

Направленный отрезок обозначается 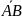², где А обозначает начало, а В - конец отрезка.

Определение 2. Величиной АВ направленного отрезка называется вещественное число, равное , если направления отрезка и оси совпадают, и равное -|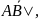 если эти направления противоположны.

Если точки А и В направленного отрезка совпадают, то величина равна нулю, а направление не определено.

Основное тождество. Для любых трёх точек А, В и С на оси величина отрезка 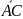равна сумме величин отрезков и А 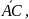т. е. АВ + ВС = АС.

2. Числовая прямая. Координатной прямой называется прямая, на которой выбрана точка, являющаяся началом отсчета, масштабный отрезок и положительное направление (она становится осью).

Пусть М – произвольная точка координатной прямой (рис. 2). Координатой точки М называется вещественное число , равное величине ОМ направленного отрезка 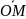: =ОМ. Число называется координатой точки М. Символ М( ) означает, что точка М имеет координату

Итак, вещественные числа изображаются координатной прямой. Поэтому множество всех вещественных чисел называют числовой прямой, а любое число – точкой этой прямой.

Если М₁ ( ) и М₂ ( ) – две произвольные точки числовой прямой, то формула

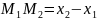
выражает величину отрезка 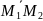, формула

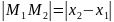
выражает его длину.

1. П остроить на числовой прямой точки А( 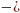5), В( + 4), С( 2) и найти величины АВ, ВС, АС отрезков АВ, ВС, и АС. Проверить что

2. Какая из двух точек правее: А(а) или В( а)?

3. Какая из двух точек правее: А(а) или В(2а)?

4. Найти величину АВ и длину отрезка , заданного точками: 1) А(3) и В(11); 2) А(5) и В(2); 3)А( 1) и В(3); 4) А( 5) и В( 3); 5) А( 1) и В( 3).

5. Вычислить координату точки А, если известны: 1) В(3) и АВ = 5; 2) В(2) и АВ = 3; 3) В( 1) и ВА = 2; 4) В( 5) и ВА = 3; 5) В(0) и 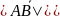= 2; 6) В(2) и = 3; 7) В( 1) и = 5; 8) В( 5) и = 2.

6. Построить на числовой прямой точки, которые удовлетворяют уравнениям:

1)

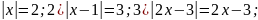
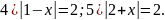
7. Охарактеризовать расположение на числовой прямой множеств точек, координаты которых удовлетворяют неравенствам:

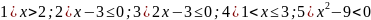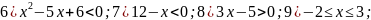
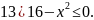; К каждому случаю сделать рисунок.

8. Охарактеризовать расположение на числовой прямой множеств точек, координаты которых удовлетворяют неравенствам:

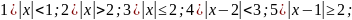
§ 2. Прямоугольная (декартова) система координат

Две взаимно перпендикулярные оси О и О , имеющие общее начало О и одинаковую единицу масштаба (рис.3), образуют прямоугольную (или декартову) систему координат на плоскости.

Ось О называется осью абсцисс, ось О осью ординат, точка О – началом координат.

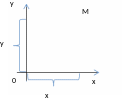
Рис.3 Рис. 4

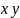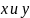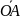Плоскость, в которой расположены оси О и О , называется координатной плоскостью и обозначается О . Пусть М – произвольная точка плоскости. Опустим из неё перпендикуляры МА и МВ на оси О и О . Прямоугольными координатами точки М называются величины ОА и ОВ направленных отрезков и

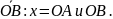
Координаты точки М называются соответственно её абсциссой и ординатой. Символ М означает, что точка М имеет координаты . Начало координат имеет координаты (0;0).

Таким образом, каждой точке М на плоскости соответствует пара чисел – её прямоугольные координаты.

Оси координат разбивают плоскость на четыре части, их называют четвертями, квадрантами или координатными углами и нумеруют римскими цифрами I,II,III,IV так, как показано на рис.4, на том же рисунке указаны так же знаки координат точек в зависимости от их расположения в той или иной четверти.

9. Постройте точки

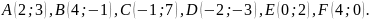
10. Не строя точку 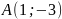, выяснить, в какой четверти она расположена.

11. В каких четвертях может находится точка, если её абсцисса положительна?

12. На оси О взята точка с координатой 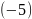. Каковы её координаты на плоскости?

13. Найти координаты точек, симметричных относительно оси О точкам:

14. Найти координаты точек, симметричных относительно оси О точкам:

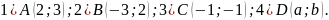
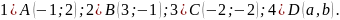
15. Найти координаты точек, симметричных относительно начала координат точкам:

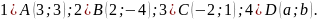
16. Найти координаты точек, симметричных относительно биссектрисы первого координатного угла точкам:

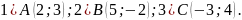
17. Найти координаты точек, симметричных относительно биссектрисы второго координатного угла точкам:

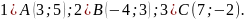
18. Дана точка М 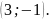Написать координаты точек, симметричных относительно оси О , оси О , начала координат биссектрисы координатного угла.

19. Определить, в каких четвертях может быть расположена точка M 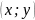, если: