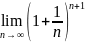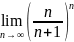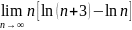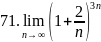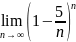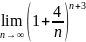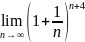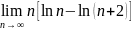- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
2. Основные свойства сходящихся последовательностей
Теорема 1. Сходящаяся последовательность ограничена.
Теорема
2.
Пусть
,
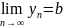 ,
тогда: а)
,
тогда: а)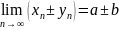 ;
б)
;
б)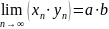 ;в)
;в)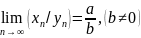 .
.
Теорема
3.
Если
,
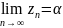 и для всех
выполняется неравенство
и для всех
выполняется неравенство
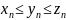 ,
то
,
то
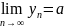 .
.
Теорема
4.
Если
и последовательность
– ограниченная, то
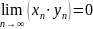 (произведение бесконечно малой на
ограниченную есть бесконечно малая).
(произведение бесконечно малой на
ограниченную есть бесконечно малая).
Найти пределы:
21. 23. 25. 27. 29. 31. 33. 35. 37.
39. 41. 43. 45. 47.
|
22. 24.
26. 28. 30. 32. 34. 36. 38. 40. 42. 44. 46.
|
§3. Монотонные последовательности
Определение монотонных последовательностей.
Определение.
Последовательность
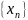 называется возрастающей, если
называется возрастающей, если
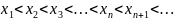 ; неубывающей, если
; неубывающей, если
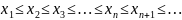 ; убывающей, если
; убывающей, если
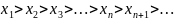 ; невозрастающей
; невозрастающей
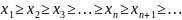 .
.
Все такие последовательности объединяются общим названием монотонные. Возрастающие и убывающие называются строго монотонными.
Пример
1.
Последовательность
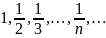 убывающая и ограниченная.
убывающая и ограниченная.
Пример
2.
Последовательность
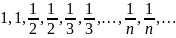 невозрастающая и ограниченная.
невозрастающая и ограниченная.
Пример
3.
Последовательность
 возрастающая и неограниченная.
возрастающая и неограниченная.
Пример
4.
Последовательность
 неубывающая и неограниченная.
неубывающая и неограниченная.
Пример
5.
Последовательность
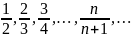 возрастающая и ограниченная.
возрастающая и ограниченная.
48.
Доказать, что последовательность с
общим элементом
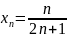 монотонно возрастающая.
монотонно возрастающая.
49.
Доказать, что последовательность с
общим элементом
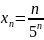 монотонно
убывающая.
монотонно
убывающая.
50.
Доказать, что последовательность
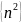 монотонно
возрастающая.
монотонно
возрастающая.
51.
Доказать, что последовательность
 }
монотонно убывающая.
}
монотонно убывающая.
52.
Доказать, что последовательность
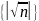 монотонно неубывающая.
монотонно неубывающая.
53.Выяснить,
монотонна ли последовательность { }
и есть ли у неё наибольший и наименьший
элементы.
}
и есть ли у неё наибольший и наименьший
элементы.
54.
Доказать, что последовательность
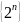 монотонно возрастающая.
монотонно возрастающая.
55. Доказать, что:
Последовательность {
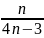 }
монотонно убывающая.
}
монотонно убывающая.Последовательность {
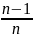 }
монотонно возрастающая.
}
монотонно возрастающая.Последовательность { } монотонно возрастающая и ограничена.
Последовательность {
 }
монотонно убывающая и ограничена.
}
монотонно убывающая и ограничена.Последовательность {
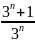 }
монотонно убывающая и ограничена.
}
монотонно убывающая и ограничена.
Признак сходимости монотонных последовательностей.
Теорема. Монотонная ограниченная последовательность имеет предел.
56. Доказать существование предела последовательности
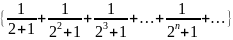 .
.
57. Доказать существование предела последовательностей:
 .
.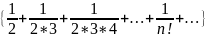 .
.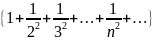 .
.
58.
Доказать, что последовательность { }
сходится, и найти её предел.
}
сходится, и найти её предел.
59.
Последовательность
задана рекуррентным соотношением
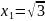 ,
,
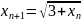 .
Доказать, что эта последовательность
сходится, и найти её предел.
.
Доказать, что эта последовательность
сходится, и найти её предел.
60.
Последовательность
задана рекуррентным соотношением
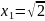 ,
,
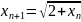 .
Доказать, что эта последовательность
сходится, и найти её предел.
.
Доказать, что эта последовательность
сходится, и найти её предел.
61.
Последовательность
задана рекуррентным соотношением
,
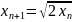 .
Доказать, что эта последовательность
сходится, и найти её предел.
.
Доказать, что эта последовательность
сходится, и найти её предел.
62.
Доказать, что последовательность {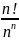 }
сходится, и найти её предел.
}
сходится, и найти её предел.
3. Число
Число
называется предел
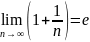 .
Это число иррационально и приближено
равно
=2,71828… . Логарифмы с основанием е
называется натуральными и обозначаются
.
Это число иррационально и приближено
равно
=2,71828… . Логарифмы с основанием е
называется натуральными и обозначаются
 .
.
Найти пределы:
63. 65.
67.
69.
|
64.
66.
68. 70.
72.
|

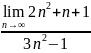 .
.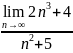 .
.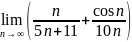 .
. .
.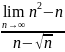 .
.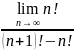 .
. .
.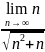 .
. .
.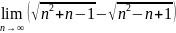 .
.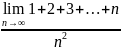 .
.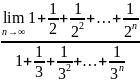 .
.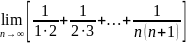 .
.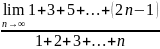 .
.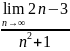 .
.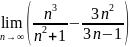 .
. .
.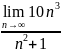 .
.
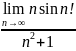 .
.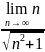 .
.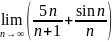 .
.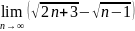 .
.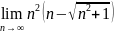 .
.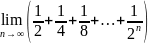 .
. .
. .
.