
- •Глава 1
- •§ 1. Основные понятия
- •§ 2. Грани числовых множеств
- •§ 3. Абсолютная величина вещественного числа
- •Глава 2
- •§1. Числовые последовательности
- •1. Определение числовой последовательности.
- •3. Бесконечно большие и бесконечно малые последовательности.
- •§2. Сходящиеся последовательности
- •Определение предела последовательности.
- •2. Основные свойства сходящихся последовательностей
- •§3. Монотонные последовательности
- •Определение монотонных последовательностей.
- •Признак сходимости монотонных последовательностей.
- •3. Число
- •Глава 3.
- •§ 1.Направленные отрезки и их величины. Числовая прямая
- •§ 2. Прямоугольная (декартова) система координат
- •§ 3. Простейшие задачи аналитической геометрии на плоскости
- •§ 4. Полярные координаты
- •§ 5. Уравнение линии как множество точек плоскости
- •§ 6. Линии первого порядка
- •Уравнение прямом с угловым коэффициентом
- •Уравнение прямой, проходящей через данную точку m( , ) с данным угловым коэффициентом:
- •Уравнение прямой, проходящей через две данные точки м1( ; ) и м2( ; ):
- •Общее уравнение прямой
- •98. Найти расстояния точек а (4; ?
- •§ 7. Смешанные задачи на прямую
- •§ 8. Линии второго порядка
- •Глава 4
- •§ 1.Основные понятия
- •§ 2. Предел и непрерывность функции
- •Свойства пределов.
- •§3. Сравнение бесконечно малых
- •Глава 5
- •§ 1. Понятие производной
- •§2. Вычисление производных
- •§3. Понятие дифференциала
- •§4. Производные и дифференциалы высших порядков
- •Глава 6
- •§ 1. Первообразная и неопределенный интеграл
- •2. Основные свойства неопределенного интеграла.
- •3. Таблица основных интегралов.
- •§2. Основные методы интегрирования
- •§4 Определённый интеграл.
- •2.Основные свойства определенного интеграла.
- •Глава 7.
- •§ 1. Определители
- •3. Свойства определителей.
- •§ 2. Исследование системы трех уравнений первой степени с тремя неизвестными
- •Глава 8
3. Бесконечно большие и бесконечно малые последовательности.
Определение 5. Последовательность { } называется бесконечно большой, если для любого положительного числа А существует номер N такой, что при n>N выполняется неравенство | |>A.
Пример 1. Используя определение 5, доказать, что последовательность {n} является бесконечно большой.
Решение.
Возьмем любое число А>0.
Из неравенства |
|=
|n|>A
получаем n>A.
Если взять N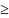 A,
то для всех n>N
будет выполняться |
|>A
т.е. последовательность {n}
бесконечно большая.
A,
то для всех n>N
будет выполняться |
|>A
т.е. последовательность {n}
бесконечно большая.
Замечание. Любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, 1, 4,…1, n, 1, n+1, … не является бесконечно большой, поскольку при A >1 неравенство | |>A не имеет места для всех элементов с нечетными номерами.
Определение
6.
Последовательность
{ }
называется бесконечно малой, если для
любого положительного числа
существует номер N
такой, что при n>N
выполняется неравенство |
|<
.
}
называется бесконечно малой, если для
любого положительного числа
существует номер N
такой, что при n>N
выполняется неравенство |
|<
.
Пример 2. Используя определение 6, доказать, что последовательность { } является бесконечно малой.
Решение.
Возьмем любое число
>0. Из неравенства |
|=|
|<
получаем n>[ ],
то для всех n>N
будет выполняться |
|<
,
т.е. последовательность {
}
бесконечно малая.
],
то для всех n>N
будет выполняться |
|<
,
т.е. последовательность {
}
бесконечно малая.
Теорема.
Если {
}
– бесконечно большая последовательность,
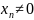 ,
то последовательность {
}=
,
то последовательность {
}=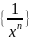 – бесконечно малая, и, обратно, если {
}
– бесконечно малая последовательность,
– бесконечно малая, и, обратно, если {
}
– бесконечно малая последовательность,
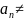 0,
то последовательность {
}=
0,
то последовательность {
}=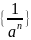 – бесконечно большая.
– бесконечно большая.
6.
Доказать, что последовательность
{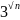 }
является
бесконечно большой.
}
является
бесконечно большой.
7.
Доказать, что последовательности: 1)
{-n};
2) {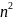 };
3){(-1
*n}
является
бесконечно большими.
};
3){(-1
*n}
является
бесконечно большими.
8.
Доказать, что последовательность
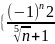 }
является бесконечно малой.
}
является бесконечно малой.
9.
Доказать, что последовательности: 1)
{
};
2) {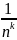 }
(k>0);
3) {
}
(k>0);
3) {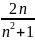 }
являются бесконечно малыми.
}
являются бесконечно малыми.
10.
Показать, что неограниченная
последовательность {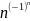 }
не является бесконечно большой.
}
не является бесконечно большой.
11.
Доказать, что последовательность {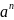 }
является: 1) бесконечно большой при
|a|>1;
}
является: 1) бесконечно большой при
|a|>1;
2) бесконечно малой при |a|<1.
§2. Сходящиеся последовательности
Определение предела последовательности.
Определение.
Число
а называется пределом последовательности
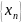 ,
если для любого положительного числа
существует номер
,
если для любого положительного числа
существует номер
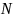 такой, что при
такой, что при
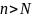 выполняется равенство
выполняется равенство
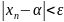
При этом последовательность называется сходящейся, в противном случае расходящейся.
Обозначение:
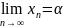 или
или
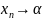 при
при
 .
.
Пример
1. Используя
определение предела, доказать, что.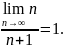
Решение.
Возьмем любое число
 Так как
Так как
 ,
то для нахождения
,
то для нахождения
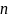 ,
удовлетворяющих
,
удовлетворяющих
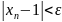 ,
достаточно решить неравенство
,
достаточно решить неравенство
 ,
откуда получим
,
откуда получим
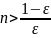 .
Если взять
.
Если взять
 ,
то для всех
будет выполняться
,
т.е.
,
то для всех
будет выполняться
,
т.е.
12.
Доказать, что
13.
Доказать, что

14.
Доказать, что: 1)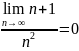 ;
2)
;
2)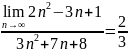 ;
3)
;
3)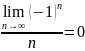 ;
4)
;
4)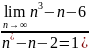 ;
5)
;
5)
15.
Известно, что
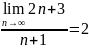 .
Найти номер
,
начиная с которого выполняется неравенство
.
Найти номер
,
начиная с которого выполняется неравенство
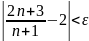 ,
где
,
где
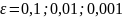 .
.
16.
Доказать, что последовательность
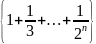 имеет своим пределом число 2.
имеет своим пределом число 2.
17.
Доказать, что последовательность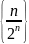 имеет своим пределом число 0.
имеет своим пределом число 0.
18.
Доказать, что
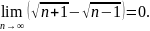
Замечание.
Если последовательность
бесконечно большая, то пишут
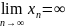 .
Если при этом начиная с некоторого
номера
все элементы положительны (отрицательны),
то пишут
.
Если при этом начиная с некоторого
номера
все элементы положительны (отрицательны),
то пишут
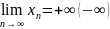 .
Говорят, что бесконечно большая
последовательность имеет бесконечный
предел.
.
Говорят, что бесконечно большая
последовательность имеет бесконечный
предел.
19.
Привести примеры последовательностей
 и
,
для которых
и
,
для которых
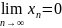 ,
,
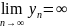 ,
а произведение из
,
а произведение из
 являлось последовательностью: а)
сходящейся; б) бесконечно малой; в)
бесконечно большой; г) расходящейся.
являлось последовательностью: а)
сходящейся; б) бесконечно малой; в)
бесконечно большой; г) расходящейся.
20.
Привести примеры таких последовательностей
и
,
что
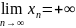 ,
,
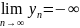 и, кроме того: 1)
и, кроме того: 1)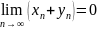 ;
2)
;
2)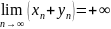 ;
3)
;
4)
;
3)
;
4) не
существует.
не
существует.
